Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục I trang 83, 84, 85 sách giáo khoa Toán 10 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Một vât dịch chuyển từ A đến B và tiếp tục dịch chuyển từ B đến C (Hình 49). Cho ABCD là hình bình hành (Hình 52). So sánh: Hãy giải thích hướng đi của thuyền ở Hình 48.
Một vât dịch chuyển từ A đến B và tiếp tục dịch chuyển từ B đến C (Hình 49).
a) Biểu diễn vecto dịch chuyển của vật từ A đến B và từ B đến C.
b) Xác định vecto dịch chuyển tổng hợp của vật
Lời giải chi tiết:
a) vecto dịch chuyển của vật từ A đến B là \(\overrightarrow {AB} \)và từ B đến C là \(\overrightarrow {BC} \)
b) Tóm lại vật đó dịch chuyển từ A đến C, vecto dịch chuyển tổng hợp của vật là \(\overrightarrow {AC} \)
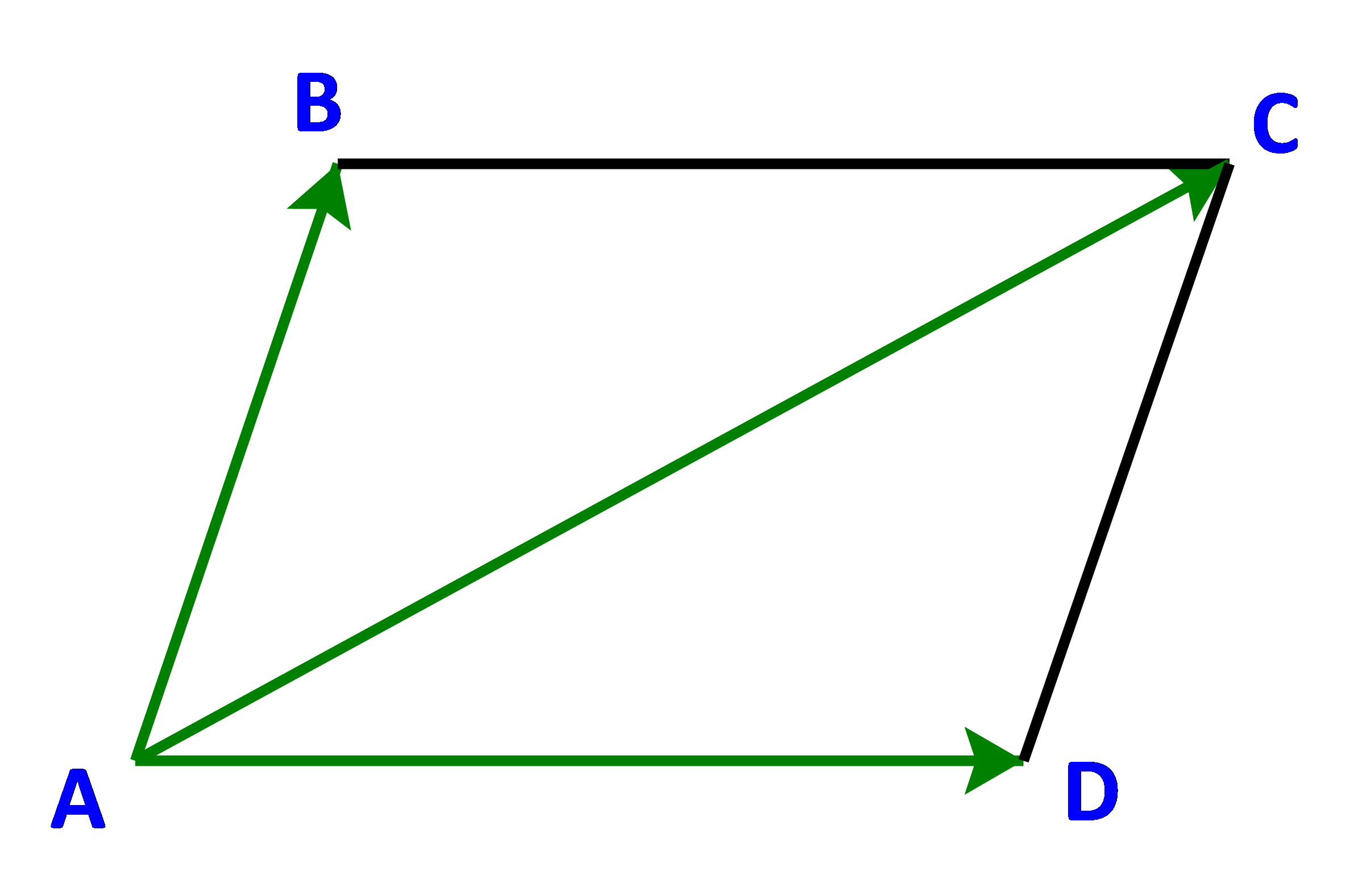
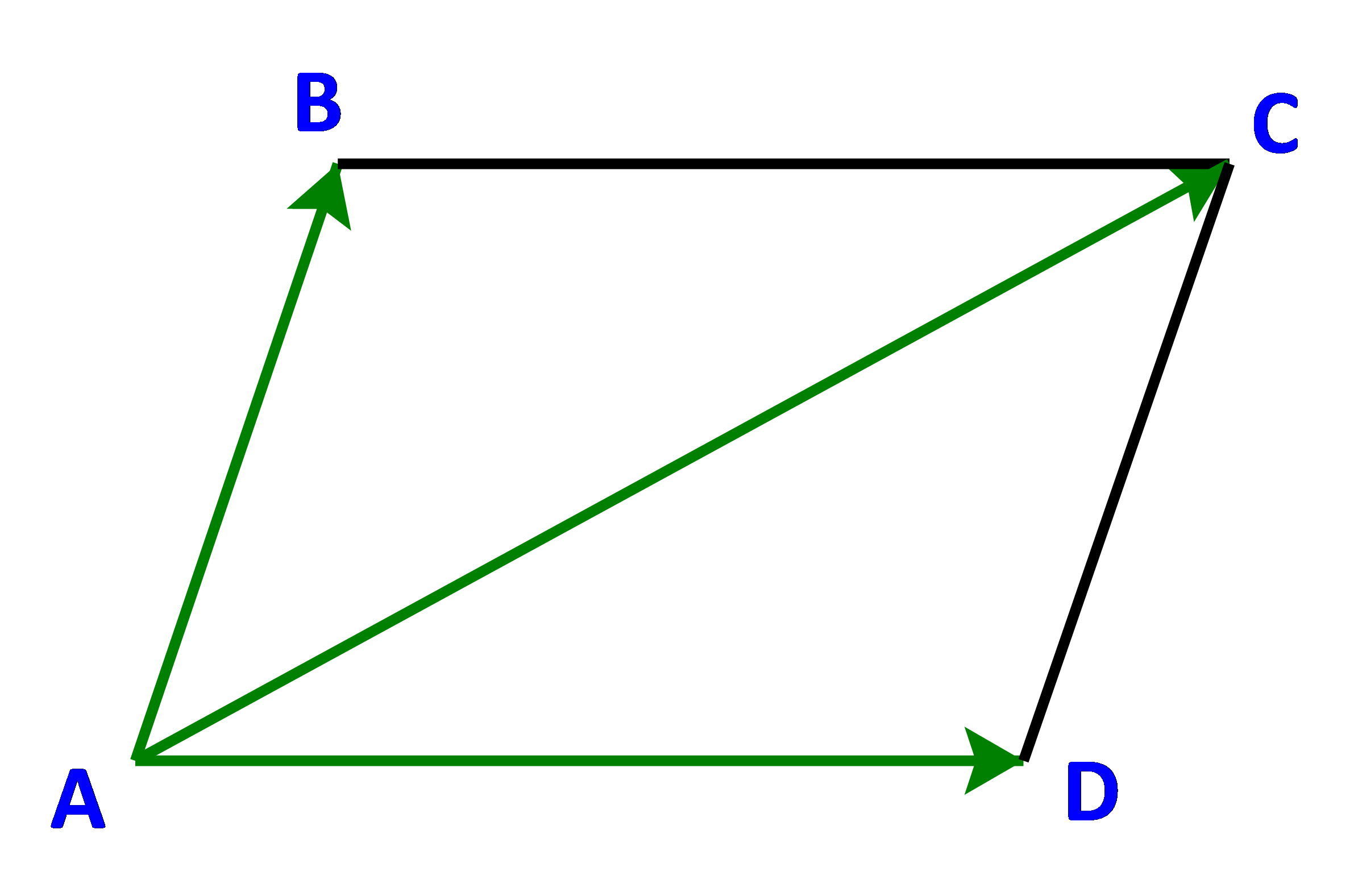
Cho ABCD là hình bình hành (Hình 52). So sánh:
a) Hai vecto \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
b) Vecto tổng \(\overrightarrow {AB} + \overrightarrow {AD} \) và vecto \(\overrightarrow {AC} \)
Phương pháp giải:
a) Nhận xét về giá, hướng và độ dài của hai vecto đó.
b) Thay vecto \(\overrightarrow {AD} \) bởi vecto \(\overrightarrow {BC} \)trong tổng rồi tính.
Lời giải chi tiết:
a) Ta có: \(\left\{ \begin{array}{l}AD//BC\\AD = BC\end{array} \right.\) (do tứ giác ABCD là hình bình hành)
\( \Rightarrow \overrightarrow {AD} = \overrightarrow {BC} \)
b) Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
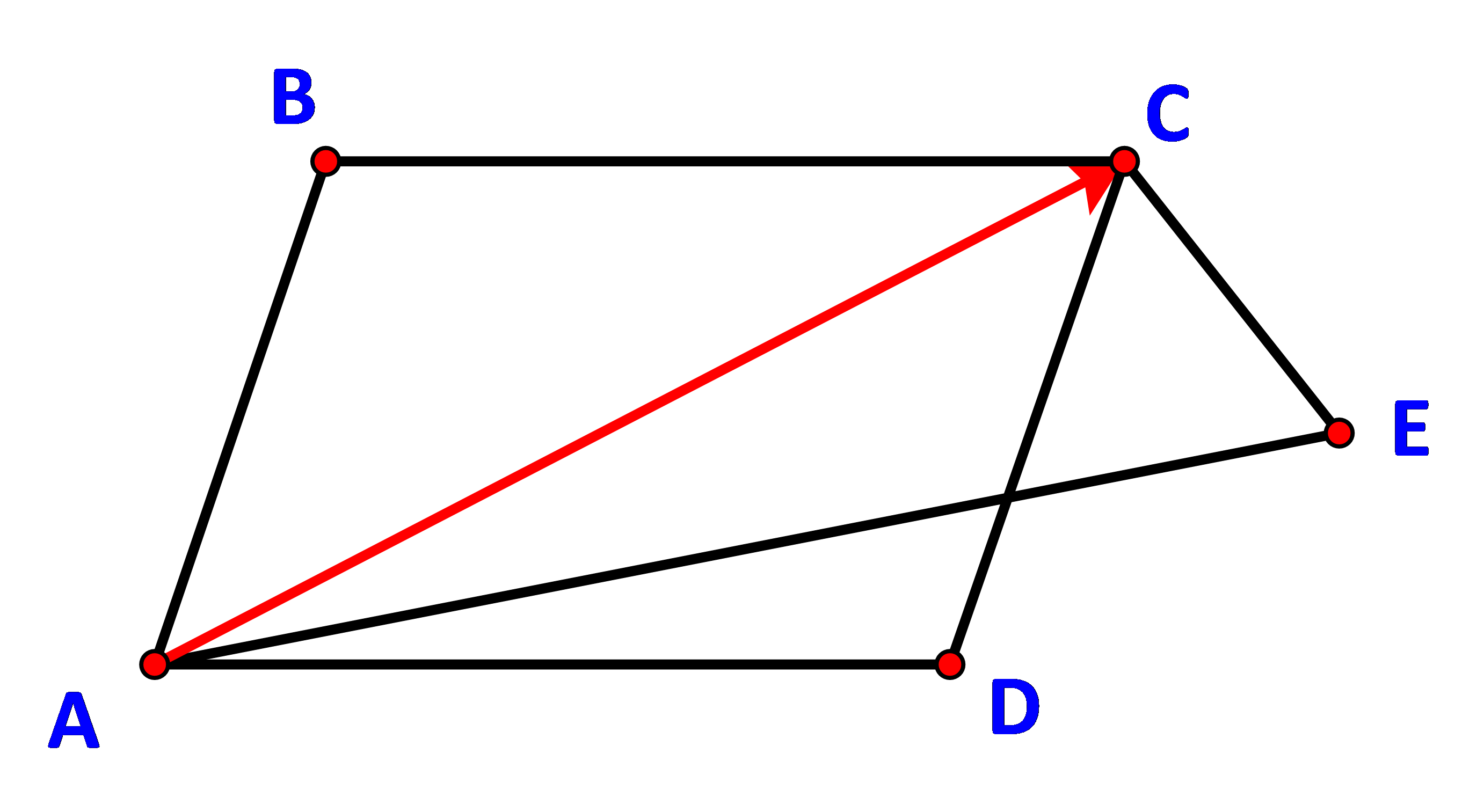
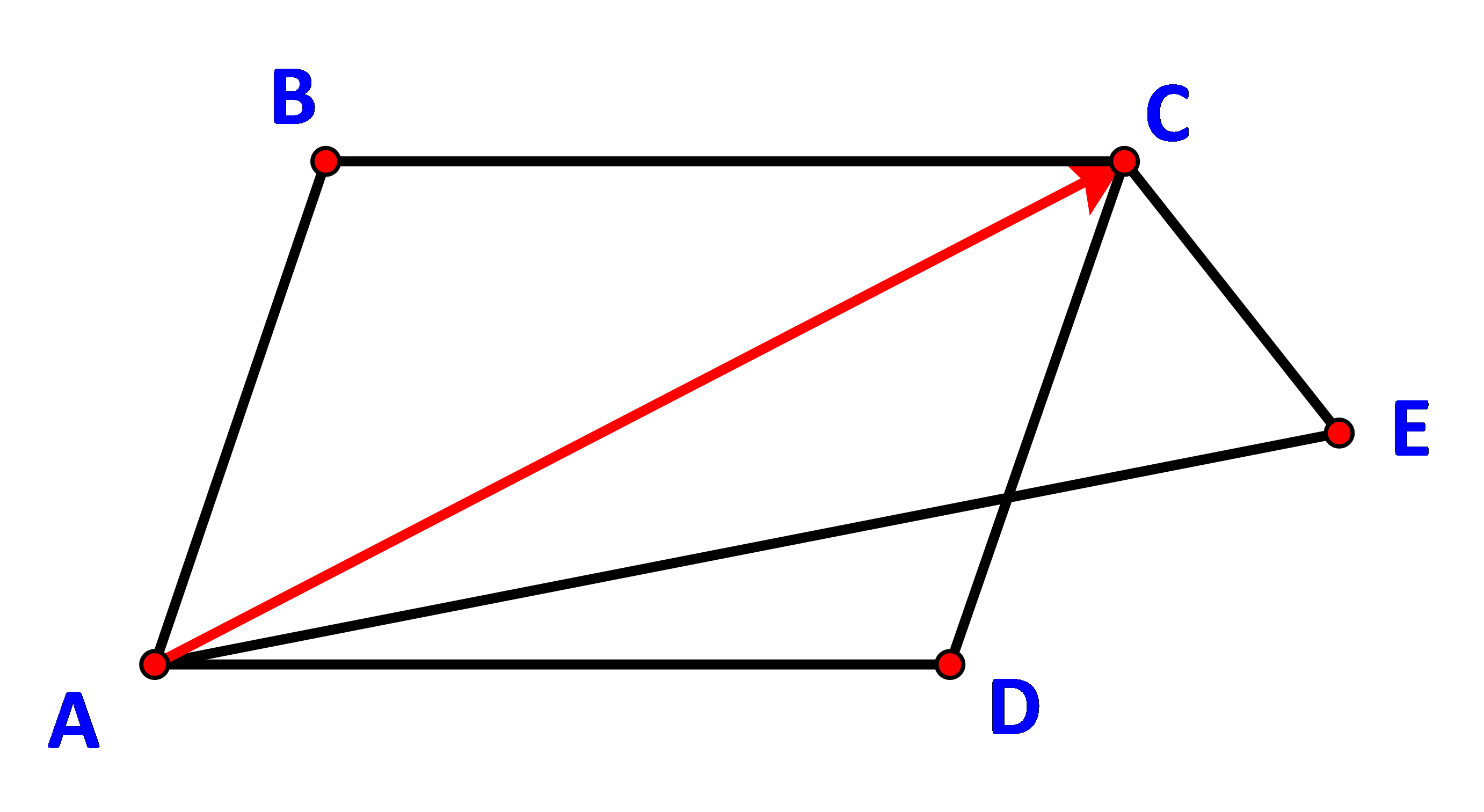
Cho hình bình hành ABCD và điểm E bất kì. Chứng minh: \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = \overrightarrow {AE} \).
Phương pháp giải:
Bước 1: Sử dụng tính chất giao hoán, ta tính: \((\overrightarrow {AB} + \overrightarrow {AD} ) + \overrightarrow {CE} \)
Bước 2: Vận dụng quy tắc hình bình hành, chỉ ra \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)từ đó suy ra đpcm.
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = (\overrightarrow {AB} + \overrightarrow {AD} ) + \overrightarrow {CE} \) (tính chất giao hoán)
Mà theo quy tắc hình bình hành ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Suy ra \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = \overrightarrow {AC} + \overrightarrow {CE} = \overrightarrow {AE} \)
Vậy \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = \overrightarrow {AE} \) với điểm E bất kì.
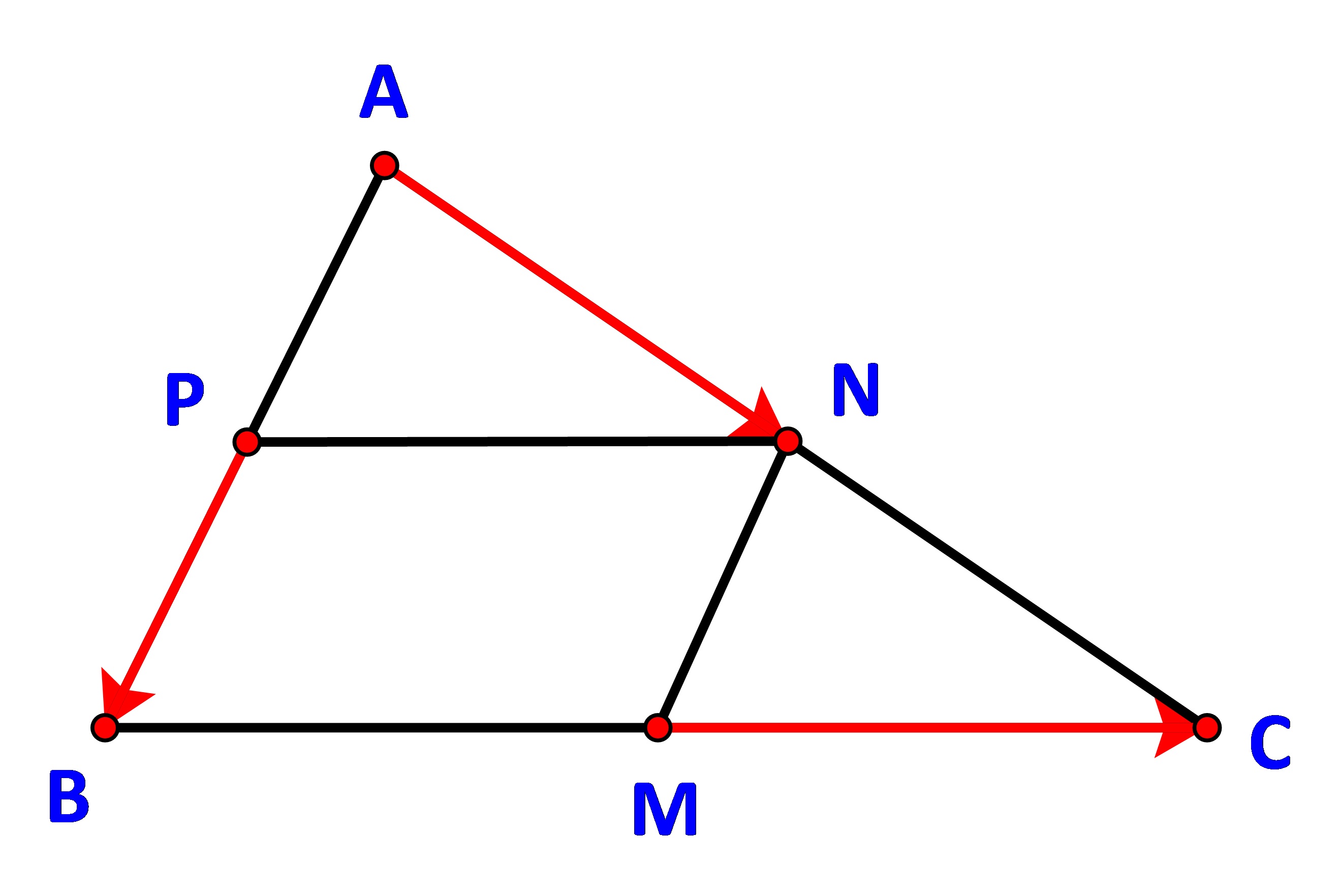
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {AN} \)
Phương pháp giải:
Bước 1: Chứng minh \(\overrightarrow {PB} = \overrightarrow {NM} ;\;\overrightarrow {AN} = \overrightarrow {NC} \)
Bước 2: Tính tổng \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {NM} + \overrightarrow {MC} = \overrightarrow {NC} = \overrightarrow {AN} \)
Lời giải chi tiết:
Do M, N, P lần lượt là trung điểm của BC, CA, AB
\( \Rightarrow MN = \frac{{AB}}{2} = PB\) và MN // PB.
\( \Rightarrow \overrightarrow {PB} = \overrightarrow {NM} \)
Ta có: \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {NM} + \overrightarrow {MC} = \overrightarrow {NC} \)
Lại có: \(\overrightarrow {NC} = \overrightarrow {AN} \) (do N là trung điểm của AC)
Vậy \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {AN} \)
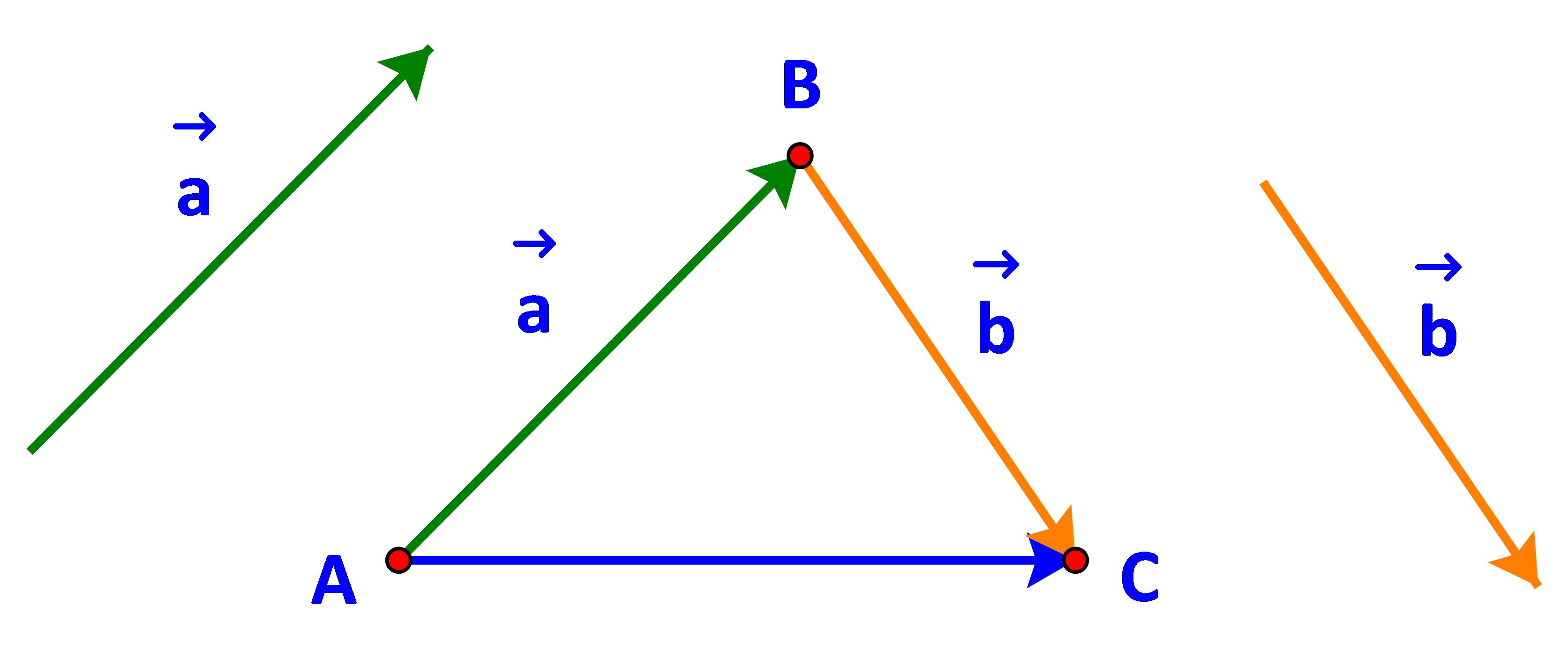
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \). Lấy một điểm A tùy ý.
a) Vẽ \(\overrightarrow {AB} = a\), \(\overrightarrow {BC} = b\)
b) Tổng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \)bằng vecto nào?
Phương pháp giải:
a) Nêu cách xác định điểm B, điểm C.
b) Xác định tổng của hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \)
Lời giải chi tiết:
a) Gọi M, N lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).
Vì \(\overrightarrow a = \overrightarrow {AB} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {AB} \) nên tứ giác MNBA là hình bình hành.
Nói cách khác B là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow a \) và điểm A.
Tương tự, C là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow b \) và điểm B.
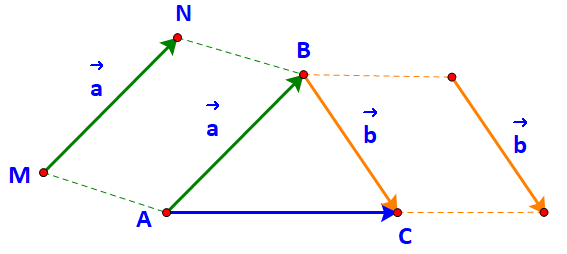
b) Dễ thấy: tổng của hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) là vecto \(\overrightarrow {AC} \).
Do đó tổng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \)bằng vecto \(\overrightarrow {AC} \).
Ta có viết: \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Hãy giải thích hướng đi của thuyền ở Hình 48.

Phương pháp giải:
Bước 1: Gọi tên các lực tác động lên thuyền.
Bước 2: Vận dụng quy tắc hình bình hành tính tổng hai lực.
Lời giải chi tiết:
Gọi vecto \(\overrightarrow {AB} ,\overrightarrow {AD} \) là các vecto biểu diễn lực mà hai người cùng tác động lên điểm A của thuyền.
Khi đó thuyền chịu một lực là tổng hai lực kéo đó.
Vậy thuyền đi theo hướng của vecto tổng \(\overrightarrow {AB} + \overrightarrow {AD} \)
Vẽ hình bình hành ABCD. Khi đo ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Vậy khi hai người cùng kéo, thuyền đi theo vecto đường chéo của hình bình hành tạo bởi hai lực kéo của hai người.
Một vât dịch chuyển từ A đến B và tiếp tục dịch chuyển từ B đến C (Hình 49).
a) Biểu diễn vecto dịch chuyển của vật từ A đến B và từ B đến C.
b) Xác định vecto dịch chuyển tổng hợp của vật
Lời giải chi tiết:
a) vecto dịch chuyển của vật từ A đến B là \(\overrightarrow {AB} \)và từ B đến C là \(\overrightarrow {BC} \)
b) Tóm lại vật đó dịch chuyển từ A đến C, vecto dịch chuyển tổng hợp của vật là \(\overrightarrow {AC} \)
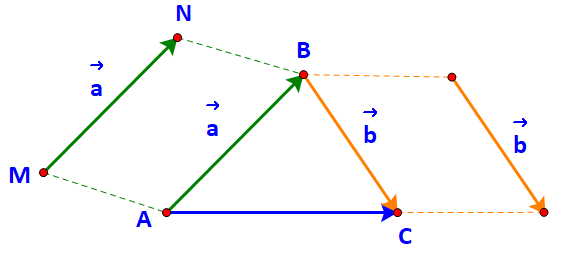
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \). Lấy một điểm A tùy ý.
a) Vẽ \(\overrightarrow {AB} = a\), \(\overrightarrow {BC} = b\)
b) Tổng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \)bằng vecto nào?
Phương pháp giải:
a) Nêu cách xác định điểm B, điểm C.
b) Xác định tổng của hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \)
Lời giải chi tiết:
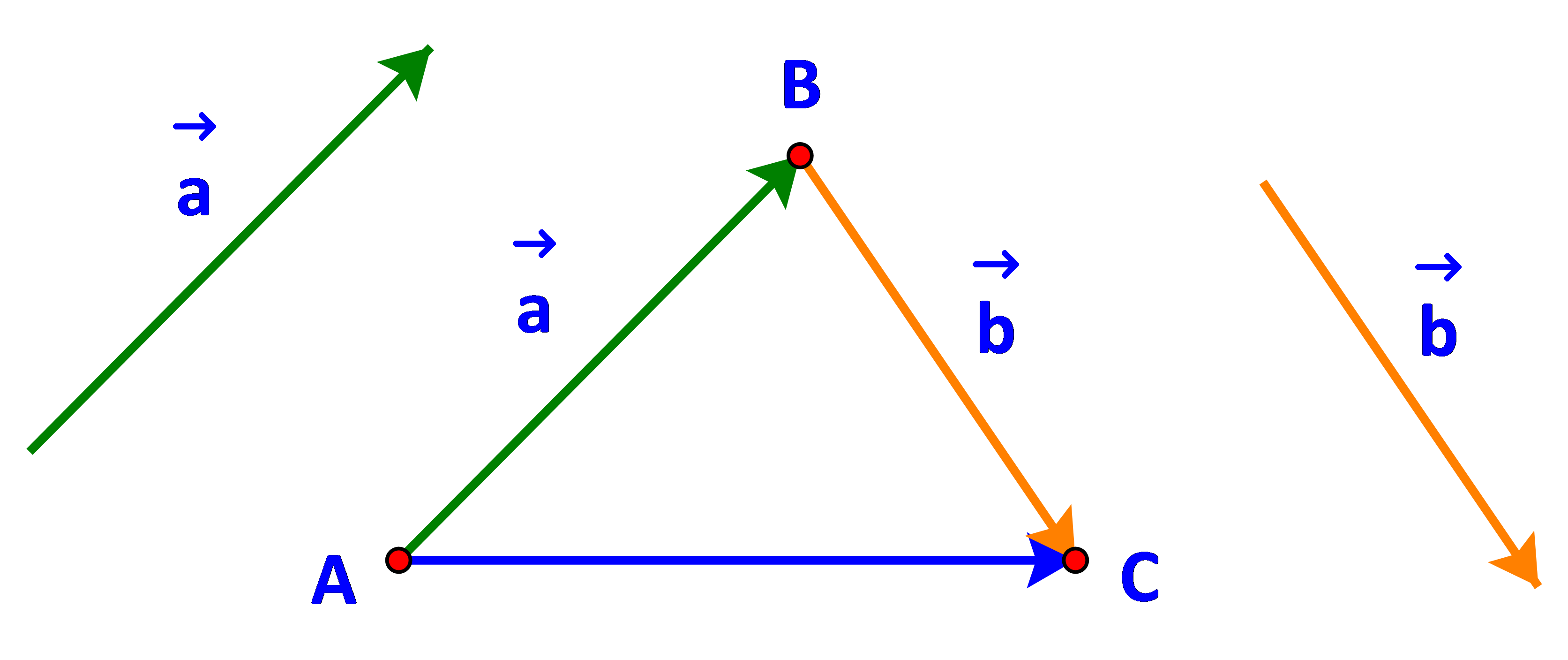
a) Gọi M, N lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).
Vì \(\overrightarrow a = \overrightarrow {AB} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {AB} \) nên tứ giác MNBA là hình bình hành.
Nói cách khác B là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow a \) và điểm A.
Tương tự, C là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow b \) và điểm B.
b) Dễ thấy: tổng của hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) là vecto \(\overrightarrow {AC} \).
Do đó tổng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \)bằng vecto \(\overrightarrow {AC} \).
Ta có viết: \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {AN} \)
Phương pháp giải:
Bước 1: Chứng minh \(\overrightarrow {PB} = \overrightarrow {NM} ;\;\overrightarrow {AN} = \overrightarrow {NC} \)
Bước 2: Tính tổng \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {NM} + \overrightarrow {MC} = \overrightarrow {NC} = \overrightarrow {AN} \)
Lời giải chi tiết:
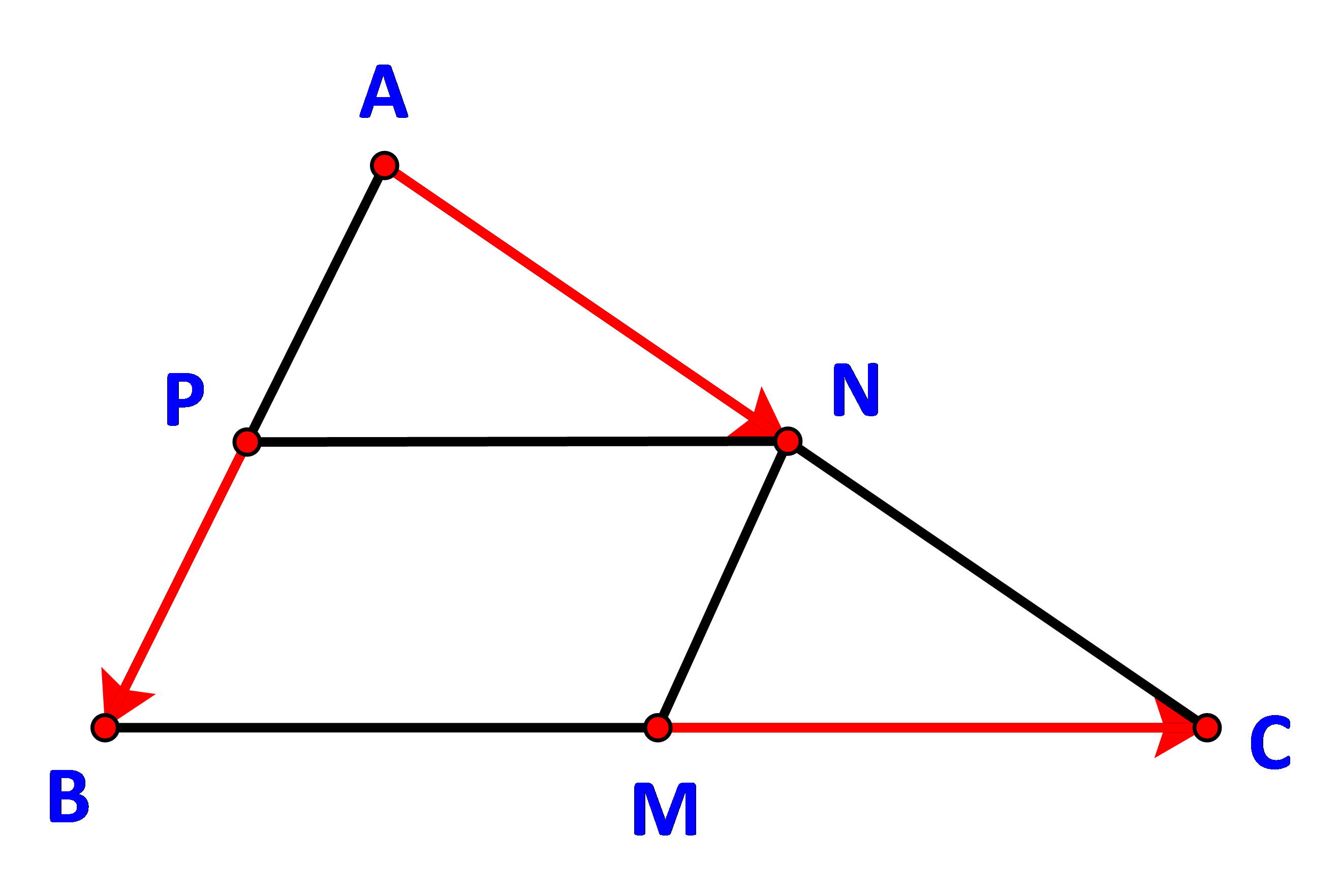
Do M, N, P lần lượt là trung điểm của BC, CA, AB
\( \Rightarrow MN = \frac{{AB}}{2} = PB\) và MN // PB.
\( \Rightarrow \overrightarrow {PB} = \overrightarrow {NM} \)
Ta có: \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {NM} + \overrightarrow {MC} = \overrightarrow {NC} \)
Lại có: \(\overrightarrow {NC} = \overrightarrow {AN} \) (do N là trung điểm của AC)
Vậy \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {AN} \)
Cho ABCD là hình bình hành (Hình 52). So sánh:
a) Hai vecto \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
b) Vecto tổng \(\overrightarrow {AB} + \overrightarrow {AD} \) và vecto \(\overrightarrow {AC} \)
Phương pháp giải:
a) Nhận xét về giá, hướng và độ dài của hai vecto đó.
b) Thay vecto \(\overrightarrow {AD} \) bởi vecto \(\overrightarrow {BC} \)trong tổng rồi tính.
Lời giải chi tiết:
a) Ta có: \(\left\{ \begin{array}{l}AD//BC\\AD = BC\end{array} \right.\) (do tứ giác ABCD là hình bình hành)
\( \Rightarrow \overrightarrow {AD} = \overrightarrow {BC} \)
b) Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Hãy giải thích hướng đi của thuyền ở Hình 48.

Phương pháp giải:
Bước 1: Gọi tên các lực tác động lên thuyền.
Bước 2: Vận dụng quy tắc hình bình hành tính tổng hai lực.
Lời giải chi tiết:
Gọi vecto \(\overrightarrow {AB} ,\overrightarrow {AD} \) là các vecto biểu diễn lực mà hai người cùng tác động lên điểm A của thuyền.
Khi đó thuyền chịu một lực là tổng hai lực kéo đó.
Vậy thuyền đi theo hướng của vecto tổng \(\overrightarrow {AB} + \overrightarrow {AD} \)
Vẽ hình bình hành ABCD. Khi đo ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Vậy khi hai người cùng kéo, thuyền đi theo vecto đường chéo của hình bình hành tạo bởi hai lực kéo của hai người.
Cho hình bình hành ABCD và điểm E bất kì. Chứng minh: \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = \overrightarrow {AE} \).
Phương pháp giải:
Bước 1: Sử dụng tính chất giao hoán, ta tính: \((\overrightarrow {AB} + \overrightarrow {AD} ) + \overrightarrow {CE} \)
Bước 2: Vận dụng quy tắc hình bình hành, chỉ ra \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)từ đó suy ra đpcm.
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = (\overrightarrow {AB} + \overrightarrow {AD} ) + \overrightarrow {CE} \) (tính chất giao hoán)
Mà theo quy tắc hình bình hành ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Suy ra \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = \overrightarrow {AC} + \overrightarrow {CE} = \overrightarrow {AE} \)
Vậy \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = \overrightarrow {AE} \) với điểm E bất kì.
Mục I trong SGK Toán 10 tập 1 - Cánh diều tập trung vào việc ôn tập chương trình Đại số lớp 9 và giới thiệu các khái niệm cơ bản về tập hợp, số thực, và các phép toán trên số thực. Đây là nền tảng quan trọng để học sinh tiếp thu các kiến thức nâng cao hơn trong chương trình Toán 10.
Bài tập này yêu cầu học sinh ôn lại các khái niệm về tập hợp, các phép toán hợp, giao, hiệu, bù của tập hợp. Các bài tập thường yêu cầu học sinh xác định các tập hợp, thực hiện các phép toán trên tập hợp, và chứng minh các đẳng thức liên quan đến tập hợp.
Bài tập này tập trung vào việc ôn lại các khái niệm về số thực, các phép toán cộng, trừ, nhân, chia trên số thực, và các tính chất của các phép toán này. Các bài tập thường yêu cầu học sinh thực hiện các phép toán trên số thực, so sánh các số thực, và giải các phương trình đơn giản.
Bài tập này giới thiệu khái niệm giá trị tuyệt đối của một số thực và các tính chất của nó. Các bài tập thường yêu cầu học sinh tính giá trị tuyệt đối của một số thực, giải các phương trình và bất phương trình chứa giá trị tuyệt đối.
| Số thực x | Giá trị tuyệt đối |x| |
|---|---|
| 3 | 3 |
| -5 | 5 |
| 0 | 0 |
Để giải các bài tập trong mục I trang 83, 84, 85 SGK Toán 10 tập 1 - Cánh diều một cách hiệu quả, học sinh cần:
Học Toán 10 đòi hỏi sự kiên trì và nỗ lực. Hãy dành thời gian ôn tập bài cũ, làm bài tập đầy đủ, và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Đừng ngại đặt câu hỏi và thảo luận để hiểu rõ hơn về các khái niệm và phương pháp giải bài tập.
Hy vọng rằng với lời giải chi tiết và các phương pháp giải bài tập hiệu quả mà chúng tôi đã cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 10. Chúc các em học tốt và đạt kết quả cao!