Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 41 SGK Toán 10 tập 2 – Cánh diều tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp các em tự tin hơn trong việc học tập môn Toán.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ các em học sinh ôn tập và làm bài tập một cách hiệu quả.
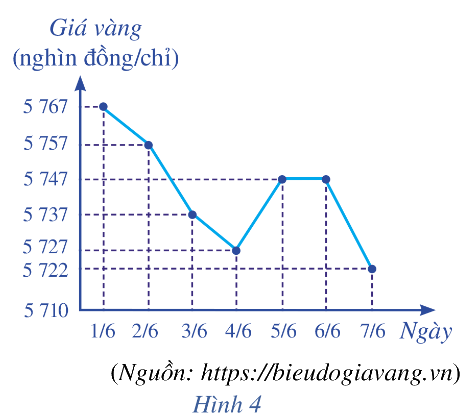
Biểu đồ đoạn thẳng ở Hình 4 biểu diễn giá vàng bán ra trong bảy ngày đầu tiên của tháng 6 năm 2021.
Đề bài
Biểu đồ đoạn thẳng ở Hình 4 biểu diễn giá vàng bán ra trong bảy ngày đầu tiên của tháng 6 năm 2021.
a) Viết mẫu số liệu thống kê giá vàng bán ra nhận được từ biểu đồ ở Hình 4.
b) Tìm khoảng biến thiên của mẫu số liệu đó.
c) Tìm khoảng tứ phân vị của mẫu số liệu đó.
d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
Phương pháp giải - Xem chi tiết
a) Quan sát biểu đồ
b) Cho mẫu số liệu: \({x_1},{x_2},...,{x_n}\)
+) Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: \({X_1},{X_2},...,{X_n}\)
+) Bước 2: Khoảng biến thiên: \(R = {X_n} - {X_1}\)
c) +) Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: \({X_1},{X_2},...,{X_n}\)
+) Bước 2: \({Q_2} = {M_e} = \left\{ \begin{array}{l}{X_{k + 1}}\quad \quad \quad \quad \quad (n = 2k + 1)\\\frac{1}{2}({X_k} + {X_{k + 1}})\quad \;\,(n = 2k)\end{array} \right.\)
\({Q_1}\) là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
\({Q_3}\) là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
d) +) Tính phương sai \({s^2} = \frac{1}{n}\left[ {{{\left( {{x_1} - \overline x } \right)}^2} + {{\left( {{x_2} - \overline x } \right)}^2} + ... + {{\left( {{x_n} - \overline x } \right)}^2}} \right]\)
+) Độ lệch chuẩn \(s = \sqrt {{s^2}} \)
Lời giải chi tiết
a) Dựa vào biểu đồ, ta có mẫu số liệu là:
5767 5757 5737 5727 5747 5747 5722
b) Khoảng biến thiên của mẫu số liệu đó là: \(R = {x_{\max }} - {x_{\min }} = 5767 - 5722 = 45\).
c)
+) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
5722 5727 5737 5747 5747 5757 5767
+) Các tứ phân vị của mẫu số liệu là:
Trung vị của mẫu số liệu: \({Q_2}\) = 5747.
Trung vị của dãy 5722 5727 5737 là: \({Q_1}\) = 5727.
Trung vị của dãy 5747 5757 5767 là: \({Q_3}\) = 5757.
+) Khoảng tứ phân vị của mẫu số liệu là: \({\Delta _Q} ={Q_3} - {Q_1}\) = 5757 - 5727 = 30.
d)
+) Giá vàng trung bình trong 7 ngày đầu tiên của tháng 6 năm 2021 là: \(\overline x = \frac{{5722{\rm{ + }}5727{\rm{ + }}5737{\rm{ + }}5747{\rm{ + }}5747{\rm{ + }}5757{\rm{ + }}5767}}{7} = 5743,43\) (nghìn đồng/chỉ).
+) Phương sai của mẫu số liệu là: \({s^2} = \frac{{\left[ {{{\left( {5722 - \overline x } \right)}^2} + {{\left( {5727 - \overline x } \right)}^2} + ... + {{\left( {5767 - \overline x } \right)}^2}} \right]}}{7} \approx 219,39\).
+) Độ lệch chuẩn của của mẫu số liệu là: \(s = \sqrt {{s^2}} = \sqrt {219,39} \approx 14,81\) (nghìn đồng/chỉ).
Bài 3 trang 41 SGK Toán 10 tập 2 – Cánh diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất liên quan.
Bài 3 trang 41 SGK Toán 10 tập 2 – Cánh diều thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi trong bài.
(Nội dung câu a và lời giải chi tiết)
(Nội dung câu b và lời giải chi tiết)
(Nội dung câu c và lời giải chi tiết)
Để giải các bài tập về vectơ một cách hiệu quả, các em học sinh cần lưu ý những điều sau:
Ví dụ 1: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng AB + AC = 2AM.
Lời giải:
Ta có: AM = AB + BM. Vì M là trung điểm của BC nên BM = MC. Do đó, BC = 2BM. Suy ra BM = 1/2 BC. Vậy AM = AB + 1/2 BC. Tương tự, AC = AM + MC = AM + BM = AM + 1/2 BC. Cộng hai phương trình trên, ta được AB + AC = 2AM + BC. Tuy nhiên, điều này không đúng. Cách giải đúng:
AB + AC = 2AM. Thật vậy, theo quy tắc hình bình hành, AB + AC = AD, với D là đỉnh thứ tư của hình bình hành ABCD. Vì M là trung điểm của BC nên M cũng là trung điểm của AD. Do đó, AM = 1/2 AD = 1/2 (AB + AC). Suy ra AB + AC = 2AM.
Để củng cố kiến thức về vectơ, các em học sinh có thể làm thêm các bài tập sau:
Hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả mà chúng tôi đã trình bày, các em học sinh sẽ tự tin hơn trong việc giải bài 3 trang 41 SGK Toán 10 tập 2 – Cánh diều và các bài tập tương tự. Chúc các em học tập tốt!