Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục III trang 89, 90 SGK Toán 10 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài tập mục III tập trung vào các kiến thức về vectơ, phép toán vectơ và ứng dụng của vectơ trong hình học.
Cho tam giác ABC có G là trọng tâm. Chứng minh Cho ba điểm phân biệt A, B, C. Ở hình 61, tìm k trong mỗi trường hợp sau:
Cho tam giác ABC có G là trọng tâm. Chứng minh \(\overrightarrow {AB} + \overrightarrow {AC} = 3\overrightarrow {AG} .\)
Phương pháp giải:
G là trọng tâm tam giác ABC thì \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \) với điểm M bất kì.
Lời giải chi tiết:
Với điểm M bất kì ta có: \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
Chọn M trùng A, ta được: \(\overrightarrow {AA} + \overrightarrow {AB} + \overrightarrow {AC} = 3\overrightarrow {AG} \Leftrightarrow \overrightarrow {AB} + \overrightarrow {AC} = 3\overrightarrow {AG} .\)
Cho ba điểm phân biệt A, B, C.
a) Nếu ba điểm A, B, C thẳng hàng thì hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương hay không?
b) Ngược lại, nếu hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương thì ba điểm A, B, C có thẳng hàng hay không?
Phương pháp giải:
Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Lời giải chi tiết:
a) Nếu A, B, C thẳng hàng thì đường thẳng AB trùng đường thẳng AC, do đó hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương.
b) Nếu hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương thì đường thẳng AB trùng đường thẳng AC, do đó ba điểm A, B, C có thẳng hàng.
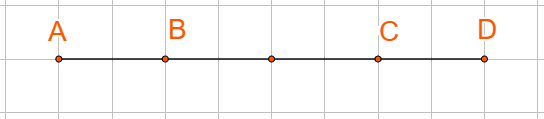
Ở hình 61, tìm k trong mỗi trường hợp sau:
a) \(\overrightarrow {AC} = k.\overrightarrow {AD} \)
b) \(\overrightarrow {BD} = k.\overrightarrow {DC} \)
Phương pháp giải:
Từ hình vẽ suy ra hướng và tỉ số độ dài của hai vecto.
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {AC} ,\overrightarrow {AD} \)là hai vecto cùng hướng và \(\left| {\overrightarrow {AC} } \right| = \frac{3}{4}\left| {\overrightarrow {AD} } \right|\)
Suy ra \(\overrightarrow {AC} = \frac{3}{4}\overrightarrow {AD} .\) Vậy \(k = \frac{3}{4}.\)
b) Ta có: \(\overrightarrow {BD} ,\overrightarrow {DC} \)là hai vecto ngược hướng và \(\left| {\overrightarrow {BD} } \right| = 3\left| {\overrightarrow {DC} } \right|\)
Suy ra \(\overrightarrow {BD} = - 3\overrightarrow {DC} .\) Vậy \(k = - 3.\)
Cho tam giác ABC có G là trọng tâm. Chứng minh \(\overrightarrow {AB} + \overrightarrow {AC} = 3\overrightarrow {AG} .\)
Phương pháp giải:
G là trọng tâm tam giác ABC thì \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \) với điểm M bất kì.
Lời giải chi tiết:
Với điểm M bất kì ta có: \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
Chọn M trùng A, ta được: \(\overrightarrow {AA} + \overrightarrow {AB} + \overrightarrow {AC} = 3\overrightarrow {AG} \Leftrightarrow \overrightarrow {AB} + \overrightarrow {AC} = 3\overrightarrow {AG} .\)
Cho ba điểm phân biệt A, B, C.
a) Nếu ba điểm A, B, C thẳng hàng thì hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương hay không?
b) Ngược lại, nếu hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương thì ba điểm A, B, C có thẳng hàng hay không?
Phương pháp giải:
Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Lời giải chi tiết:
a) Nếu A, B, C thẳng hàng thì đường thẳng AB trùng đường thẳng AC, do đó hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương.
b) Nếu hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương thì đường thẳng AB trùng đường thẳng AC, do đó ba điểm A, B, C có thẳng hàng.
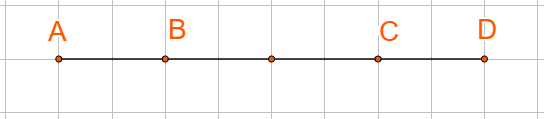
Ở hình 61, tìm k trong mỗi trường hợp sau:
a) \(\overrightarrow {AC} = k.\overrightarrow {AD} \)
b) \(\overrightarrow {BD} = k.\overrightarrow {DC} \)
Phương pháp giải:
Từ hình vẽ suy ra hướng và tỉ số độ dài của hai vecto.
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {AC} ,\overrightarrow {AD} \)là hai vecto cùng hướng và \(\left| {\overrightarrow {AC} } \right| = \frac{3}{4}\left| {\overrightarrow {AD} } \right|\)
Suy ra \(\overrightarrow {AC} = \frac{3}{4}\overrightarrow {AD} .\) Vậy \(k = \frac{3}{4}.\)
b) Ta có: \(\overrightarrow {BD} ,\overrightarrow {DC} \)là hai vecto ngược hướng và \(\left| {\overrightarrow {BD} } \right| = 3\left| {\overrightarrow {DC} } \right|\)
Suy ra \(\overrightarrow {BD} = - 3\overrightarrow {DC} .\) Vậy \(k = - 3.\)
Mục III trong SGK Toán 10 tập 1 - Cánh diều tập trung vào việc củng cố và mở rộng kiến thức về vectơ, bao gồm các phép toán cơ bản như cộng, trừ vectơ, nhân vectơ với một số thực, và ứng dụng của vectơ trong việc giải quyết các bài toán hình học phẳng. Việc nắm vững các khái niệm và kỹ năng này là nền tảng quan trọng cho việc học tập các chương trình toán học ở các lớp trên.
Mục III bao gồm các bài tập rèn luyện kỹ năng về:
Để tìm vectơ tổng của hai vectơ \vec{a}" và \vec{b}", ta sử dụng quy tắc hình bình hành hoặc quy tắc tam giác. Vectơ tổng \vec{a} + \vec{b}" có điểm đầu là điểm đầu của \vec{a}" và điểm cuối là điểm cuối của \vec{b}" (hoặc ngược lại). Tương tự, vectơ hiệu \vec{a} - \vec{b}" có điểm đầu là điểm đầu của \vec{a}" và điểm cuối là điểm cuối của \vec{b}".
Khi nhân một vectơ \vec{a}" với một số thực k", ta được một vectơ mới k\vec{a}". Vectơ k\vec{a}" có cùng phương với \vec{a}", cùng chiều với \vec{a}" nếu k > 0", ngược chiều với \vec{a}" nếu k < 0", và độ dài bằng |k|" lần độ dài của \vec{a}".
Để chứng minh các tính chất hình học bằng vectơ, ta thường sử dụng các tính chất của phép cộng, trừ vectơ, phép nhân vectơ với một số thực, và các điều kiện để hai vectơ cùng phương, cùng chiều, bằng nhau. Ví dụ, để chứng minh rằng bốn điểm A, B, C, D là bốn đỉnh của một hình bình hành, ta có thể chứng minh rằng \vec{AB} = \vec{DC}" hoặc \vec{AD} = \vec{BC}".
Ngoài SGK Toán 10 tập 1 - Cánh diều, các em có thể tham khảo thêm các tài liệu sau để nắm vững kiến thức về vectơ:
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải các bài tập mục III trang 89, 90 SGK Toán 10 tập 1 - Cánh diều. Chúc các em học tập tốt!