Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 4 trang 60 SGK Toán 10 tập 1 – Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn tự tin hơn trong việc chinh phục môn Toán.
Quan sát đồ thị hàm số bậc hai
Đề bài
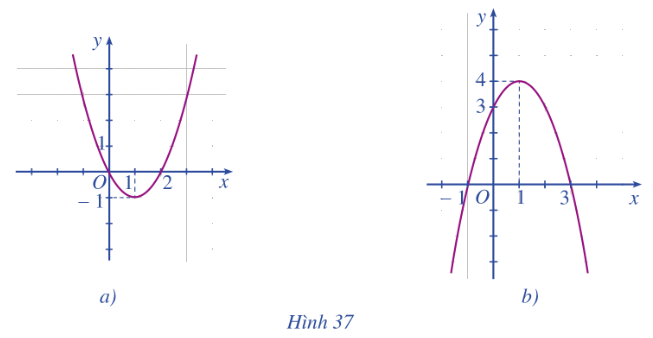
Quan sát đồ thị hàm số bậc hai \(y = a{x^2} + bx + c\) ở Hình 37a và Hình 37b rồi nêu:
a) Dấu của hệ số a;
b) Toạ độ đỉnh và trục đối xứng;
c) Khoảng đồng biến;
d) Khoảng nghịch biến;
e) Khoảng giá trị x mà y > 0;
g) Khoảng giá trị x mà \(y \le 0\).
Phương pháp giải - Xem chi tiết
a) Xác định bề lõm và so sánh a với 0
b) Xác định đỉnh và trục đối xứng của mỗi đồ thị.
c) Quan sát đồ thị và tìm khoảng đồng biến
d) Quan sát đồ thị và tìm khoảng nghịch biến
e) Khoảng giá trị x mà đồ thị nằm trên trục Ox
g) Khoảng giá trị x mà đồ thị nằm dưới trục Ox
Lời giải chi tiết
a)
Hình 37a: Bề lõm hướng lên trên nên a>0
Hình 37b: Bề lõm xuống nên a<0
b)
Hình 37a: Đỉnh là (1;-1), trục đối xứng x=1
Hình 37b: Đỉnh là (1;4), trục đối xứng x=1
c)
Hình 37a: Hàm số đồng biến trên \(\left( {1; + \infty } \right)\)
Hình 37b: Hàm số đồng biến trên \(\left( { - \infty ;1} \right)\)
d)
Hình 37a: Hàm số nghịch biến trên \(\left( { - \infty ;1} \right)\)
Hình 37b: Hàm số nghịch biến trên \(\left( {1; + \infty } \right)\)
e)
Hình 37a: Đồ thị nằm trên trục Ox khi \(x \in \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\)
=> Khoảng giá trị x mà y > 0 là \(\left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\)
Hình 37b: Đồ thị nằm trên trục Ox khi \(x \in \left( { - 1;3} \right)\)
=> Khoảng giá trị x mà y > 0 là \(\left( { - 1;3} \right)\)
g)
Hình 37a: Đồ thị nằm dưới trục Ox khi \(x \in \left[ {0;2} \right]\)
=> Khoảng giá trị x mà y < 0 là \(\left[ {0;2} \right]\)
Hình 37b: Đồ thị nằm dưới trục Ox khi \(x \in \left( { - \infty ; - 1} \right] \cup \left[ {3; + \infty } \right)\)
=> Khoảng giá trị x mà \(y \le 0\) là \(\left( { - \infty ; - 1} \right] \cup \left[ {3; + \infty } \right)\)
Bài 4 trang 60 SGK Toán 10 tập 1 – Cánh diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của chúng.
Bài 4 trang 60 SGK Toán 10 tập 1 – Cánh diều thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 4 trang 60 SGK Toán 10 tập 1 – Cánh diều, chúng tôi sẽ cung cấp lời giải chi tiết cho từng phần của bài tập. (Ở đây sẽ là nội dung giải chi tiết từng phần của bài tập, ví dụ:)
Vectơ tổng của a và b được tính như sau:
a + b = (1 + (-3); 2 + 4) = (-2; 6)
Vectơ tích của k và c được tính như sau:
k * c = (2 * 5; 2 * (-1)) = (10; -2)
Khi giải các bài tập về vectơ, bạn cần lưu ý những điều sau:
Để củng cố kiến thức về vectơ, bạn có thể tham khảo các bài tập tương tự sau:
Bài 4 trang 60 SGK Toán 10 tập 1 – Cánh diều là một bài tập quan trọng giúp bạn hiểu rõ hơn về vectơ và các phép toán trên vectơ. Hy vọng rằng với lời giải chi tiết và các lưu ý trên, bạn sẽ tự tin hơn trong việc giải quyết bài tập này và các bài tập tương tự khác.
Hãy tiếp tục luyện tập và khám phá thêm nhiều kiến thức thú vị khác về môn Toán tại giaitoan.edu.vn!