Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục I trang 35 và 36 sách giáo khoa Toán 10 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Kết quả của 11 lần đo được thống kê trong mẫu số liệu sau: a) Tìm hiệu giữa số đo lớn nhất và số đo nhỏ nhất.
Kết quả của 11 lần đo được thống kê trong mẫu số liệu sau:
2 5 16 8 7 9 10 12 14 11 6 (1)
a) Tìm hiệu giữa số đo lớn nhất và số đo nhỏ nhất.
b) Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần. Tìm các giá trị \({Q_1},{Q_2},{Q_3}\) là tứ phân vị của mẫu đó. Sau đó, tìm hiệu \({Q_3} - {Q_1}\)
Lời giải chi tiết:
a) Trong mẫu số liệu (1), hiệu giữa số đo lớn nhất và số đo nhỏ nhất là
\(R = {x_{\max }} - {x_{\min }} = 16 - 14 = 2\)
b) +) Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần, ta được:
2 5 6 7 8 9 10 11 12 14 16
+) Vậy \({Q_1}{\rm{ }} = 6;{\rm{ }}{Q_2}{\rm{ }} = {\rm{ }}9;{\rm{ }}{Q_3}{\rm{ }} = {\rm{ }}12\) . Suy ra \({Q_3} - {Q_1}{\rm{ = }}12{\rm{ }} - 6 = 6\)
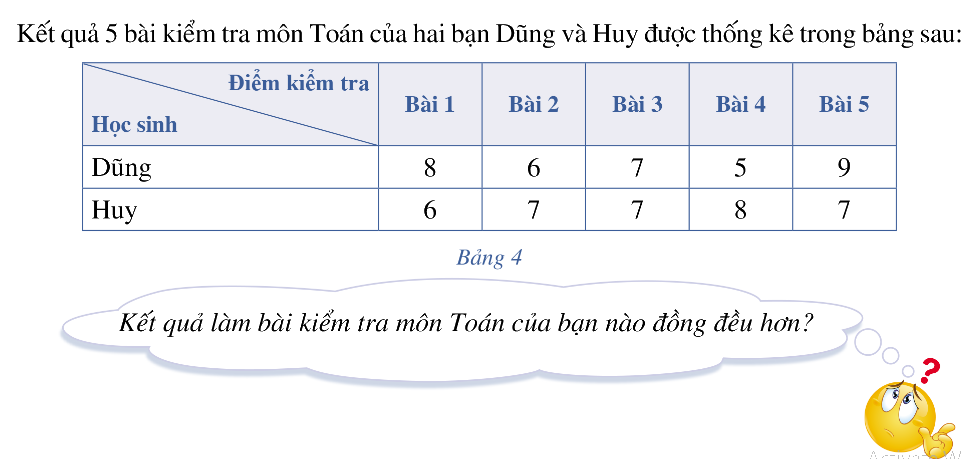
Lời giải chi tiết:
Kết quả kiểm tra toán của bạn Huy đồng đều hơn
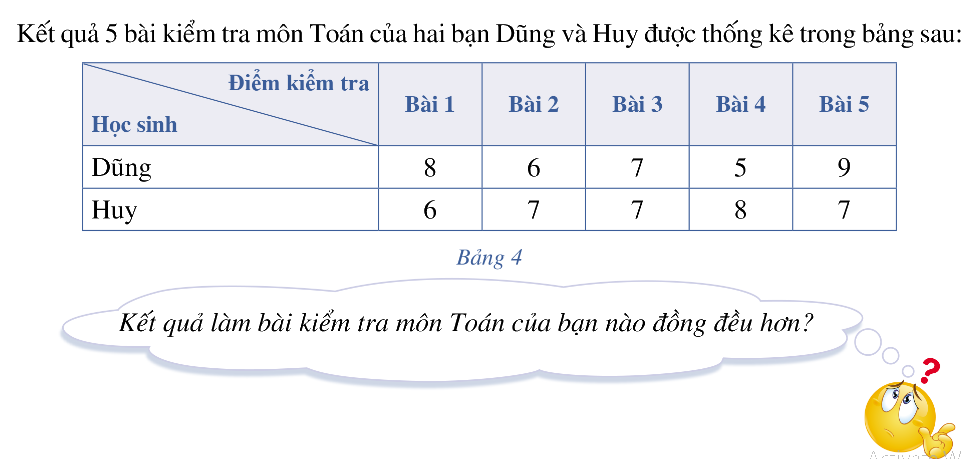
Lời giải chi tiết:
Kết quả kiểm tra toán của bạn Huy đồng đều hơn
Kết quả của 11 lần đo được thống kê trong mẫu số liệu sau:
2 5 16 8 7 9 10 12 14 11 6 (1)
a) Tìm hiệu giữa số đo lớn nhất và số đo nhỏ nhất.
b) Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần. Tìm các giá trị \({Q_1},{Q_2},{Q_3}\) là tứ phân vị của mẫu đó. Sau đó, tìm hiệu \({Q_3} - {Q_1}\)
Lời giải chi tiết:
a) Trong mẫu số liệu (1), hiệu giữa số đo lớn nhất và số đo nhỏ nhất là
\(R = {x_{\max }} - {x_{\min }} = 16 - 14 = 2\)
b) +) Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần, ta được:
2 5 6 7 8 9 10 11 12 14 16
+) Vậy \({Q_1}{\rm{ }} = 6;{\rm{ }}{Q_2}{\rm{ }} = {\rm{ }}9;{\rm{ }}{Q_3}{\rm{ }} = {\rm{ }}12\) . Suy ra \({Q_3} - {Q_1}{\rm{ = }}12{\rm{ }} - 6 = 6\)
Mục I trong SGK Toán 10 tập 2 - Cánh diều tập trung vào việc ôn tập chương trình đại số và hình học đã học. Các bài tập trong mục này thường mang tính tổng hợp, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã được trang bị để giải quyết vấn đề. Việc nắm vững các khái niệm cơ bản, công thức và phương pháp giải toán là yếu tố then chốt để hoàn thành tốt các bài tập này.
Bài tập này yêu cầu học sinh ôn lại kiến thức về hàm số bậc hai, bao gồm:
Để giải các bài tập trong bài này, học sinh cần nắm vững các công thức và phương pháp sau:
Bài tập này tập trung vào việc ôn tập về phương trình đường thẳng, bao gồm:
Để giải các bài tập trong bài này, học sinh cần nắm vững các công thức và phương pháp sau:
Bài tập này yêu cầu học sinh ôn lại kiến thức về hệ phương trình bậc nhất hai ẩn, bao gồm:
Để giải các bài tập trong bài này, học sinh cần nắm vững các bước thực hiện của từng phương pháp giải.
| Công thức | Mô tả |
|---|---|
| Tọa độ đỉnh của parabol y = ax2 + bx + c | x0 = -b/2a, y0 = (4ac - b2)/4a |
| Khoảng cách từ điểm M(x0, y0) đến đường thẳng Ax + By + C = 0 | d = |Ax0 + By0 + C| / √(A2 + B2) |
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục I trang 35, 36 SGK Toán 10 tập 2 - Cánh diều. Chúc các em học tập tốt!