Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải các bài tập trong mục III trang 69 và 70 của sách giáo khoa Toán 10 tập 1, chương trình Cánh diều.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải một cách cẩn thận, kèm theo các giải thích rõ ràng để giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Cho tam giác ABC nội tiếp đường tròn (O) có bán kính R = 6 và có các góc B = 65, C = 85 Tính độ dài cạnh BC.
Cho tam giác ABC nội tiếp đường tròn (O) có bán kính R = 6 và có các góc \(\widehat B = {65^o},\widehat C = {85^o}.\) Tính độ dài cạnh BC.
Phương pháp giải:
Bước 1: Tính góc \(\widehat A\)
Bước 2: Áp dụng định lí sin trong tam giác ABC: \(\frac{{BC}}{{\sin A}} = 2R\)
Lời giải chi tiết:
Ta có: \(\widehat B = {65^o},\widehat C = {85^o}.\)
\( \Rightarrow \widehat A = {180^o} - \left( {{{65}^o} + {{85}^o}} \right) = {30^o}.\)
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{BC}}{{\sin A}} = 2R \Rightarrow BC = 2R.\sin A\)
Mà \(\widehat A = {30^o},R = 6.\)
\( \Rightarrow BC = 2.6.\sin {30^o} = 6.\)
Vậy BC = 6.
Cho \(\alpha \) là góc vuông. Chứng minh \(\frac{a}{{\sin \alpha }} = 2R.\)
Phương pháp giải:
Bước 1: Xác định đường tròn ngoài tiếp tam giác, từ đó suy ra bán kính R
Bước 2: Tính \(\frac{a}{{\sin \alpha }}\) rồi so sánh với 2R.
Lời giải chi tiết:
Xét tam giác ABC có \(\widehat A = \alpha = {90^o}\)
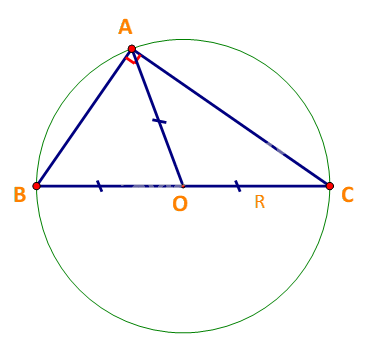
Gọi O là trung điểm của BC. Khi đó: \(OA = OB = OC = \frac{1}{2}BC\)
Do đó đường tròn ngoại tiếp tam giác ABC là (O) bán kính \(R = \frac{{BC}}{2}\)
\( \Rightarrow \frac{a}{{\sin \alpha }} = \frac{{BC}}{{\sin {{90}^o}}} = BC = 2R\) (đpcm)
Cho \(\alpha \) là góc vuông. Chứng minh \(\frac{a}{{\sin \alpha }} = 2R.\)
Phương pháp giải:
Bước 1: Xác định đường tròn ngoài tiếp tam giác, từ đó suy ra bán kính R
Bước 2: Tính \(\frac{a}{{\sin \alpha }}\) rồi so sánh với 2R.
Lời giải chi tiết:
Xét tam giác ABC có \(\widehat A = \alpha = {90^o}\)
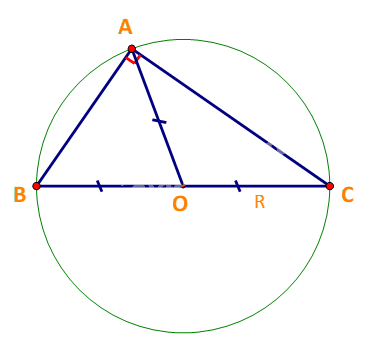
Gọi O là trung điểm của BC. Khi đó: \(OA = OB = OC = \frac{1}{2}BC\)
Do đó đường tròn ngoại tiếp tam giác ABC là (O) bán kính \(R = \frac{{BC}}{2}\)
\( \Rightarrow \frac{a}{{\sin \alpha }} = \frac{{BC}}{{\sin {{90}^o}}} = BC = 2R\) (đpcm)
Cho tam giác ABC nội tiếp đường tròn (O) có bán kính R = 6 và có các góc \(\widehat B = {65^o},\widehat C = {85^o}.\) Tính độ dài cạnh BC.
Phương pháp giải:
Bước 1: Tính góc \(\widehat A\)
Bước 2: Áp dụng định lí sin trong tam giác ABC: \(\frac{{BC}}{{\sin A}} = 2R\)
Lời giải chi tiết:
Ta có: \(\widehat B = {65^o},\widehat C = {85^o}.\)
\( \Rightarrow \widehat A = {180^o} - \left( {{{65}^o} + {{85}^o}} \right) = {30^o}.\)
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{BC}}{{\sin A}} = 2R \Rightarrow BC = 2R.\sin A\)
Mà \(\widehat A = {30^o},R = 6.\)
\( \Rightarrow BC = 2.6.\sin {30^o} = 6.\)
Vậy BC = 6.
Mục III trong SGK Toán 10 tập 1 - Cánh diều tập trung vào việc ứng dụng các kiến thức về vectơ trong hình học phẳng. Cụ thể, các bài tập trong mục này thường liên quan đến việc xác định tọa độ của vectơ, thực hiện các phép toán vectơ (cộng, trừ, nhân với một số thực), và sử dụng vectơ để chứng minh các tính chất hình học.
Bài tập này yêu cầu học sinh xác định tọa độ của một vectơ dựa trên tọa độ của các điểm đầu và điểm cuối của vectơ. Để giải bài tập này, bạn cần nắm vững công thức:
Nếu A(xA, yA) và B(xB, yB) thì vectơ AB có tọa độ là (xB - xA, yB - yA).
Ví dụ: Cho A(1, 2) và B(3, 4). Tìm tọa độ của vectơ AB.
Giải: Vectơ AB có tọa độ là (3 - 1, 4 - 2) = (2, 2).
Bài tập này yêu cầu học sinh thực hiện các phép toán cộng, trừ vectơ, và nhân vectơ với một số thực. Để giải bài tập này, bạn cần nắm vững các quy tắc sau:
Ví dụ: Cho vectơ a = (1, 2) và vectơ b = (3, 4). Tính vectơ a + b và 2a.
Giải:
a + b = (1 + 3, 2 + 4) = (4, 6)
2a = (2 * 1, 2 * 2) = (2, 4)
Bài tập này yêu cầu học sinh sử dụng vectơ để chứng minh các tính chất hình học như chứng minh hai đường thẳng song song, chứng minh hai tam giác bằng nhau, hoặc chứng minh một điểm nằm trên một đường thẳng. Để giải bài tập này, bạn cần nắm vững các kiến thức về vectơ và các tính chất hình học liên quan.
Ví dụ: Cho tam giác ABC. Chứng minh rằng nếu AB = AC thì tam giác ABC cân tại A.
Giải:
Ta có AB = AC, suy ra |AB| = |AC|. Điều này có nghĩa là độ dài của hai cạnh AB và AC bằng nhau. Do đó, tam giác ABC cân tại A.
| Công thức | Mô tả |
|---|---|
| Tọa độ của vectơ AB | (xB - xA, yB - yA) |
| Phép cộng vectơ | (x1, y1) + (x2, y2) = (x1 + x2, y1 + y2) |
| Phép nhân vectơ với một số thực | k(x, y) = (kx, ky) |
Hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, bạn đã có thể giải thành công các bài tập trong mục III trang 69, 70 SGK Toán 10 tập 1 - Cánh diều. Chúc bạn học tập tốt!