Chào mừng bạn đến với bài học về Tích của một số với một vecto trong chương trình Toán 10 Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về phép toán này, giúp bạn giải quyết các bài tập một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất, và các ứng dụng thực tế của tích một số với một vecto. Giaitoan.edu.vn cam kết mang đến cho bạn trải nghiệm học tập trực tuyến tốt nhất.
A. Lý thuyết 1. Định nghĩa
A. Lý thuyết
1. Định nghĩa
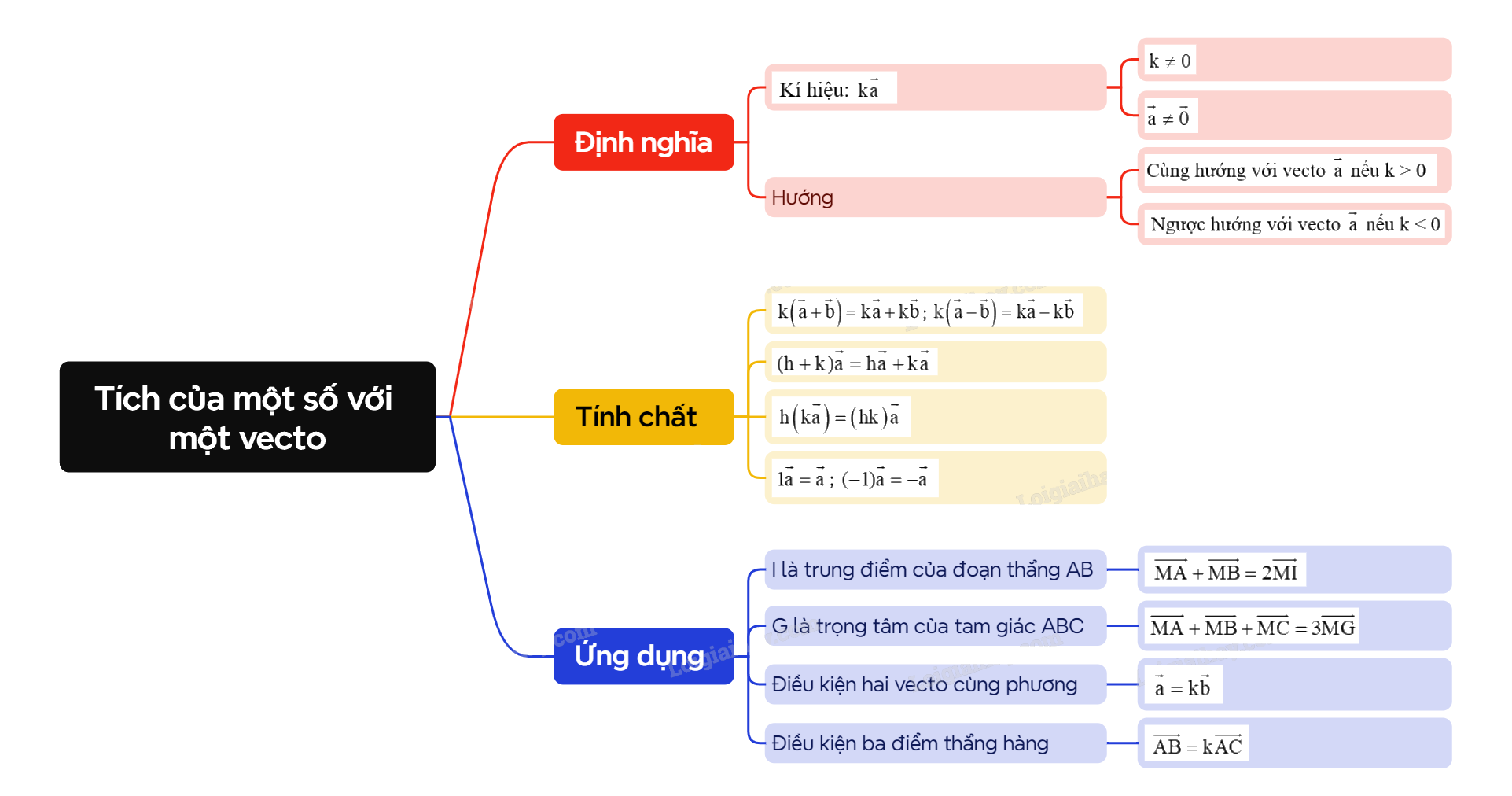
Cho số thực \(k \ne 0\) và vecto \(\overrightarrow a \ne \overrightarrow 0 \). Tích của số k với vecto \(\overrightarrow a \) là một vecto, kí hiệu là \(k\overrightarrow a \), được xác định như sau: +) Cùng hướng với vecto \(\overrightarrow a \) nếu k > 0, ngược hướng với vecto \(\overrightarrow a \) nếu k < 0. +) Có độ dài bằng \(\left| k \right|.\left| {\overrightarrow a } \right|\). |
Quy ước: \(0\overrightarrow a = \overrightarrow 0 \), \(k\overrightarrow 0 = \overrightarrow 0 \).
Phép lấy tích của một số với một vecto gọi là phép nhân một số với một vecto.
2. Tính chất
Với hai vecto bất kì \(\overrightarrow a ,\overrightarrow b \) và hai số thực h, k, ta có: +) \(k\left( {\overrightarrow a + \overrightarrow b } \right) = k\overrightarrow a + k\overrightarrow b \); \(k\left( {\overrightarrow a - \overrightarrow b } \right) = k\overrightarrow a - k\overrightarrow b \) +) \((h + k)\overrightarrow a = h\overrightarrow a + k\overrightarrow a \) +) \(h\left( {k\overrightarrow a } \right) = \left( {hk} \right)\overrightarrow a \) +) \(1\overrightarrow a = \overrightarrow a \); \(( - 1)\overrightarrow a = - \overrightarrow a \) |
Nhận xét: \(k\overrightarrow a = \overrightarrow 0 \) khi và chỉ khi k = 0 hoặc \(\overrightarrow a = \overrightarrow 0 \).
3. Một số ứng dụng
a) Trung điểm của đoạn thẳng
| Nếu I là trung điểm của đoạn thẳng AB thì \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \) với điểm M bất kì. |
b) Trọng tâm của tam giác
| Nếu G là trọng tâm của tam giác ABC thì \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \) với điểm M bất kì. |
c) Điều kiện để hai vecto cùng phương. Điều kiện để ba điểm thẳng hàng
Điều kiện cần và đủ để hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) \(\left( {\overrightarrow b \ne \overrightarrow 0 } \right)\) cùng phương là có một số thực k để \(\overrightarrow a = k\overrightarrow b \). Điều kiện cần và đủ để ba điểm A, B, C thẳng hàng là có số thực k để \(\overrightarrow {AB} = k\overrightarrow {AC} \). |
Nhận xét: Trong mặt phẳng, cho hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương. Với mỗi vecto \(\overrightarrow c \) có duy nhất cặp số (x;y) thỏa mãn \(\overrightarrow c = x\overrightarrow a + y\overrightarrow b \).
B. Bài tập
Bài 1: Cho B là trung điểm của đoạn thẳng AC. Tìm số k trong mỗi trường hợp sau:
a) \(\overrightarrow {CA} = k\overrightarrow {CB} \).
b) \(\overrightarrow {CA} = k\overrightarrow {AB} \).
Giải:
a) Ta có \(\overrightarrow {CA} ,\overrightarrow {CB} \) là hai vecto cùng hướng và \(\left| {\overrightarrow {CA} } \right| = 2\left| {\overrightarrow {CB} } \right|\).
Suy ra \(\overrightarrow {CA} = 2\overrightarrow {CB} \). Vậy k = 2.
b) Ta có \(\overrightarrow {CA} ,\overrightarrow {AB} \) là hai vecto ngược hướng và \(\left| {\overrightarrow {CA} } \right| = 2\left| {\overrightarrow {AB} } \right|\).
Suy ra \(\overrightarrow {CA} = - 2\overrightarrow {AB} \). Vậy k = -2.
Bài 2: Vật chuyển động thẳng đều từ A đến B với tốc độ là 9 m/s và vật thứ hai chuyển động thẳng đều từ B đến A với tốc độ là 6 m/s. Gọi \(\overrightarrow {{v_1}} \), \(\overrightarrow {{v_2}} \) lần lượt là các vecto vận tốc của vật thứ nhất và vật thứ hai. Có hay không số thực k thỏa mãn \(\overrightarrow {{v_1}} = k\overrightarrow {{v_2}} \)?
Giải:
Do tỉ số tốc độ của vật thứ nhất và vật thứ hai là \(\frac{9}{6} = \frac{3}{2}\) đồng thời hai vật chuyển động ngược hướng nên hai vecto vận tốc ngược hướng.
Suy ra \(\overrightarrow {{v_1}} = \frac{{ - 3}}{2}\overrightarrow {{v_2}} \). Vậy \(k = - \frac{3}{2}\).
Bài 3: Cho ba điểm A, B, C. Chứng minh:
a) \(2\overrightarrow {AB} + 2\overrightarrow {BC} = 2\overrightarrow {AC} \).
b) \(3\left( {5\overrightarrow {AC} } \right) + \overrightarrow {CB} - 14\overrightarrow {AC} = \overrightarrow {AB} \).
Giải:
a) Ta có: \(2\overrightarrow {AB} + 2\overrightarrow {BC} = 2\left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) = 2\overrightarrow {AC} \).
b) Ta có:
\(3\left( {5\overrightarrow {AC} } \right) + \overrightarrow {CB} - 14\overrightarrow {AC} = 15\overrightarrow {AC} + \overrightarrow {CB} - 14\overrightarrow {AC} = 15\overrightarrow {AC} - 14\overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \).
Bài 4: Cho tứ giác ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD. Gọi G là trung điểm của đoạn thẳng MN. Chứng minh \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
Giải:
Vì M là trung điểm của AB nên \(\overrightarrow {GA} + \overrightarrow {GB} = 2\overrightarrow {GM} \).
Vì N là trung điểm của CD nên \(\overrightarrow {GC} + \overrightarrow {GD} = 2\overrightarrow {GN} \).
Suy ra \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = 2\overrightarrow {GM} + 2\overrightarrow {GN} = 2\left( {\overrightarrow {GM} + \overrightarrow {GN} } \right) = \overrightarrow 0 \).
Bài 5: Cho tam giác OAB. Điểm M thuộc cạnh AB sao cho \(AM = \frac{2}{3}AB\). Kẻ MH // OB, MK // OA. Giả sử \(\overrightarrow {OA} = \overrightarrow a \), \(\overrightarrow {OB} = \overrightarrow b \).
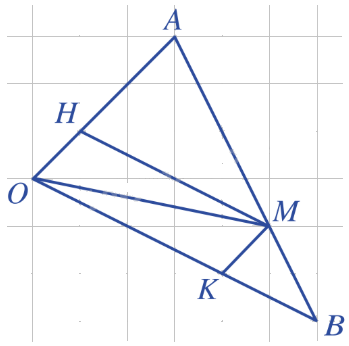
a) Biểu thị \(\overrightarrow {OH} \) theo \(\overrightarrow a \) và \(\overrightarrow {OK} \) theo \(\overrightarrow b \).
b) Biểu thị \(\overrightarrow {OM} \) theo \(\overrightarrow a \) và \(\overrightarrow b \).
Giải:
a) Ta có: MK // OA, MH // OB suy ra \(\frac{{OK}}{{OB}} = \frac{{AM}}{{AB}} = \frac{2}{3}\), \(\frac{{OH}}{{OA}} = \frac{{BM}}{{AB}} = \frac{1}{3}\).
Vì \(\overrightarrow {OH} \) và \(\overrightarrow {OA} \) cùng hướng nên \(\overrightarrow {OH} = \frac{1}{3}\overrightarrow {OA} = \frac{1}{3}\overrightarrow a \).
Vì \(\overrightarrow {OK} \) và \(\overrightarrow {OB} \) cùng hướng nên \(\overrightarrow {OK} = \frac{2}{3}\overrightarrow {OB} = \frac{2}{3}\overrightarrow b \).
b) Vì tứ giác OHMK là hình bình hành nên \(\overrightarrow {OM} = \overrightarrow {OH} + \overrightarrow {OK} = \frac{1}{3}\overrightarrow a + \frac{2}{3}\overrightarrow b \).
Trong chương trình Toán 10, phần hình học vectơ đóng vai trò quan trọng trong việc xây dựng nền tảng cho các kiến thức toán học nâng cao hơn. Một trong những khái niệm cơ bản và thiết yếu của phần này là tích của một số với một vectơ. Bài viết này sẽ trình bày chi tiết lý thuyết về tích của một số với một vectơ theo chương trình SGK Toán 10 Cánh diều, kèm theo các ví dụ minh họa và bài tập để bạn đọc có thể hiểu rõ hơn về khái niệm này.
Cho vectơ a và một số thực k. Tích của số k với vectơ a, ký hiệu là k.a, là một vectơ được xác định như sau:
Nói cách khác, k.a = k(x, y) = (kx, ky) với a = (x, y).
Phép nhân một số với một vectơ tuân theo các tính chất sau:
Ví dụ 1: Cho vectơ a = (2, 3) và số thực k = -2. Tính k.a.
Giải:
k.a = -2.(2, 3) = (-4, -6)
Ví dụ 2: Cho các vectơ a = (1, -1) và b = (0, 2) và số thực m = 3. Tính m.(a + b).
Giải:
a + b = (1, -1) + (0, 2) = (1, 1)
m.(a + b) = 3.(1, 1) = (3, 3)
Tích của một số với một vectơ có nhiều ứng dụng trong toán học và vật lý, bao gồm:
Để củng cố kiến thức về tích của một số với một vectơ, bạn có thể thực hiện các bài tập sau:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về tích của một số với một vectơ trong chương trình Toán 10 Cánh diều. Chúc bạn học tập tốt!