Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải các bài tập trong mục II trang 50, 51 sách giáo khoa Toán 10 tập 1 - Cánh diều.
Chúng tôi cam kết cung cấp nội dung chính xác, đầy đủ và giúp bạn nắm vững kiến thức Toán học một cách hiệu quả.
a) Lập bảng xét dấu của tam thức bậc hai Giải các bất phương trình bậc hai sau: Giải mỗi bất phương trình bậc hai sau bằng cách sử dụng đồ thị:
Giải các bất phương trình bậc hai sau:
a) \(3{x^2} - 2x + 4 \le 0\)
b) \( - {x^2} + 6x - 9 \ge 0\)
Phương pháp giải:
Giải bất phương trình dạng \(f\left( x \right) > 0\).
Bước 1: Xác định dấu của hệ số a và tìm nghiệm của \(f\left( x \right)\)(nếu có)
Bước 2: Sử dụng định lí về dấu của tam thức bậc hai để tìm tập hợp những giá trị của x sao cho \(f\left( x \right)\) mang dấu “+”
Bước 3: Các bất phương trình bậc hai có dạng \(f\left( x \right) < 0,f\left( x \right) \ge 0,f\left( x \right) \le 0\) được giải bằng cách tương tự.
Lời giải chi tiết:
a) Ta có \(a = 3 > 0\) và tam thức bậc hai \(f\left( x \right) = 3{x^2} - 2x + 4\) có \(\Delta ' = {1^2} - 3.4 = - 11 < 0\)
=> \(f\left( x \right) = 3{x^2} - 2x + 4\) vô nghiệm.
=> \(3{x^2} - 2x + 4 > 0\forall x \in \mathbb{R}\)
b) Ta có: \(a = - 1 < 0\) và \(\Delta ' = {3^2} - \left( { - 1} \right).\left( { - 9} \right) = 0\)
=> \(f\left( x \right) = - {x^2} + 6x - 9\) có nghiệm duy nhất \(x = 3\).
=> \( - {x^2} + 6x - 9 < 0\forall x \in \mathbb{R}\backslash \left\{ 3 \right\}\)
a) Lập bảng xét dấu của tam thức bậc hai \(f\left( x \right) = {x^2} - x - 2\)
b) Giải bất phương trình \({x^2} - x - 2 > 0\)
Phương pháp giải:
a) Tìm nghiệm của phương trình \({x^2} - x - 2 = 0\), xét hệ số và lập bảng xét dấu.
b) Dựa vào bảng xét dấu, lấy các khoảng để \(f\left( x \right) > 0\)
Lời giải chi tiết:
a) Ta có tam thức bậc hai \(f\left( x \right) = {x^2} - x - 2\) có 2 nghiệm phân biệt \({x_1} = - 1,{x_2} = 2\) và hệ số \(a = 1 > 0\)
Ta có bảng xét dấu f(x) như sau:

Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)\)b) Từ bảng xét dấu ta thấy \(f\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}x < - 1\\x > 2\end{array} \right.\)
Giải mỗi bất phương trình bậc hai sau bằng cách sử dụng đồ thị:
a) \({x^2} + 2x + 2 > 0\)
b) \( - 3{x^2} + 2x - 1 > 0\)
Phương pháp giải:
Bước 1: Vẽ đồ thị biểu diễn các hàm số.
Bước 2: Quan sát đồ thị và lấy các giá trị tương ứng với bất phương trình.
Lời giải chi tiết:
a) Ta có đồ thị:
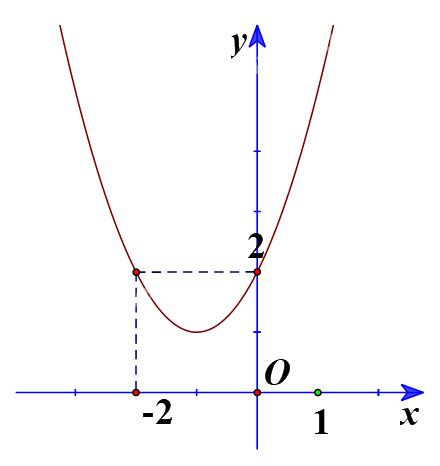
Từ đồ thị ta thấy \({x^2} + 2x + 2 > 0\) biểu diễn phần parabol \(y = {x^2} + 2x + 2\) nằm phía trên trục hoành, tương ứng với mọi \(x \in \mathbb{R}\).
Vậy tập nghiệm của bất phương trình \({x^2} + 2x + 2 > 0\) là \(\mathbb{R}\).
b) Ta có đồ thị:
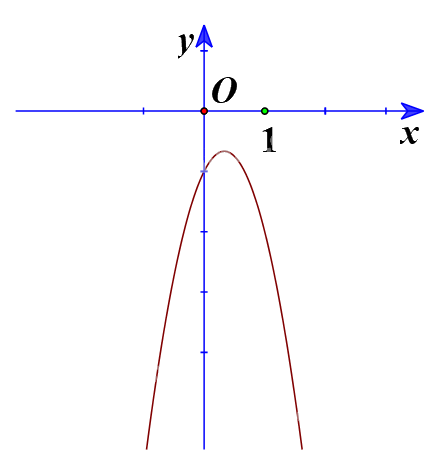
Từ đồ thị ta thấy \( - 3{x^2} + 2x - 1 > 0\) biểu diễn phần parabol \(y = - 3{x^2} + 2x - 1\) nằm phía trên trục hoành, tương ứng với \(x \in \emptyset \)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 2x - 1 > 0\) là \(\emptyset \).
Cho bất phương trình \({x^2} - 4x + 3 > 0\left( 2 \right)\).

Quan sát parabol \(\left( P \right):{x^2} - 4x + 3\) ở Hình 26 và cho biết:
a) Bất phương trình (2) biểu diễn phần parabol (P) nằm ở phía nào của trục hoành.
b) Phần parabol (P) nằm phía trên trục hoành ứng với những giá trị nào của x.
Phương pháp giải:
- Nếu dấu bất phương trình dương thì bất phương trình biểu diễn phần (P) phía trên trục hoành và ngược lại.
Lời giải chi tiết:
a) Từ đồ thị ta thấy bất phương trình (2) biểu diễn phần parabol (P) nằm ở phía trên trục hoành.
b) Phần parabol (P) nằm phía trên trục hoành ứng với các giá trị của x thuộc \(\left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\)
a) Lập bảng xét dấu của tam thức bậc hai \(f\left( x \right) = {x^2} - x - 2\)
b) Giải bất phương trình \({x^2} - x - 2 > 0\)
Phương pháp giải:
a) Tìm nghiệm của phương trình \({x^2} - x - 2 = 0\), xét hệ số và lập bảng xét dấu.
b) Dựa vào bảng xét dấu, lấy các khoảng để \(f\left( x \right) > 0\)
Lời giải chi tiết:
a) Ta có tam thức bậc hai \(f\left( x \right) = {x^2} - x - 2\) có 2 nghiệm phân biệt \({x_1} = - 1,{x_2} = 2\) và hệ số \(a = 1 > 0\)
Ta có bảng xét dấu f(x) như sau:

Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)\)b) Từ bảng xét dấu ta thấy \(f\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}x < - 1\\x > 2\end{array} \right.\)
Giải các bất phương trình bậc hai sau:
a) \(3{x^2} - 2x + 4 \le 0\)
b) \( - {x^2} + 6x - 9 \ge 0\)
Phương pháp giải:
Giải bất phương trình dạng \(f\left( x \right) > 0\).
Bước 1: Xác định dấu của hệ số a và tìm nghiệm của \(f\left( x \right)\)(nếu có)
Bước 2: Sử dụng định lí về dấu của tam thức bậc hai để tìm tập hợp những giá trị của x sao cho \(f\left( x \right)\) mang dấu “+”
Bước 3: Các bất phương trình bậc hai có dạng \(f\left( x \right) < 0,f\left( x \right) \ge 0,f\left( x \right) \le 0\) được giải bằng cách tương tự.
Lời giải chi tiết:
a) Ta có \(a = 3 > 0\) và tam thức bậc hai \(f\left( x \right) = 3{x^2} - 2x + 4\) có \(\Delta ' = {1^2} - 3.4 = - 11 < 0\)
=> \(f\left( x \right) = 3{x^2} - 2x + 4\) vô nghiệm.
=> \(3{x^2} - 2x + 4 > 0\forall x \in \mathbb{R}\)
b) Ta có: \(a = - 1 < 0\) và \(\Delta ' = {3^2} - \left( { - 1} \right).\left( { - 9} \right) = 0\)
=> \(f\left( x \right) = - {x^2} + 6x - 9\) có nghiệm duy nhất \(x = 3\).
=> \( - {x^2} + 6x - 9 < 0\forall x \in \mathbb{R}\backslash \left\{ 3 \right\}\)
Cho bất phương trình \({x^2} - 4x + 3 > 0\left( 2 \right)\).
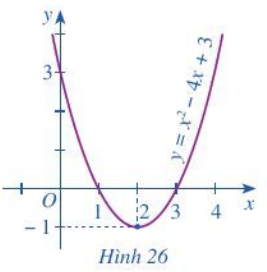
Quan sát parabol \(\left( P \right):{x^2} - 4x + 3\) ở Hình 26 và cho biết:
a) Bất phương trình (2) biểu diễn phần parabol (P) nằm ở phía nào của trục hoành.
b) Phần parabol (P) nằm phía trên trục hoành ứng với những giá trị nào của x.
Phương pháp giải:
- Nếu dấu bất phương trình dương thì bất phương trình biểu diễn phần (P) phía trên trục hoành và ngược lại.
Lời giải chi tiết:
a) Từ đồ thị ta thấy bất phương trình (2) biểu diễn phần parabol (P) nằm ở phía trên trục hoành.
b) Phần parabol (P) nằm phía trên trục hoành ứng với các giá trị của x thuộc \(\left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\)
Giải mỗi bất phương trình bậc hai sau bằng cách sử dụng đồ thị:
a) \({x^2} + 2x + 2 > 0\)
b) \( - 3{x^2} + 2x - 1 > 0\)
Phương pháp giải:
Bước 1: Vẽ đồ thị biểu diễn các hàm số.
Bước 2: Quan sát đồ thị và lấy các giá trị tương ứng với bất phương trình.
Lời giải chi tiết:
a) Ta có đồ thị:
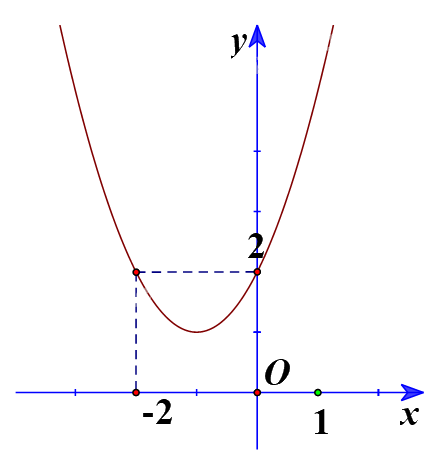
Từ đồ thị ta thấy \({x^2} + 2x + 2 > 0\) biểu diễn phần parabol \(y = {x^2} + 2x + 2\) nằm phía trên trục hoành, tương ứng với mọi \(x \in \mathbb{R}\).
Vậy tập nghiệm của bất phương trình \({x^2} + 2x + 2 > 0\) là \(\mathbb{R}\).
b) Ta có đồ thị:
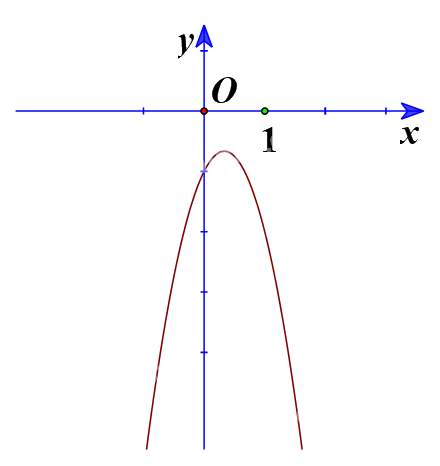
Từ đồ thị ta thấy \( - 3{x^2} + 2x - 1 > 0\) biểu diễn phần parabol \(y = - 3{x^2} + 2x - 1\) nằm phía trên trục hoành, tương ứng với \(x \in \emptyset \)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 2x - 1 > 0\) là \(\emptyset \).
Mục II trong SGK Toán 10 tập 1 - Cánh diều tập trung vào các khái niệm và bài tập liên quan đến vectơ. Cụ thể, trang 50 và 51 đề cập đến các nội dung như:
Đề bài: Cho tam giác ABC. Gọi M là trung điểm của BC. Tìm vectơ AM theo vectơ AB và AC.
Lời giải:
Áp dụng quy tắc trung điểm, ta có:
AM = (AB + AC) / 2
Vậy, vectơ AM được biểu diễn qua vectơ AB và AC là AM = (AB + AC) / 2.
Đề bài: Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh rằng OA = OC và OB = OD.
Lời giải:
Vì ABCD là hình bình hành nên:
Do đó, vectơ AB = vectơ DC và vectơ AD = vectơ BC.
Vì O là giao điểm của hai đường chéo AC và BD, ta có:
OA = OC (do AC là đường chéo của hình bình hành)
OB = OD (do BD là đường chéo của hình bình hành)
Vậy, OA = OC và OB = OD.
Đề bài: Cho ba điểm A, B, C không thẳng hàng. Xác định điểm D sao cho ABCD là hình bình hành.
Lời giải:
Để ABCD là hình bình hành, ta cần có:
AB song song và bằng CD, AD song song và bằng BC.
Từ đó, ta có thể suy ra:
vectơ AB = vectơ DC và vectơ AD = vectơ BC.
Dựa vào các điều kiện này, ta có thể xác định điểm D sao cho thỏa mãn.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, bạn đã có thể tự tin giải các bài tập trong mục II trang 50, 51 SGK Toán 10 tập 1 - Cánh diều. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!