Chào mừng các em học sinh đến với lời giải chi tiết bài 12 trang 104 SGK Toán 10 tập 2 – Cánh diều trên giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp các em tự tin hơn trong việc học tập môn Toán.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ các em học sinh nắm vững kiến thức và đạt kết quả tốt nhất.
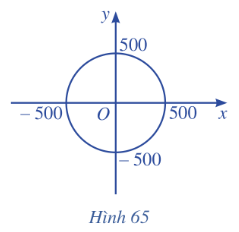
Trên màn hình ra đa của đài kiểm soát không lưu sân bay A có hệ trục toạ độ Oxy (Hình 65), trong đó đơn vị trên mỗi trục tính theo ki-lô-mét và đài kiểm soát được coi là gốc toạ độ O(0 : 0).
Đề bài
Trên màn hình ra đa của đài kiểm soát không lưu sân bay A có hệ trục toạ độ Oxy (Hình 65), trong đó đơn vị trên mỗi trục tính theo ki-lô-mét và đài kiểm soát được coi là gốc toạ độ O(0;0). Nếu máy bay bay trong phạm vi cách đài kiểm soát 500 km thì sẽ hiển thị trên màn hình ra đa như một điểm chuyển động trong mặt phẳng với hệ trục toạ độ Oxy. Một máy bay khởi hành từ sân bay B lúc 14 giờ. Sau thời gian t (giờ), vị trí của máy bay được xác định bởi điểm M có toạ độ như sau:\(\left\{ \begin{array}{l}x = \frac{{1600}}{3} - \frac{{1400}}{3}t\\y = \frac{{1900}}{3} - \frac{{1400}}{3}t\end{array} \right.\)
a) Tìm vị trí của máy bay lúc 14 giờ 30 phút. Thời điểm này máy bay đã xuất hiện trên màn hình ra đa chưa?
b) Lúc mấy giờ máy bay bay gần đài kiểm soát không lưu nhất? Tính khoảng cách giữa máy bay và đài kiểm soát không lưu lúc đó.
c) Máy bay ra khỏi màn hình ra đa vào thời gian nào?
Lời giải chi tiết
a) Máy bay khởi hành lúc 14h, đến 14h30 là đã di chuyển trong khoảng thời gian t = 30 phút bằng \(\frac{1}{2}\) giờ.
Thay \(t = \frac{1}{2}\) vào phương trình tọa độ điểm M, ta được vị trí máy bay vào lúc 14h30 là:
\(\left\{ \begin{array}{l}x = \frac{{1600}}{3} - \frac{{1400}}{3}.\frac{1}{2} = 300\\y = \frac{{1900}}{3} - \frac{{1400}}{3}.\frac{1}{2} = 400\end{array} \right.\)
Tọa độ máy bay là \(\left( {300;400} \right)\).
Khoảng cách từ đó đến đài kiểm soát là \(\sqrt {{{300}^2} + {{400}^2}} = 500\) km.
Thời điểm này máy bay đã xuất hiện trên màn hình ra đa.
b) Phương trình tọa độ điểm M đề bài cho cũng là phương trình đường bay d của máy bay.
Khoảng cách từ máy bay M đến đài kiểm soát O ngắn nhất khi M là hình chiếu của O trên d.
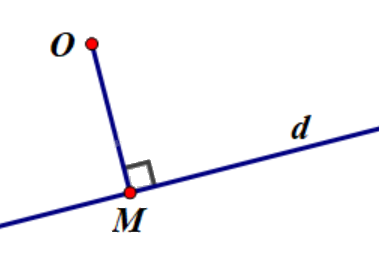
Khi đó \(\overrightarrow {{u_d}} .\overrightarrow {OM} = 0\) vì \(d \bot OM\).
Ta có \(\overrightarrow {OM} = \left( {\frac{{1600}}{3} - \frac{{1400}}{3}t;\frac{{1900}}{3} - \frac{{1400}}{3}t} \right)\);
\(\overrightarrow {{u_d}} = - \frac{3}{{1400}}.\left( { - \frac{{1400}}{3}t; - \frac{{1400}}{3}t} \right) = \left( {1;1} \right)\).
Suy ra \(\overrightarrow {OM} .\overrightarrow {{u_d}} = 0 \Leftrightarrow \frac{{1600}}{3} - \frac{{1400}}{3}t + \frac{{1900}}{3} - \frac{{1400}}{3}t = 0\)
\( \Leftrightarrow \frac{{3500}}{3} - \frac{{2800}}{3}t = 0 \Leftrightarrow t = \frac{5}{4}\).
Do đó \(M{O_{\min }} = 50\sqrt 2 \Leftrightarrow t = \frac{5}{4}\).
Vậy sau khi bay \(\frac{5}{4} = 1,25\) (giờ) tức là lúc 15h15p thì máy bay gần đài kiểm soát nhất và khoảng cách đó là \(50\sqrt 2 \) km.
c) Máy bay rời khỏi màn hình ra đa khi mà khoảng cách từ M đến O lớn hơn 500km tức là:
\(MO = \sqrt {{{\left( {\frac{{1600}}{3} - \frac{{1400}}{3}t} \right)}^2} + {{\left( {\frac{{1900}}{3} - \frac{{1400}}{3}t} \right)}^2}} > 500\)
\( \Leftrightarrow {\left( {\frac{{1600}}{3} - \frac{{1400}}{3}t} \right)^2} + {\left( {\frac{{1900}}{3} - \frac{{1400}}{3}t} \right)^2} > {500^2}\)
\( \Leftrightarrow {\left( {\frac{{1600}}{3}} \right)^2} - 2.\frac{{1600.1400}}{9}t + {\left( {\frac{{1400}}{3}} \right)^2}{t^2} + {\left( {\frac{{1900}}{3}} \right)^2} - 2.\frac{{1900.1400}}{9}t + {\left( {\frac{{1400}}{3}} \right)^2}{t^2} > {500^2}\)
\( \Leftrightarrow {\left( {\frac{{1600}}{3}} \right)^2} + {\left( {\frac{{1900}}{3}} \right)^2} - \frac{{2800}}{9}.(1600 + 1900)t + 2{\left( {\frac{{1400}}{3}} \right)^2}{t^2} > {500^2}\)
\( \Leftrightarrow \frac{{3920000}}{9} - \frac{{9800000}}{9}t + \frac{{3920000}}{9}{t^2} > 0\)
\( \Leftrightarrow 392 - 980t + 392{t^2} > 0\)
\( \Leftrightarrow x < \frac{1}{2}\) hoặc \(x > 2\).
Vậy máy bay bay ra khỏi màn hình ra đa vào khoảng thời gian từ 14 giờ đến trước 14 giờ 30 phút và sau 16 giờ.
Bài 12 trang 104 SGK Toán 10 tập 2 – Cánh diều thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về tích vô hướng của hai vectơ để giải quyết các bài toán liên quan đến góc giữa hai vectơ, độ dài vectơ và các ứng dụng thực tế.
Bài 12 bao gồm các câu hỏi và bài tập khác nhau, tập trung vào các nội dung sau:
Để giải bài 12 trang 104 SGK Toán 10 tập 2 – Cánh diều hiệu quả, các em cần nắm vững các kiến thức và công thức sau:
Dưới đây là lời giải chi tiết cho từng câu hỏi và bài tập trong bài 12 trang 104 SGK Toán 10 tập 2 – Cánh diều:
Cho hai vectơ a = (2, 3) và b = (-1, 4). Tính tích vô hướng của a và b.
Lời giải:
a.b = (2)(-1) + (3)(4) = -2 + 12 = 10
Cho hai vectơ u = (1, -1) và v = (0, 1). Tính góc giữa hai vectơ u và v.
Lời giải:
u.v = (1)(0) + (-1)(1) = -1
|u| = √(12 + (-1)2) = √2
|v| = √(02 + 12) = 1
cos(θ) = (u.v) / (|u||v|) = -1 / (√2 * 1) = -1/√2
θ = arccos(-1/√2) = 135°
Cho tam giác ABC có A(1, 2), B(3, 4), C(5, 1). Chứng minh rằng tam giác ABC vuông tại B.
Lời giải:
Tính vectơ BA và BC:
BA = (3-1, 4-2) = (2, 2)
BC = (5-3, 1-4) = (2, -3)
Tính tích vô hướng của BA và BC:
BA.BC = (2)(2) + (2)(-3) = 4 - 6 = -2
Vì BA.BC ≠ 0, nên tam giác ABC không vuông tại B.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập sau:
Bài 12 trang 104 SGK Toán 10 tập 2 – Cánh diều là một bài tập quan trọng giúp các em hiểu sâu hơn về tích vô hướng của hai vectơ và các ứng dụng của nó. Hy vọng rằng với lời giải chi tiết và phương pháp giải rõ ràng trên đây, các em sẽ tự tin hơn trong việc học tập môn Toán.