Chào mừng bạn đến với bài học về Lý thuyết Hoán vị và Chỉnh hợp trong chương trình Toán 10 Cánh diều. Đây là một trong những chủ đề quan trọng giúp bạn xây dựng nền tảng vững chắc cho các kiến thức toán học nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, bài giảng chi tiết và bài tập có đáp án để giúp bạn hiểu rõ và nắm vững kiến thức về Hoán vị và Chỉnh hợp.
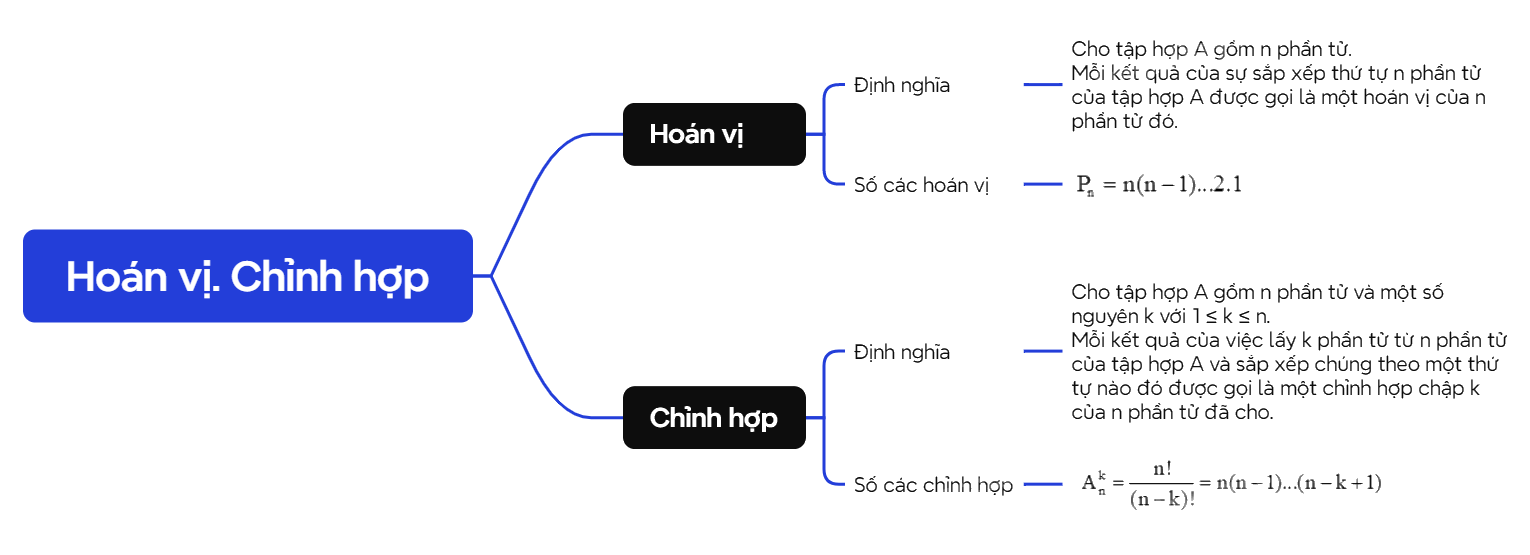
A. Lý thuyết 1. Hoán vị a) Định nghĩa
A. Lý thuyết
1. Hoán vị
a) Định nghĩa
Cho tập hợp A gồm n phần tử \(\left( {n \in {\mathbb{N}^*}} \right)\). Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó. |
b) Số các hoán vị
| Kí hiệu \({P_n}\) là số các hoán vị của n phần tử. Ta có \({P_n} = n(n - 1)...2.1\). |
2. Chỉnh hợp
a) Định nghĩa
Trong thực tiễn, bên cạnh việc chọn ra một số đối tượng từ những đối tượng cho trước, ta còn cần sắp xếp thứ tự của những đối tượng được chọn ra.
Cho tập hợp A gồm n phần tử và một số nguyên k với \(1 \le k \le n\). Mỗi kết quả của việc lấy k phần tử từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho. |
b) Số các chỉnh hợp
Kí hiệu \(A_n^k\) là số các chỉnh hợp chập k của n phần tử \((1 \le k \le n)\). Ta có: \(A_n^k = \frac{{n!}}{{(n - k)!}} = n(n - 1)...(n - k + 1)\). |
Nhận xét: \(A_n^n = {P_n}\) \(\forall n \in {\mathbb{N}^*}\).
B. Bài tập
Bài 1: Hãy liệt kê các số gồm ba chữ số đôi một khác nhau được lập từ các chữ số 1, 2, 3.
Giải:
Các số gồm ba chữ số đôi một khác nhau được lập từ các chữ số 1, 2, 3 là: 123, 132, 213, 231, 312, 321.
Bài 2: Tính số cách xếp thứ tự đã luân lưu 11 m của 5 cầu thủ.
Giải:
Mỗi cách xếp thứ tự đã luận lưu 11 m của 5 cầu thủ là một hoán vị của 5 cầu thủ.
Vậy số cách sắp xếp là: \({P_5} = 5.4.3.2.1 = 120\).
Bài 3: Hãy liệt kê các số gồm hai chữ số khác nhau được lấy từ các chữ số 1, 2, 3, 4, 5.
Giải:
Các số gồm hai chữ số khác nhau được lấy từ các chữ số 1, 2, 3, 4, 5 là: 12, 13, 14, 15, 21, 23, 24, 25, 31, 32, 34, 35, 41, 42, 43, 45, 51, 52, 53, 54.
Bài 4: Ở các căn hộ chung cư, người ta thường dùng các chữ số để tạo mật mã cửa. Gia đình bạn Linh đặt mật mã của là một dãy số gồm 6 chữ số đôi một khác nhau. Hỏi gia đình bạn Linh có bao nhiêu cách để tạo mật mã?
Giải:
Mỗi mật mã của gia đình bạn Linh là một chỉnh hợp chập 6 của 10 chữ số.
Vậy có \(A_{10}^6 = 10.9.8.7.6.5 = 151200\) (cách để tạo mật mã).
Hoán vị và Chỉnh hợp là hai khái niệm cơ bản trong tổ hợp, đóng vai trò quan trọng trong việc đếm số lượng các kết quả có thể xảy ra trong các tình huống thực tế. Bài viết này sẽ trình bày chi tiết lý thuyết về Hoán vị và Chỉnh hợp, cùng với các ví dụ minh họa và bài tập áp dụng theo SGK Toán 10 Cánh diều.
Trong nhiều bài toán, chúng ta cần xác định số lượng cách sắp xếp hoặc chọn ra một số đối tượng từ một tập hợp cho trước. Hoán vị và Chỉnh hợp là hai công cụ mạnh mẽ giúp chúng ta giải quyết những bài toán này.
Định nghĩa: Hoán vị của n phần tử là một cách sắp xếp n phần tử theo một thứ tự nhất định.
Công thức: Số hoán vị của n phần tử được ký hiệu là Pn và được tính bằng công thức:
Pn = n!
Trong đó, n! (n giai thừa) được tính bằng:
n! = n * (n-1) * (n-2) * ... * 2 * 1
Ví dụ: Có bao nhiêu cách sắp xếp 3 cuốn sách khác nhau trên một kệ sách?
Giải: Số cách sắp xếp là P3 = 3! = 3 * 2 * 1 = 6
Định nghĩa: Chỉnh hợp chập k của n phần tử là một cách sắp xếp k phần tử được chọn từ n phần tử theo một thứ tự nhất định.
Công thức: Số chỉnh hợp chập k của n phần tử được ký hiệu là Ank và được tính bằng công thức:
Ank = n! / (n-k)!
Ví dụ: Có bao nhiêu cách chọn và sắp xếp 2 học sinh từ một lớp 10 học sinh để làm nhiệm vụ?
Giải: Số cách chọn và sắp xếp là A102 = 10! / (10-2)! = 10! / 8! = 10 * 9 = 90
Bài 1: (SGK Toán 10 Cánh diều, trang...) Có bao nhiêu cách sắp xếp 5 bạn học sinh vào một hàng ngang?
Giải: Đây là một bài toán hoán vị. Số cách sắp xếp là P5 = 5! = 120
Bài 2: (SGK Toán 10 Cánh diều, trang...) Từ các chữ số 1, 2, 3, 4, 5, 6, có thể lập được bao nhiêu số có 4 chữ số khác nhau?
Giải: Đây là một bài toán chỉnh hợp. Số cách lập là A64 = 6! / (6-4)! = 6! / 2! = 360
Khi giải các bài toán về Hoán vị và Chỉnh hợp, cần xác định rõ:
Lý thuyết Hoán vị và Chỉnh hợp là nền tảng quan trọng cho việc giải quyết các bài toán đếm trong toán học. Việc nắm vững lý thuyết và luyện tập thường xuyên với các bài tập sẽ giúp bạn tự tin hơn trong các kỳ thi và ứng dụng kiến thức vào thực tế.