Chào mừng các em học sinh đến với lời giải chi tiết bài 8 trang 71 SGK Toán 10 tập 1 – Cánh diều. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu, nhanh chóng và chính xác.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em giải quyết mọi khó khăn trong môn Toán.
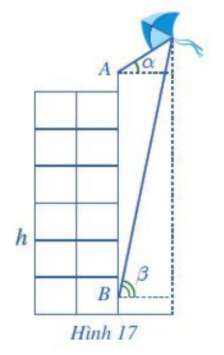
Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A tới chiếc diều và phương nằm ngang) là
Đề bài
Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A tới chiếc diều và phương nằm ngang) là \(\alpha = {35^o}\); khoảng cách từ đỉnh tòa nhà tới mắt bạn A là 1,5 m. Cùng lúc đó ở dưới chân tòa nhà, bạn B cũng quan sát chiếc diều và thấy góc nâng là \(\beta = {75^o}\); khoảng cách từ mặt đất đến mắt bạn B cũng là 1,5 m. Biết chiều cao của tòa nhà là h = 20 m (Hình 17). Chiếc diều bay cao bao nhiêu mét so mặt đất (làm tròn kết quả đến hàng đơn vị)?
Phương pháp giải - Xem chi tiết
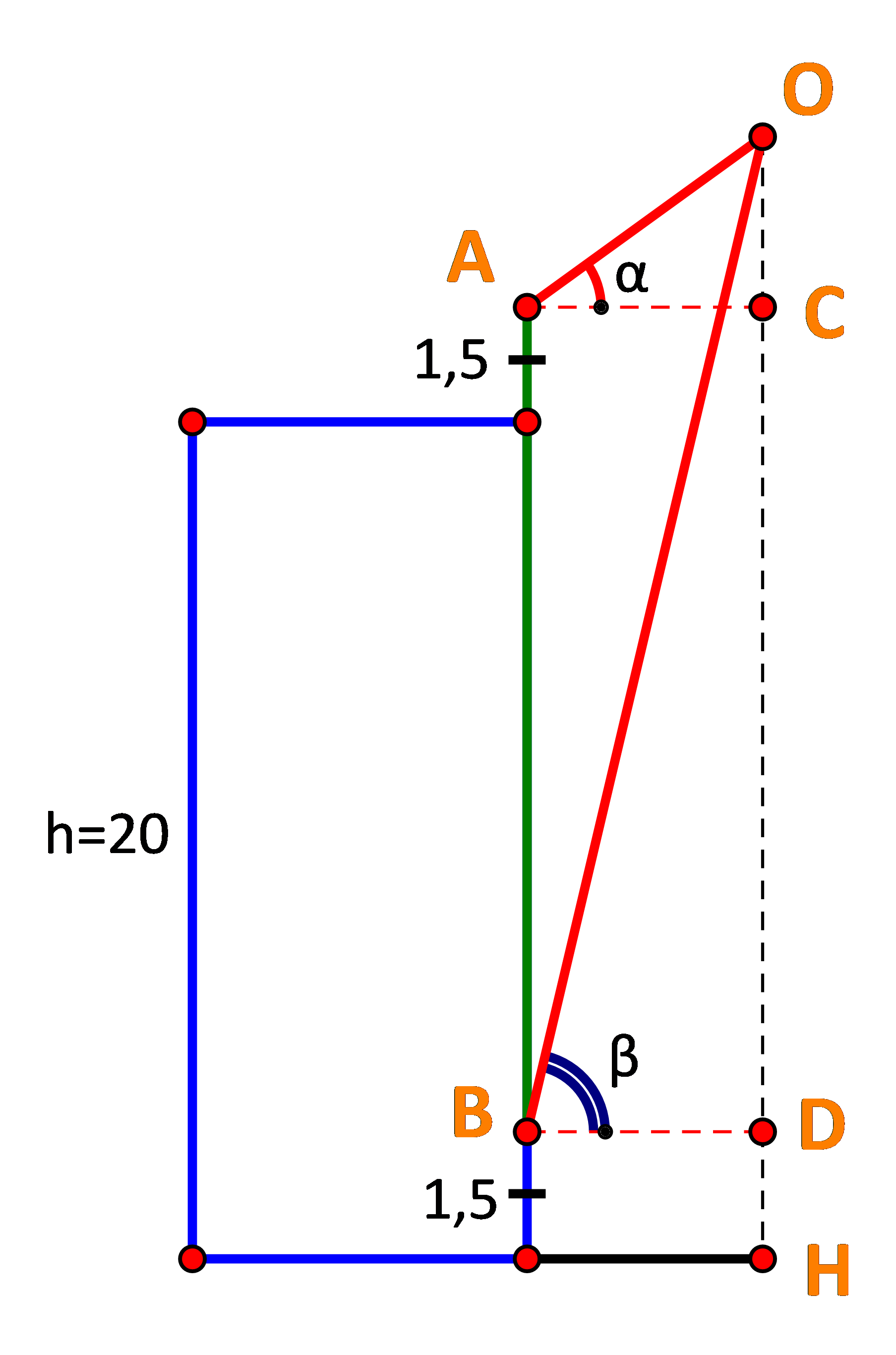
Bước 1: Vẽ hình, gọi các điểm O, C, D, H như hình vẽ.
Bước 2: Đặt x = OC. Tính AC, BD theo \(x,\alpha ,\beta \).
Bước 3: Lập luận tìm x. Từ đó suy ra khoảng cách OH.
Lời giải chi tiết
Gọi các điểm:
O là vị trí của chiếc diều.
H là hình chiếu vuông góc của chiếc diều trên mặt đất.
C, D lần lượt là hình chiếu vuông góc của A, B trên OH.
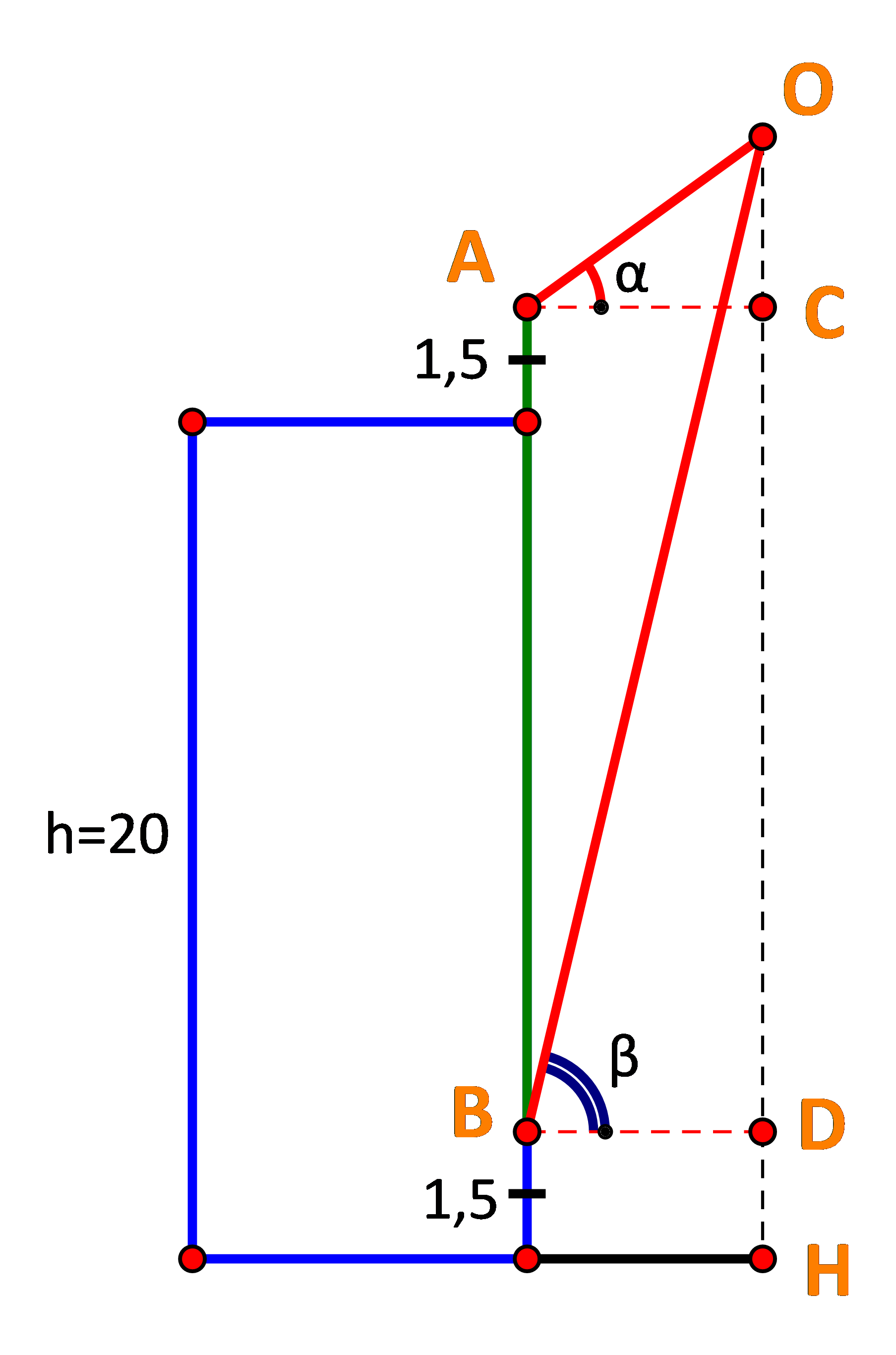
Đặt OC = x, suy ra OH = x + 20 + 1,5 = x + 21,5.
Xét tam giác OAC, ta có: \(\tan \alpha = \frac{{OC}}{{AC}} \Rightarrow AC = \frac{{OC}}{{\tan \alpha }} = \frac{x}{{\tan {{35}^o}}}\)
Xét tam giác OBD, ta có: \(\tan \beta = \frac{{OD}}{{BD}} \Rightarrow BD = \frac{{OD}}{{\tan \beta }} = \frac{{x + 20}}{{\tan {{75}^o}}}\)
Mà:\(AC = BD\)\( \Rightarrow \frac{x}{{\tan {{35}^o}}} = \frac{{x + 20}}{{\tan {{75}^o}}}\)
\(\begin{array}{l} \Leftrightarrow x.\tan {75^o} = \left( {x + 20} \right).\tan {35^o}\\ \Leftrightarrow x = \frac{{20.\tan {{35}^o}}}{{\tan {{75}^o} - \tan {{35}^o}}} \approx 4,6\end{array}\)
Suy ra OH = 26,1.
Vậy chiếc diều bay cao khoảng 26 m so với mặt đất.
Bài 8 trang 71 SGK Toán 10 tập 1 – Cánh diều thuộc chương trình học về Vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán vectơ, đặc biệt là phép cộng, trừ vectơ và phép nhân vectơ với một số thực để giải quyết các bài toán liên quan đến hình học.
Bài 8 bao gồm các câu hỏi và bài tập sau:
Để giải quyết bài 8 trang 71 SGK Toán 10 tập 1 – Cánh diều một cách hiệu quả, các em cần nắm vững các phương pháp sau:
(Nội dung câu 1 và lời giải chi tiết)
(Nội dung câu 2 và lời giải chi tiết)
(Nội dung câu 3 và lời giải chi tiết)
(Nội dung câu 4 và lời giải chi tiết)
Ví dụ: Cho tam giác ABC, với M là trung điểm của BC. Chứng minh rằng AB + AC = 2AM.
Lời giải:
Vì M là trung điểm của BC, ta có BM = MC. Do đó, BC = 2BM.
Áp dụng quy tắc hình bình hành, ta có:
AB + AC = AB + (AM + MC) = AB + AM + MC
Vì BM = MC, ta có AM = BM. Vậy:
AB + AC = AB + AM + BM = AB + (AM + BM) = AB + BC
Mà BC = 2BM, nên AB + AC = AB + 2BM. Tuy nhiên, cách tiếp cận này chưa đúng. Chúng ta cần sử dụng tính chất của trung điểm một cách trực tiếp hơn.
Ta có: AM = AB + BM và AM = AC + CM. Vì BM = CM, nên AB + AC = 2AM.
Để củng cố kiến thức về bài 8 trang 71 SGK Toán 10 tập 1 – Cánh diều, các em có thể tự giải thêm các bài tập tương tự trong sách bài tập hoặc trên các trang web học toán online.
Bài 8 trang 71 SGK Toán 10 tập 1 – Cánh diều là một bài tập quan trọng giúp các em hiểu sâu hơn về vectơ và các phép toán vectơ. Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà giaitoan.edu.vn cung cấp, các em sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.