Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 2 trang 48 SGK Toán 10 tập 1 – Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn tự tin chinh phục môn Toán.
Tìm nghiệm và lập bảng xét dấu của tam thức bậc hai f(x) với đồ thị được cho ở mỗi Hình 224a, 24b, 24c.
Đề bài
Tìm nghiệm và lập bảng xét dấu của tam thức bậc hai \(f\left( x \right)\) với đồ thị được cho ở mỗi Hình 224a, 24b, 24c.
Phương pháp giải - Xem chi tiết
- Quan sát đồ thị và hoành độ giao điểm của đồ thị với trục hoành là nghiệm của phương trình \(f\left( x \right) = 0\).
- Lập bảng xét dấu cho mỗi hình.
Lời giải chi tiết
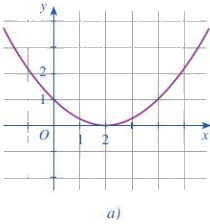
Hình 24a:
Ta thấy đồ thị cắt trục Ox tại điểm (2;0)
=> Phương trình \(f\left( x \right) = 0\) có nghiệm duy nhất \(x = 2\)
Ta thấy đồ thị nằm trên trục hoành nên có bảng xét dấu:

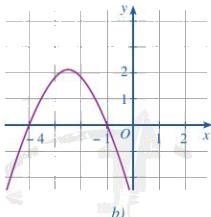
Hình 24b:
Ta thấy đồ thị cắt trục Ox tại 2 điểm phân biệt (-4;0) và (-1;0)
=> Phương trình \(f\left( x \right) = 0\) có 2 nghiệm phân biệt \(x = - 4,x = - 1\)
Trong các khoảng \(\left( { - \infty ; - 4} \right)\) và \(\left( { - 1; + \infty } \right)\) thì đồ thị nằm dưới trục hoành nên \(f\left( x \right) < 0\)
Trong khoảng \(\left( { - 4; - 1} \right)\) thì đồ thị nằm trên trục hoành nên \(f\left( x \right) > 0\)
Bảng xét dấu:
 Hình 24c:
Hình 24c:
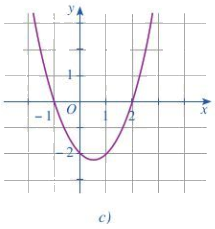
Ta thấy đồ thị cắt trục Ox tại 2 điểm phân biệt (-1;0) và (2;0)
=> Phương trình \(f\left( x \right) = 0\) có 2 nghiệm phân biệt \(x = - 1,x = 2\)
Trong các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {2; + \infty } \right)\) thì đồ thị nằm trên trục hoành nên \(f\left( x \right) > 0\)
Trong khoảng \(\left( { - 1;2} \right)\) thì đồ thị nằm dưới trục hoành nên \(f\left( x \right) < 0\)
Bảng xét dấu:

Bài 2 trang 48 SGK Toán 10 tập 1 – Cánh diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về tập hợp, các phép toán trên tập hợp, và các tính chất cơ bản của tập hợp để giải quyết các bài toán cụ thể. Bài tập này thường yêu cầu học sinh xác định các tập hợp, tìm phần tử thuộc tập hợp, thực hiện các phép hợp, giao, hiệu, bù của các tập hợp, và chứng minh các đẳng thức liên quan đến tập hợp.
Bài 2 trang 48 SGK Toán 10 tập 1 – Cánh diều thường bao gồm các câu hỏi và bài tập sau:
Để giải bài tập 2 trang 48 SGK Toán 10 tập 1 – Cánh diều một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Ví dụ: Cho A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Tìm A ∪ B và A ∩ B.
Giải:
Khi giải bài tập về tập hợp, bạn cần lưu ý những điều sau:
Để củng cố kiến thức và kỹ năng giải bài tập về tập hợp, bạn có thể thực hành thêm các bài tập sau:
Bài 2 trang 48 SGK Toán 10 tập 1 – Cánh diều là một bài tập quan trọng giúp bạn nắm vững kiến thức cơ bản về tập hợp. Bằng cách hiểu rõ định nghĩa, tính chất của tập hợp, sử dụng ký hiệu tập hợp, và áp dụng các phương pháp giải bài tập phù hợp, bạn có thể tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả. Chúc bạn học tập tốt!