Chào mừng bạn đến với bài học về Lý thuyết Giá trị lượng giác của một góc từ 0 đến 180, Định lí cosin và định lí sin trong tam giác - chương trình Toán 10 Cánh diều tại giaitoan.edu.vn. Bài viết này sẽ cung cấp kiến thức nền tảng, công thức quan trọng và các ví dụ minh họa giúp bạn nắm vững nội dung chương học.
Chúng tôi cam kết mang đến trải nghiệm học toán online hiệu quả, với nội dung được trình bày rõ ràng, dễ hiểu, phù hợp với mọi trình độ học sinh.
I. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0 ĐẾN 180 II. ĐỊNH LÍ COSIN III. ĐỊNH LÍ SIN
I. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0 ĐẾN 180
1. Giá trị lượng giác của một góc từ 0 đến 180
+) Với mỗi góc \(\alpha ({0^o} \le \alpha {\rm{\;}} \le {180^o})\) có duy nhất điểm \(M({x_0};{y_0})\) trên nửa đường tròn đơn vị để \(\widehat {xOM} = \alpha .\)Khi đó:
\(\sin \alpha {\rm{\;}} = {y_0}\) là tung độ của M
\(\cos \alpha {\rm{\;}} = {x_0}\) là hoành độ của M
\(\tan \alpha {\rm{\;}} = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha {\rm{\;}} \ne {90^o})\)
\(\cot \alpha {\rm{\;}} = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha {\rm{\;}} \ne {0^o},\alpha {\rm{\;}} \ne {180^o})\)
2. Quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Hai góc bù nhau, \(\alpha \) và \({180^o} - \alpha \): \(\begin{array}{*{20}{l}}{\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha }\\{\cos \left( {{{180}^o} - \alpha } \right) = {\rm{\;}} - \cos \alpha }\\{\tan \left( {{{180}^o} - \alpha } \right) = {\rm{\;}} - \tan \alpha (\alpha {\rm{\;}} \ne {{90}^o})}\\{\cot \left( {{{180}^o} - \alpha } \right) = {\rm{\;}} - \cot \alpha ({0^o} < \alpha {\rm{\;}} < {{180}^o})}\end{array}\) | Hai góc phụ nhau, \(\alpha \) và \({90^o} - \alpha \): \(\begin{array}{*{20}{l}}{\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha }\\{\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha }\\{\tan \left( {{{90}^o} - \alpha } \right) = \cot \alpha (\alpha {\rm{\;}} \ne {{90}^o},{0^o} < \alpha {\rm{\;}} < {{180}^o})}\\{\cot \left( {{{90}^o} - \alpha } \right) = \tan \alpha (\alpha {\rm{\;}} \ne {{90}^o},{0^o} < \alpha {\rm{\;}} < {{180}^o})}\end{array}\) |
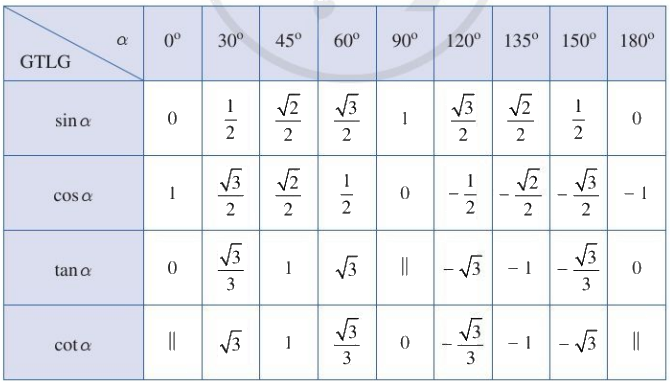
3. Các giá trị lượng giác của một số góc đặc biệt
II. ĐỊNH LÍ COSIN
1. Định lí cosin
Trong tam giác ABC:
\(\begin{array}{*{20}{l}}{{a^2} = {b^2} + {c^2} - 2bc\cos A}\\{{b^2} = {c^2} + {a^2} - 2ca\cos B}\\{{c^2} = {a^2} + {b^2} - 2ab\cos C}\end{array}\)
2. Hệ quả
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\)
III. ĐỊNH LÍ SIN
1. Định lí sin
Trong tam giác ABC: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.\)
(R là bán kính đường tròn ngoại tiếp tam giác ABC)
2. Hệ quả
Hệ quả
\(a = 2R.\sin A;\quad b = 2R\sin B;\quad c = 2R\sin C\)
\(\sin A = \frac{a}{{2R}};\quad \sin B = \frac{b}{{2R}};\quad \sin C = \frac{c}{{2R}}.\)
Trong chương trình Toán 10, phần Lý thuyết Giá trị lượng giác của một góc từ 0 đến 180° đóng vai trò quan trọng trong việc xây dựng nền tảng cho các kiến thức hình học và lượng giác nâng cao. Bài viết này sẽ trình bày chi tiết các khái niệm, định nghĩa và công thức liên quan đến chủ đề này, đồng thời cung cấp các ví dụ minh họa để giúp bạn hiểu rõ hơn.
Góc lượng giác là góc được tạo bởi tia gốc và tia cuối. Số đo của cung là số đo của góc lượng giác tương ứng. Có hai đơn vị đo góc phổ biến là độ (°) và radian (rad). Mối quan hệ giữa độ và radian là: 180° = π rad.
Đối với một góc α (0° ≤ α ≤ 180°), ta định nghĩa các giá trị lượng giác sau:
Các giá trị lượng giác này có thể được xác định thông qua đường tròn lượng giác.
Một số góc đặc biệt có giá trị lượng giác quen thuộc, cần được ghi nhớ:
| Góc α | sin α | cos α | tan α | cot α |
|---|---|---|---|---|
| 0° | 0 | 1 | 0 | Không xác định |
| 30° | 1/2 | √3/2 | 1/√3 | √3 |
| 45° | √2/2 | √2/2 | 1 | 1 |
| 60° | √3/2 | 1/2 | √3 | 1/√3 |
| 90° | 1 | 0 | Không xác định | 0 |
| 180° | 0 | -1 | 0 | Không xác định |
Định lý cosin là một công cụ mạnh mẽ để giải tam giác khi biết hai cạnh và góc xen giữa, hoặc ba cạnh. Phát biểu của định lý cosin như sau:
Trong tam giác ABC, ta có:
Trong đó: a, b, c là độ dài các cạnh của tam giác, A, B, C là các góc đối diện với các cạnh tương ứng.
Định lý sin là một công cụ quan trọng để giải tam giác khi biết một cạnh và hai góc, hoặc hai cạnh và góc đối diện với một trong hai cạnh đó. Phát biểu của định lý sin như sau:
Trong tam giác ABC, ta có:
a/sin A = b/sin B = c/sin C
Định lý cosin và định lý sin được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến tam giác, đặc biệt là trong các lĩnh vực như đo đạc, hàng hải, và kỹ thuật.
Để củng cố kiến thức, bạn có thể thực hành giải các bài tập sau:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Giá trị lượng giác của một góc từ 0 đến 180°, Định lý cosin và Định lý sin trong tam giác. Chúc bạn học tập tốt!