Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 77 SGK Toán 10 tập 1 – Cánh diều. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu, nhanh chóng và chính xác.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em giải quyết mọi khó khăn trong môn Toán.
Để tính khoảng cách giữa hai địa điểm A và B mà ta không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB.
Đề bài
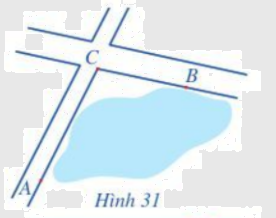
Để tính khoảng cách giữa hai địa điểm A và B mà ta không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB. Sau khi đo, ta nhận được: AC = 1 km, CB = 800 m và \(\widehat {ACB} = {105^o}\) (Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười đơn vị mét).
Phương pháp giải - Xem chi tiết
Bước 1: Đổi độ dài AC, CB về cùng đơn vị mét.
Bước 2: Tính AB: Áp dụng định lí cosin trong tam giác BAC: \(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)
Lời giải chi tiết
Đổi: 1 km = 1000 m. Do đó AC = 1000 m.
Áp dụng định lí cosin trong tam giác ABC ta có:
\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)
\(\begin{array}{l} \Rightarrow A{B^2} = {1000^2} + {800^2} - 2.1000.800.\cos {105^o}\\ \Rightarrow A{B^2} \approx 2054110,5\\ \Rightarrow AB \approx 1433,2\end{array}\)
Vậy khoảng cách AB là 1433,2 m.
Bài 6 trang 77 SGK Toán 10 tập 1 – Cánh diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của chúng.
Bài 6 trang 77 SGK Toán 10 tập 1 – Cánh diều thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài 6 trang 77 SGK Toán 10 tập 1 – Cánh diều. (Nội dung giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, giải thích rõ ràng, và sử dụng hình vẽ minh họa nếu cần thiết. Ví dụ:)
Đề bài: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng AB + AC = 2AM.
Lời giải:
Để củng cố kiến thức về vectơ và các phép toán vectơ, các em có thể tự giải thêm các bài tập tương tự trong SGK Toán 10 tập 1 – Cánh diều hoặc các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn khi giải các bài tập khó.
Bài 6 trang 77 SGK Toán 10 tập 1 – Cánh diều là một bài tập quan trọng giúp các em hiểu sâu hơn về vectơ và các ứng dụng của chúng trong hình học. Hy vọng rằng với lời giải chi tiết và các lưu ý trên, các em sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả.