Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 92 SGK Toán 10 tập 2 – Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập hiệu quả, giúp các em tự tin hơn trong quá trình học tập môn Toán.
Bài 6 thuộc chương trình học Toán 10 tập 2, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học.
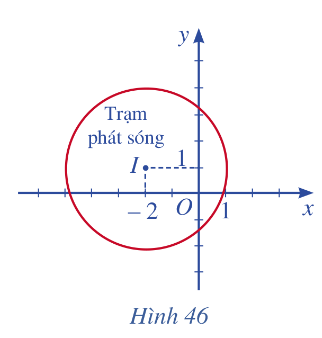
Hình 46 mô phỏng một trạm thu phát sóng điện thoại di động đặt ở vị trí 1 có toạ độ (- 2 ; 1) trong mặt phẳng toạ độ (đơn vị trên hai trục là ki-lô-mét).
Đề bài
Hình 46 mô phỏng một trạm thu phát sóng điện thoại di động đặt ở vị trí 1 có toạ độ (- 2 ; 1) trong mặt phẳng toạ độ (đơn vị trên hai trục là ki-lô-mét).
a) Lập phương trình đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng, biết rằng trạm thu phát sóng đó được thiết kế với bán kính phủ sóng 3 km.
b) Nếu người dùng điện thoại ở vị trí có toạ độ (-1;3) thì có thể sử dụng dịch vụ của trạm này không? Giải thích.
c) Tính theo đường chim bay, xác định khoảng cách ngắn nhất để một người ở vị trí có toạ độ (-3;4) di chuyển được tới vùng phủ sóng theo đơn vị ki-lô-mét (làm tròn kết quả đến hàng phần mười).
Phương pháp giải - Xem chi tiết
a) Đường tròn có tâm \(I\left( {a;b} \right)\) và bán kính R có phương trình là: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\)
Lời giải chi tiết
a) Phương trình đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng là: \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 9\)
b) Khoảng cách từ tâm I đến A là: \(IA = \sqrt {{{\left( { - 1 + 2} \right)}^2} + {{\left( {3 - 1} \right)}^2}} = \sqrt 5 \)
Do \(IA < 3\) nên điểm A nằm trong đường tròn ranh giới. Vậy nên người A có thể dịch vụ của trạm.
c) Khoảng cách từ tâm I đến B là: \(IB = \sqrt {{{\left( { - 3 + 2} \right)}^2} + {{\left( {4 - 1} \right)}^2}} = \sqrt {10} \)
Khoảng cách ngắn nhất theo đường chim bay để 1 người ở B di chuyển đến vùng phủ sóng là:
\(IB - R = \sqrt {10} - 3\left( {km} \right)\)
Bài 6 trang 92 SGK Toán 10 tập 2 – Cánh diều yêu cầu học sinh vận dụng kiến thức về vectơ, đặc biệt là các phép toán vectơ như cộng, trừ, nhân với một số thực, và tích vô hướng để giải quyết các bài toán liên quan đến hình học phẳng. Để giải quyết bài toán này một cách hiệu quả, trước hết chúng ta cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Để cung cấp lời giải chi tiết, chúng ta cần xem xét nội dung cụ thể của bài 6. Giả sử bài 6 yêu cầu chứng minh một đẳng thức vectơ hoặc giải một bài toán hình học sử dụng vectơ. Dưới đây là một ví dụ minh họa cách tiếp cận:
Giả sử bài toán yêu cầu chứng minh rằng với mọi điểm O, M, N, ta có: OM + MN = ON
Ngoài việc chứng minh đẳng thức vectơ, bài 6 trang 92 SGK Toán 10 tập 2 – Cánh diều có thể xuất hiện các dạng bài tập sau:
Để giải các bài tập này, các em cần:
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, các em có thể tham khảo các bài tập tương tự sau:
Các em có thể tìm thêm các bài tập tương tự trên giaitoan.edu.vn hoặc trong sách bài tập Toán 10 tập 2 – Cánh diều.
Bài 6 trang 92 SGK Toán 10 tập 2 – Cánh diều là một bài tập quan trọng giúp các em củng cố kiến thức về vectơ và ứng dụng vào giải quyết các bài toán hình học. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày ở trên, các em sẽ tự tin hơn trong quá trình học tập môn Toán.