Chào mừng các em học sinh đến với lời giải chi tiết bài 9 trang 61 SGK Toán 10 tập 1 – Cánh diều tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em hiểu rõ kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em chinh phục môn Toán một cách dễ dàng và thú vị.
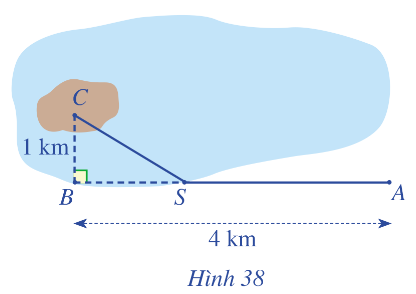
Một kĩ sư thiết kế đường dây điện từ vị trí A đến vị trí S và từ vị trí S đến vị trí C trên cù lao như Hình 38. Tiền công thiết kế mỗi ki-lô-mét đường dây từ A đến S và từ S đến C lần lượt là 3 triệu đồng và 5 triệu đồng. Biết tổng số tiền công là 16 triệu đồng. Tính tổng số ki-lô-mét đường dây điện đã thiết kế.
Đề bài
Một kĩ sư thiết kế đường dây điện từ vị trí A đến vị trí S và từ vị trí S đến vị trí C trên cù lao như Hình 38. Tiền công thiết kế mỗi ki-lô-mét đường dây từ A đến S và từ S đến C lần lượt là 3 triệu đồng và 5 triệu đồng. Biết tổng số tiền công là 16 triệu đồng. Tính tổng số ki-lô-mét đường dây điện đã thiết kế.
Lời giải chi tiết
Gọi khoảng cách từ A đến S là x (km) (0<x<4)
\( \Rightarrow BS = 4 - x\)(km)
\( \Rightarrow CS = \sqrt {C{B^2} + B{S^2}} \)\( = \sqrt {1 + \left( {4 - {x^2}} \right)} \)(km)
Tổng số tiền từ A đến C là:
\(3.SA + 5.SC = 3.x + 5.\sqrt {1 + {{\left( {4 - x} \right)}^2}} \)(triệu đồng)
Khi đó ta có phương trình:
\(3.x + 5.\sqrt {1 + {{\left( {4 - x} \right)}^2}} = 16\)
\( \Leftrightarrow 5\sqrt {1 + {{\left( {4 - x} \right)}^2}} = 16 - 3x\)
\(\begin{array}{l}25.\left( {{x^2} - 8x + 17} \right) = {\left( {16 - 3x} \right)^2}\\ \Leftrightarrow 25{x^2} - 200x + 425 = 256 - 96x + 9{x^2}\\ \Leftrightarrow 16{x^2} - 104x + 169 = 0\\ \Leftrightarrow x = \frac{{13}}{4}\left( {tm} \right)\end{array}\)
Do \(16 - 3x > 0 \Leftrightarrow \forall 0 < x < 4\)
=> \(SC = \sqrt {1 + \left( {4 - {x^2}} \right)} = 1,25\)
Vậy tổng ki-lô-mét đường dây điện đã thiết kế là SA+SC=3,25+1,25=4,5 (km)
Bài 9 trang 61 SGK Toán 10 tập 1 – Cánh diều thuộc chương 1: Mệnh đề và tập hợp. Bài tập này tập trung vào việc vận dụng các kiến thức về tập hợp, các phép toán trên tập hợp (hợp, giao, hiệu, phần bù) và các tính chất của chúng để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong môn Toán.
Bài 9 trang 61 SGK Toán 10 tập 1 – Cánh diều thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài 9 trang 61 SGK Toán 10 tập 1 – Cánh diều. (Ở đây sẽ là lời giải chi tiết cho từng câu hỏi của bài 9, ví dụ:)
Cho A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Tìm A ∪ B và A ∩ B.
Lời giải:
Cho A = {1, 2, 3} và B = {2, 4, 6}. Chứng minh A ∪ B = B ∪ A.
Lời giải:
Ta có: A ∪ B = {1, 2, 3, 4, 6} và B ∪ A = {2, 4, 6, 1, 3} = {1, 2, 3, 4, 6}. Do đó, A ∪ B = B ∪ A.
Ngoài bài 9 trang 61 SGK Toán 10 tập 1 – Cánh diều, các em có thể gặp các bài tập tương tự như sau:
Để giải quyết các bài tập này, các em cần:
Để học tốt môn Toán, đặc biệt là phần tập hợp, các em có thể áp dụng một số mẹo sau:
Hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, các em đã hiểu rõ hơn về cách giải bài 9 trang 61 SGK Toán 10 tập 1 – Cánh diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!