Lý thuyết Tổ hợp - SGK Toán 10 Cánh diều

Lý thuyết Tổ hợp - Nền tảng Toán học quan trọng

Chào mừng bạn đến với chuyên mục Lý thuyết Tổ hợp - SGK Toán 10 Cánh diều tại giaitoan.edu.vn. Đây là một trong những chủ đề quan trọng của chương trình Toán 10, đặt nền móng cho các kiến thức nâng cao hơn trong tương lai.

Chúng tôi cung cấp đầy đủ lý thuyết, ví dụ minh họa và bài tập thực hành để giúp bạn hiểu rõ và nắm vững kiến thức về tổ hợp, hoán vị, chỉnh hợp.

A. Lý thuyết 1. Định nghĩa

A. Lý thuyết

1. Định nghĩa

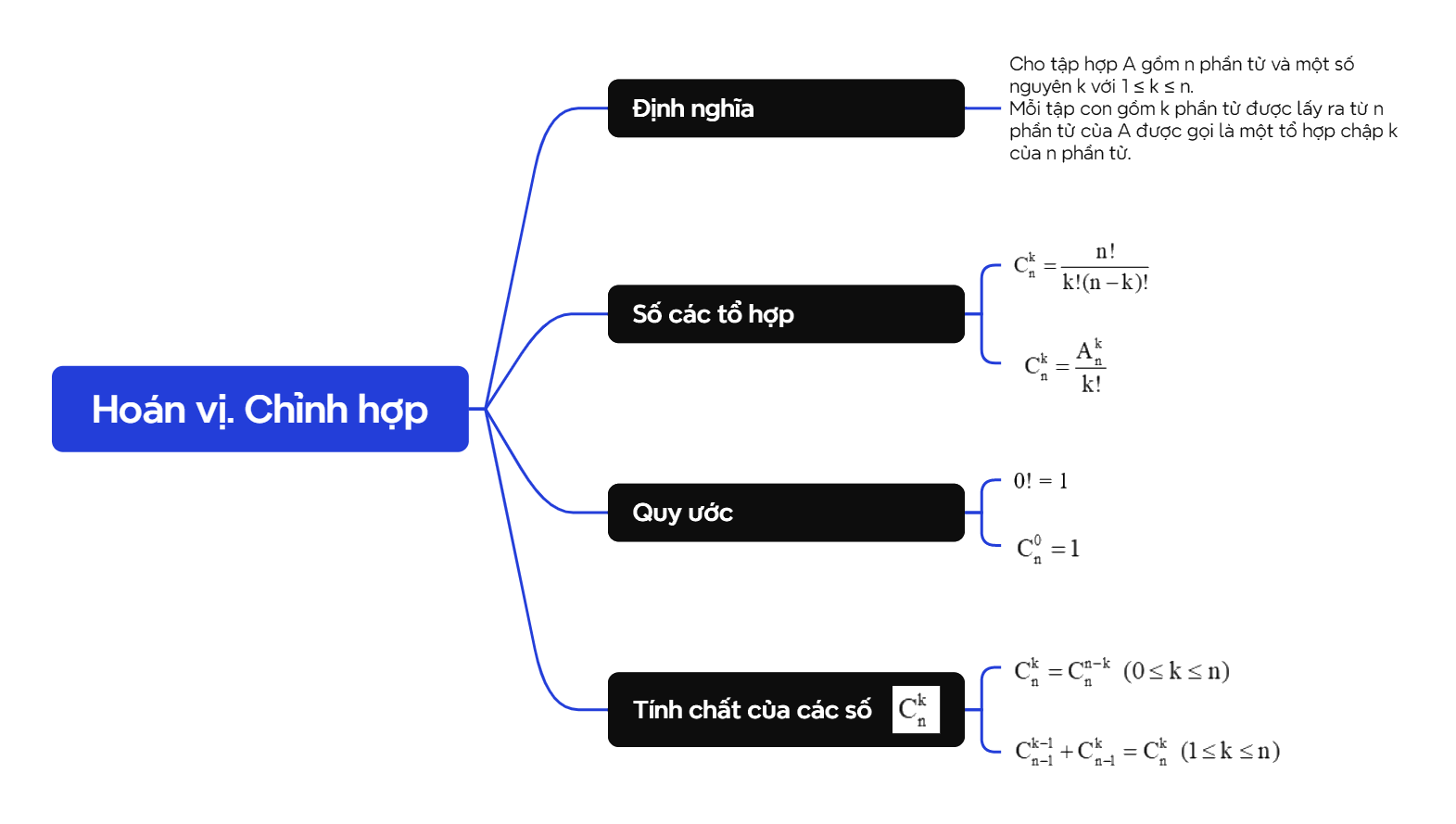
Cho tập hợp A gồm n phần tử và một số nguyên k với \(1 \le k \le n\).

Mỗi tập con gồm k phần tử được lấy ra từ n phần tử của A được gọi là một tổ hợp chập k của n phần tử.

2. Số các tổ hợp

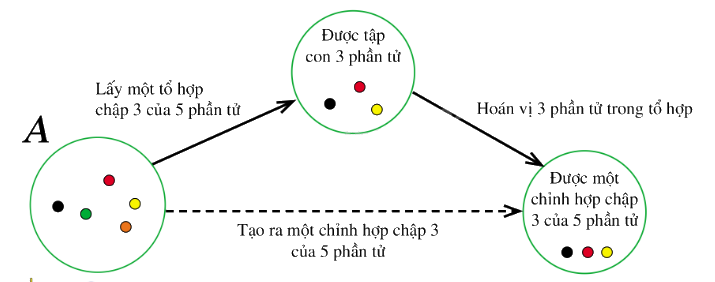
Lý thuyết Tổ hợp - SGK Toán 10 Cánh diều 1

Nhận xét: Số chỉnh hợp chập k của n phần tử nhiều gấp k! lần số tổ hợp chập k của n.

Kí hiệu \(C_n^k\) là số tổ hợp chập k của n phần tử với \(1 \le k \le n\). Ta có \(C_n^k = \frac{{A_n^k}}{{k!}}\).

Ngoài ra, ta có công thức \(C_n^k = \frac{{n!}}{{k!(n - k)!}}\) với

\(0 \le k \le n\).

Quy ước: 0! = 1; \(C_n^0 = 1\).

3. Tính chất của các số \(C_n^k\)

\(C_n^k = C_n^{n - k}\) \((0 \le k \le n)\) và \(C_{n - 1}^{k - 1} + C_{n - 1}^k = C_n^k\) \((1 \le k \le n)\)

B. Bài tập

Bài 1: Bạn Quân có 4 chiếc áo sơ mi khác màu là áo vàng, áo xanh, áo trắng và áo nâu. Bạn muốn chọn 2 chiếc áo để mặc khi đi du lịch. Viết các tổ hợp chập 2 của 4 chiếc áo.

Giải:

Các tổ hợp chập 2 của 4 chiếc áo là:

{áo vàng; áo xanh}, {áo vàng; áo trắng}, {áo vàng; áo nâu}, {áo xanh; áo trắng}, {áo xanh; áo nâu}, {áo trắng; áo nâu}.

Bài 2: Lớp 10A có 18 bạn nữ và 20 bạn nam.

a) Có bao nhiêu cách chọn 3 bạn nữ trong 18 bạn nữ?

b) Có bao nhiêu cách chọn 5 bạn nam trong 20 bạn nam?

c) Có bao nhiêu cách chọn một tổ xung kích gồm 3 bạn nữ và 5 bạn nam?

Giải:

a) Mỗi cách chọn 3 bạn nữ trong 18 bạn nữ là một tổ hợp chập 3 của 18 phần tử, do đó có \(C_{18}^3\) cách chọn.

b) Mỗi cách chọn 5 bạn nam trong 20 bạn nam là một tổ hợp chập 5 của 20 phần tử, do đó có \(C_{20}^5\) cách chọn.

c) Số cách chọn một tổ xung kích gồm 3 bạn nữ và 5 bạn nam là: \(C_{18}^3.C_{20}^5 = 816.15504 = 12651264\).

Lý thuyết Tổ hợp - SGK Toán 10 Cánh diều 2

Xây dựng nền tảng Toán THPT vững vàng từ hôm nay! Đừng bỏ lỡ Lý thuyết Tổ hợp - SGK Toán 10 Cánh diều đặc sắc thuộc chuyên mục bài tập toán 10 trên nền tảng đề thi toán. Với bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chương trình Toán lớp 10, đây chính là "kim chỉ nam" giúp các em tối ưu hóa ôn luyện, củng cố kiến thức cốt lõi và chuẩn bị hành trang vững chắc cho tương lai. Phương pháp học trực quan, logic sẽ mang lại hiệu quả vượt trội trên lộ trình chinh phục đại học!

Lý thuyết Tổ hợp - SGK Toán 10 Cánh diều: Tổng quan

Lý thuyết Tổ hợp là một nhánh quan trọng của Toán học, nghiên cứu về các cấu trúc rời rạc và các bài toán đếm. Trong chương trình Toán 10 Cánh diều, học sinh sẽ được làm quen với các khái niệm cơ bản như:

Quy tắc cộng: Nếu một công việc có thể được thực hiện theo một trong n cách khác nhau, không trùng lặp, thì số cách thực hiện công việc đó là n.
Quy tắc nhân: Nếu một công việc được thực hiện qua m giai đoạn, trong đó giai đoạn thứ i có n_i cách thực hiện, thì số cách thực hiện công việc đó là n₁ * n₂ * ... * n_m.
Hoán vị: Là một cách sắp xếp các phần tử của một tập hợp theo một thứ tự nhất định. Số hoán vị của n phần tử là n! (n giai thừa).
Chỉnh hợp: Là một cách chọn và sắp xếp k phần tử từ một tập hợp gồm n phần tử. Số chỉnh hợp chập k của n phần tử là A_n^k = n! / (n-k)!.
Tổ hợp: Là một cách chọn k phần tử từ một tập hợp gồm n phần tử, không quan tâm đến thứ tự. Số tổ hợp chập k của n phần tử là C_n^k = n! / (k! * (n-k)!).

Ứng dụng của Lý thuyết Tổ hợp

Lý thuyết Tổ hợp có rất nhiều ứng dụng trong thực tế, bao gồm:

Khoa học máy tính: Trong việc thiết kế thuật toán, phân tích độ phức tạp của thuật toán.
Thống kê: Trong việc tính toán xác suất, phân tích dữ liệu.
Kỹ thuật: Trong việc thiết kế hệ thống, tối ưu hóa quy trình.
Đời sống: Trong việc sắp xếp lịch trình, lựa chọn phương án.

Các dạng bài tập thường gặp

Trong SGK Toán 10 Cánh diều, các bài tập về Lý thuyết Tổ hợp thường tập trung vào các dạng sau:

Tính số phần tử của một tập hợp: Sử dụng quy tắc cộng, quy tắc nhân để tính số phần tử của một tập hợp.
Tính số hoán vị, chỉnh hợp, tổ hợp: Áp dụng công thức để tính số hoán vị, chỉnh hợp, tổ hợp trong các trường hợp cụ thể.
Giải các bài toán đếm: Sử dụng các kiến thức về tổ hợp để giải các bài toán đếm trong thực tế.
Bài toán về xác suất: Sử dụng tổ hợp để tính xác suất của các sự kiện.

Ví dụ minh họa

Ví dụ 1: Có bao nhiêu cách sắp xếp 5 cuốn sách khác nhau lên một kệ sách?

Giải: Đây là một bài toán về hoán vị. Số cách sắp xếp 5 cuốn sách là 5! = 5 * 4 * 3 * 2 * 1 = 120 cách.

Ví dụ 2: Từ một tập hợp gồm 7 người, chọn ra 3 người để thành lập một tổ xung kích. Hỏi có bao nhiêu cách chọn?

Giải: Đây là một bài toán về tổ hợp. Số cách chọn 3 người từ 7 người là C₇³ = 7! / (3! * 4!) = (7 * 6 * 5) / (3 * 2 * 1) = 35 cách.

Lời khuyên khi học Lý thuyết Tổ hợp

Nắm vững các định nghĩa và công thức: Đây là nền tảng để giải các bài tập.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.
Hiểu rõ bản chất của bài toán: Đọc kỹ đề bài, xác định đúng các yếu tố cần tìm và lựa chọn phương pháp giải phù hợp.
Sử dụng sơ đồ Venn: Sơ đồ Venn có thể giúp bạn hình dung rõ hơn về các tập hợp và mối quan hệ giữa chúng.