Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 4 trang 29 SGK Toán 10 tập 1 – Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn tự tin chinh phục môn Toán.
Một phân xưởng sản xuất hai kiểu mũ. Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai. Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc.
Đề bài
Một phân xưởng sản xuất hai kiểu mũ. Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai. Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc. Phân xưởng làm việc 8 tiếng mỗi ngày và thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai. Tiền lãi khi bán một chiếc mũ kiểu thứ nhất là 24 nghìn đồng, một chiếc mũ kiểu thứ hai là 15 nghìn đồng. Tính số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất để tiền lãi thu được là cao nhất.
Phương pháp giải - Xem chi tiết
Bước 1: Gọi số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất lần lượt là \(x\) và \(y\) \(\left( {x,y \in \mathbb{N}*} \right)\). Biểu diễn các đại lượng khác theo \(x\) và \(y\).
Bước 2: Lập hệ bất phương trình.
Bước 3: Biểu diễn miền nghiệm.
Bước 4: Tìm \(x\) và \(y\) để tiền lãi cao nhất.
Lời giải chi tiết
Bước 1: Gọi số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất lần lượt là \(x\) và \(y\) \(\left( {x,y \in \mathbb{N}} \right)\).
+ Theo giả thiết, thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất nên \(0 \le x \le 200\)
và 240 chiếc mũ kiểu thứ hai nên ta có \(0 \le y \le 240\)
+ Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc
=> Thời gian làm \(1\) chiếc mũ kiểu thứ hai là 1/60 (giờ)
=> Thời gian làm \(y\) chiếc kiểu hai là \(\frac{y}{{60}}\left( h \right)\)
+ Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai
=> thời gian làm 1 chiếc mũ kiểu thứ nhất là 2.1/60 = 1/30 (giờ)
=> Thời gian làm \(x\) chiếc kiểu thứ nhất là \(\frac{x}{{30}}\left( h \right)\)
+ Tổng thời gian làm một ngày không quá 8h nên ta có:
\(\frac{x}{{30}} + \frac{y}{{60}} \le 8\)
Bước 2: Lập hệ bất phương trình.
\(\left\{ \begin{array}{l}0 \le x \le 200\\0 \le y \le 240\\\frac{x}{{30}} + \frac{y}{{60}} \le 8\end{array} \right.\)
Bước 3: Biểu diễn miền nghiệm.
Miền biểu diễn miền nghiệm là phần không bị gạch, đa giác OABCD với O(0;0), A(0; 240), B(120; 240), C(200; 80), D(200; 0).
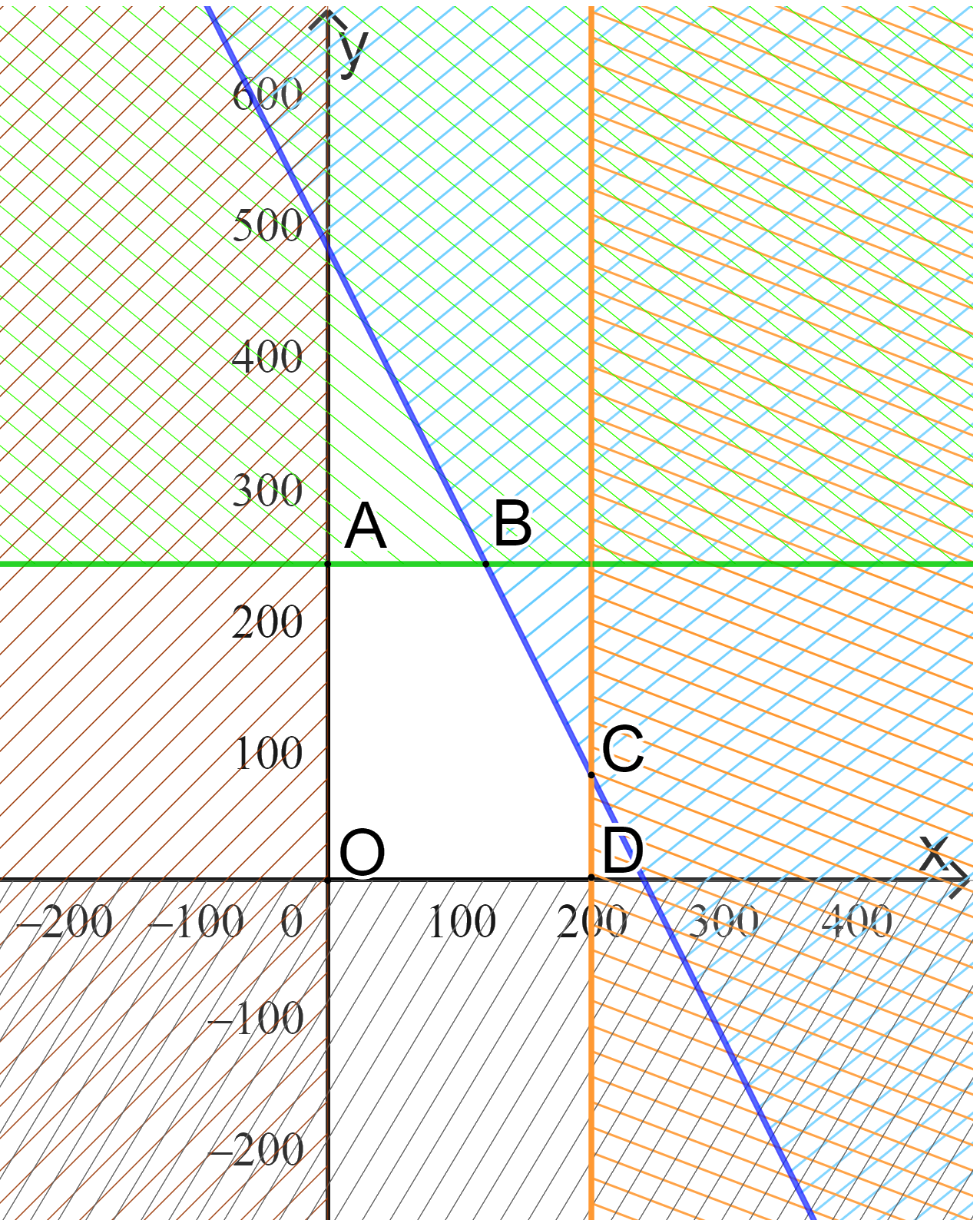
Bước 4: Tìm \(x\) và \(y\) để tiền lãi cao nhất.
Từ miền nghiệm ta thấy tiền lãi cao nhất tại khi điểm \(\left( {x;y} \right)\) là một trong các đỉnh của đa giác OABCD.
\(T = 24x + 15y\)
\(T\left( {0;240} \right) = 15.240 = 3600\) (nghìn đồng)
\(T\left( {120;240} \right) = 24.120+15.240 = 6480\) (nghìn đồng)
\(T\left( {200;80} \right) = 24.200+15.80 = 6000\) (nghìn đồng)
\(T\left( {200;0} \right) = 24.200 = 4800\)(nghìn đồng)
Vậy để tiền lãi thu được nhiều nhất, mỗi ngày xưởng cần sản xuất số mũ kiểu 1 là 120 và mũ kiểu 2 là 240 cái.
Bài 4 trang 29 SGK Toán 10 tập 1 – Cánh diều thuộc chương 1: Mệnh đề và tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về tập hợp, các phép toán trên tập hợp (hợp, giao, hiệu, phần bù) để giải quyết các bài toán cụ thể. Việc nắm vững các khái niệm và quy tắc này là nền tảng quan trọng cho việc học tập các kiến thức Toán học ở các lớp trên.
Bài 4 trang 29 SGK Toán 10 tập 1 – Cánh diều thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài 4 trang 29 SGK Toán 10 tập 1 – Cánh diều. (Ở đây sẽ là lời giải chi tiết cho từng câu hỏi của bài 4, ví dụ:)
Cho A = {1, 2, 3} và B = {2, 4, 5}. Tìm A ∪ B.
Lời giải:
A ∪ B = {1, 2, 3, 4, 5}.
Cho A = {1, 2, 3} và B = {2, 4, 5}. Tìm A ∩ B.
Lời giải:
A ∩ B = {2}.
Để giải quyết các bài tập về tập hợp một cách hiệu quả, bạn cần lưu ý những điều sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về tập hợp, bạn có thể tham khảo các bài tập tương tự sau:
Bài 4 trang 29 SGK Toán 10 tập 1 – Cánh diều là một bài tập quan trọng giúp bạn làm quen với các khái niệm và phép toán cơ bản về tập hợp. Hy vọng với lời giải chi tiết và những lưu ý trên, bạn sẽ tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả. Chúc bạn học tốt!
| Tập hợp A | Tập hợp B | A ∪ B | A ∩ B |
|---|---|---|---|
| {1, 2, 3} | {2, 4, 5} | {1, 2, 3, 4, 5} | {2} |
| {a, b, c} | {b, d, e} | {a, b, c, d, e} | {b} |