Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục III trang 75 và 76 của sách giáo khoa Toán 10 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là
Đề bài
Luyện tập – vận dụng 2 trang 76 SGK Toán 10 tập 1 – Cánh Diều
Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là \({34^o}\), góc lệch giữa phương quan sát ngọn cây và phương nằm ngang là \({24^o}\). Biết chiều cao của chân giác kế là 1,5 m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Lời giải chi tiết
Gọi A là vị trí đứng của Nam, B là điểm cao nhất của cây, C là vị trí gốc cây.
Gọi H là hình chiếu của A trên BC. Ta có hình vẽ:
TH1: Cây cao hơn tòa nhà
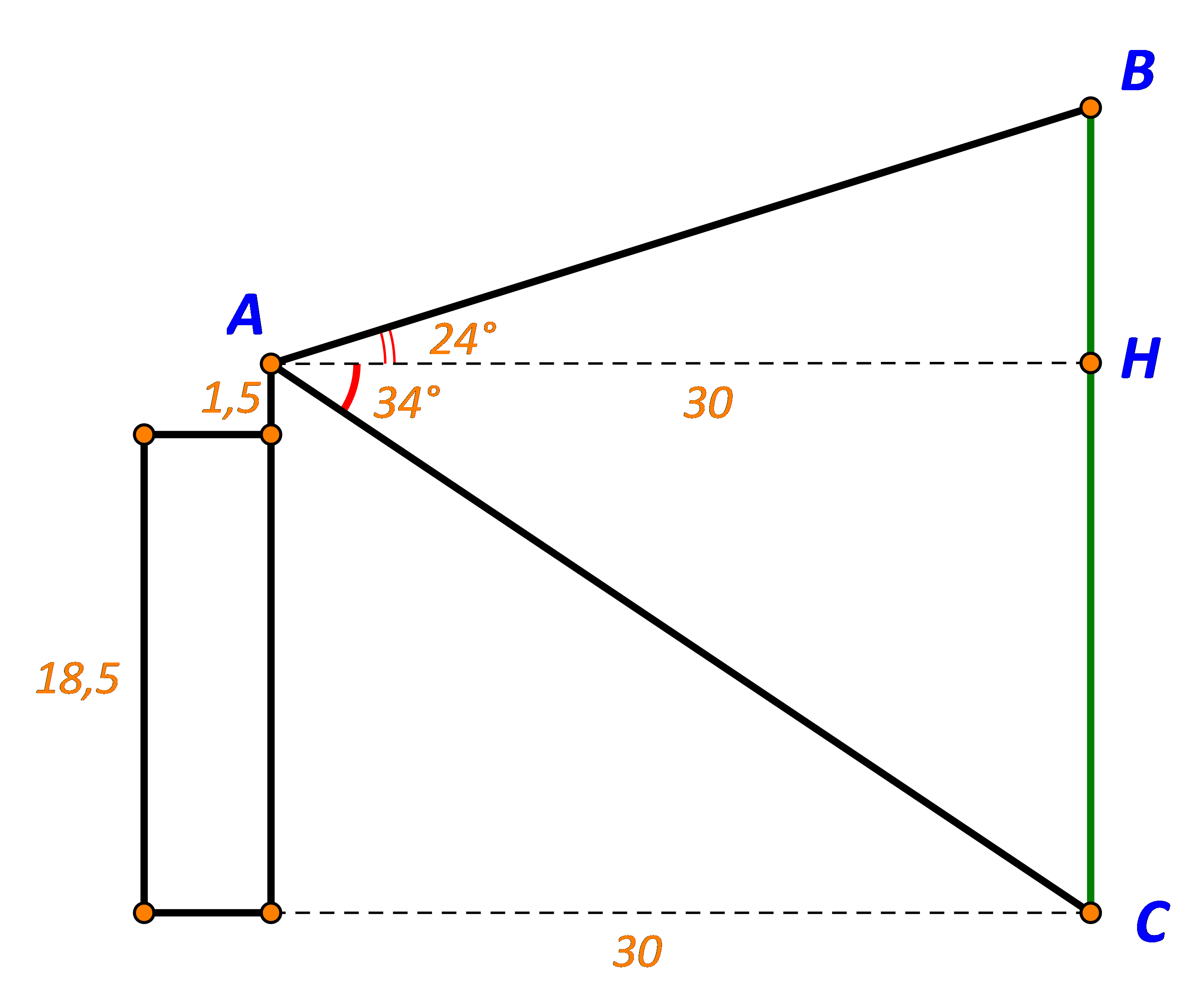
Ta có: \(\tan {24^ \circ } = \frac{{BH}}{{AH}} \Rightarrow BH = 30.\tan {24^ \circ } \approx 13,357\)
\( \Rightarrow BC = BH + HC \approx 13,357 + 1,5 + 18,5 = 33,357(m)\)
TH2: Cây thấp hơn tòa nhà
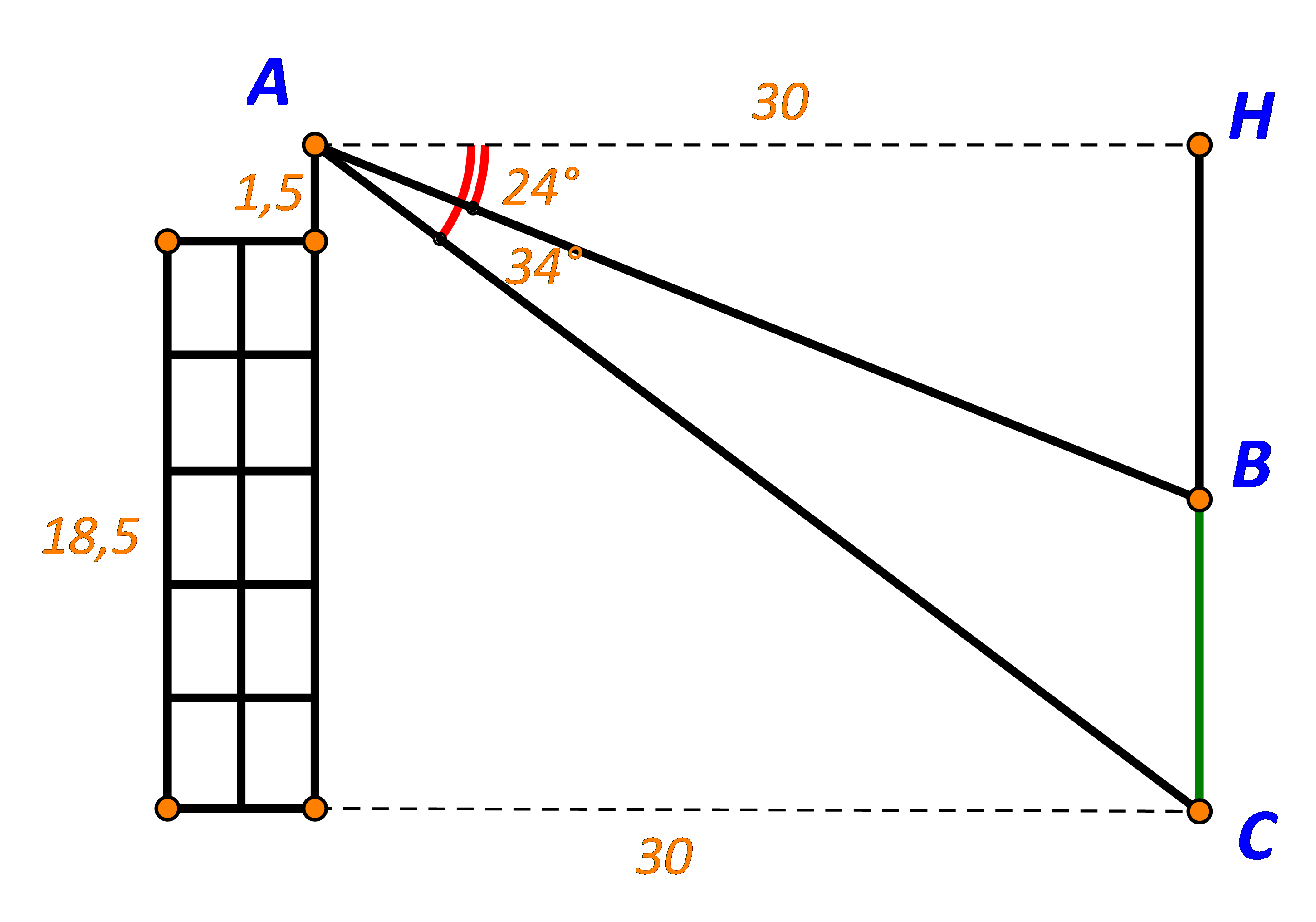
Ta có: \(\tan {24^ \circ } = \frac{{BH}}{{AH}} \Rightarrow BH = 30.\tan {24^ \circ } \approx 13,357\)
\( \Rightarrow BC = HC -HB \approx 1,5 + 18,5 - 13,357= 6,643(m)\)
Mục III trong SGK Toán 10 tập 1 - Cánh diều tập trung vào việc ứng dụng các kiến thức về vectơ trong hình học. Cụ thể, các bài tập trong mục này thường liên quan đến việc xác định tọa độ của vectơ, thực hiện các phép toán vectơ (cộng, trừ, nhân với một số thực) và sử dụng vectơ để chứng minh các tính chất hình học.
Bài tập 1 yêu cầu học sinh xác định tọa độ của các vectơ dựa trên tọa độ của các điểm trong mặt phẳng. Để giải bài tập này, học sinh cần nắm vững công thức tính tọa độ của vectơ khi biết tọa độ của điểm đầu và điểm cuối: AB = (xB - xA; yB - yA). Việc áp dụng chính xác công thức này là chìa khóa để giải quyết bài tập một cách nhanh chóng và chính xác.
Bài tập 2 tập trung vào việc thực hiện các phép toán cộng, trừ vectơ và nhân vectơ với một số thực. Để giải bài tập này, học sinh cần nhớ các quy tắc sau:
Bài tập 3 yêu cầu học sinh sử dụng kiến thức về vectơ để chứng minh các tính chất hình học, chẳng hạn như chứng minh hai đường thẳng song song, chứng minh ba điểm thẳng hàng, hoặc chứng minh một tứ giác là hình bình hành. Để giải bài tập này, học sinh cần kết hợp kiến thức về vectơ với các định lý và tính chất hình học đã học.
Cho A(1; 2), B(3; 4), C(-1; 0). Tìm tọa độ của vectơ AB, BC, CA.
Cho a = (1; -2), b = (3; 1). Tính a + b, a - b, 2a.
Chứng minh rằng tứ giác ABCD với A(1; 1), B(3; 2), C(4; 4), D(2; 3) là hình bình hành.
Để chứng minh ABCD là hình bình hành, ta cần chứng minh AB = DC và AD = BC.
| Vectơ | Tọa độ |
|---|---|
| AB | (3-1; 2-1) = (2; 1) |
| DC | (2-4; 3-4) = (-2; -1) |
| AD | (2-1; 3-1) = (1; 2) |
| BC | (4-3; 4-2) = (1; 2) |
Ta thấy AB = -DC và AD = BC. Do đó, tứ giác ABCD là hình bình hành.
Để học tốt môn Toán 10, bạn nên:
Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về cách giải các bài tập trong mục III trang 75, 76 SGK Toán 10 tập 1 - Cánh diều. Chúc bạn học tập tốt!