Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài tập 1.1 trang 13 SGK Toán 12 tập 1 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau: a) Đồ thị hàm số (y = {x^3} - frac{3}{2}{x^2}) (H.1.11); b) Đồ thị hàm số (y = sqrt[3]{{{{left( {{x^2} - 4} right)}^2}}}) (H.1.12).
Đề bài
Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:
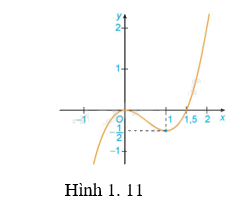
a) Đồ thị hàm số \(y = {x^3} - \frac{3}{2}{x^2}\) (H.1.11);
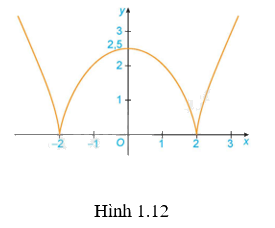
b) Đồ thị hàm số \(y = \sqrt[3]{{{{\left( {{x^2} - 4} \right)}^2}}}\) (H.1.12).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến của hàm số:
+ Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải.
+ Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải.
Lời giải chi tiết
a) Quan sát đồ thị trong hình thấy đồ thị đi lên từ trái sang trong các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {1; + \infty } \right)\).
Vậy hàm số \(y = {x^3} - \frac{3}{2}{x^2}\) đồng biến trên \(\left( { - \infty ;0} \right)\) và \(\left( {1; + \infty } \right)\).
Quan sát đồ thị trong hình thấy đồ thị đi xuống từ trái sang trong khoảng \(\left( {0;1} \right)\).
Hàm số \(y = {x^3} - \frac{3}{2}{x^2}\) nghịch biến trên \(\left( {0;1} \right)\).
b) Quan sát đồ thị trong hình thấy đồ thị đi lên từ trái sang trong các khoảng \(\left( { - 2;0} \right)\) và \(\left( {2; + \infty } \right)\).
Vậy hàm số \(y = \sqrt[3]{{{{\left( {{x^2} - 4} \right)}^2}}}\) đồng biến trên \(\left( { - 2;0} \right)\) và \(\left( {2; + \infty } \right)\).
Quan sát đồ thị trong hình thấy đồ thị đi xuống từ trái sang trong các khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {0;2} \right)\).
Hàm số \(y = \sqrt[3]{{{{\left( {{x^2} - 4} \right)}^2}}}\) nghịch biến trên \(\left( { - \infty ; - 2} \right)\) và \(\left( {0;2} \right)\).
Bài tập 1.1 trang 13 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương 1: Hàm số và đồ thị. Bài tập này tập trung vào việc ôn lại kiến thức về tập hợp số, các phép toán trên tập hợp và cách biểu diễn tập hợp. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các kiến thức tiếp theo về hàm số.
Bài tập 1.1 bao gồm các câu hỏi trắc nghiệm và bài tập tự luận. Các câu hỏi trắc nghiệm thường yêu cầu học sinh lựa chọn đáp án đúng trong các phương án cho trước. Các bài tập tự luận yêu cầu học sinh trình bày lời giải chi tiết và rõ ràng.
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài tập 1.1:
Nội dung câu hỏi...
Lời giải:
Nội dung câu hỏi...
Lời giải:
Nội dung câu hỏi...
Lời giải:
...
Để hiểu sâu hơn về các khái niệm liên quan đến bài tập 1.1, bạn có thể tham khảo thêm các tài liệu sau:
Khi giải bài tập 1.1, bạn cần lưu ý những điều sau:
Kiến thức về tập hợp số và các phép toán trên tập hợp có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học, đặc biệt là trong việc học hàm số, phương trình, bất phương trình và các bài toán thực tế.
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự sau:
Hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, bạn đã có thể giải bài tập 1.1 trang 13 SGK Toán 12 tập 1 - Kết nối tri thức một cách dễ dàng và hiệu quả. Chúc bạn học tốt!
| Khái niệm | Giải thích |
|---|---|
| Tập hợp số | Là một tập hợp chứa các số. |
| Phép hợp | Là phép toán kết hợp các phần tử của hai tập hợp. |
| Phép giao | Là phép toán chỉ lấy các phần tử chung của hai tập hợp. |
| Bảng tóm tắt các khái niệm quan trọng. | |