Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 1.23 trang 32 SGK Toán 12 tập 1 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải cụ thể, giúp bạn hiểu rõ bản chất của bài toán.
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: a) \(y = \frac{{2{x^2} - x + 4}}{{x - 1}}\); b) \(y = \frac{{{x^2} + 2x + 1}}{{x + 3}}\).
Đề bài
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:a) \(y = \frac{{2{x^2} - x + 4}}{{x - 1}}\);b) \(y = \frac{{{x^2} + 2x + 1}}{{x + 3}}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về sơ đồ khảo sát hàm số phân thức để khảo sát và vẽ đồ thị hàm số:
Sơ đồ khảo sát hàm số phân thức
1. Tìm tập xác định của hàm số.
2. Khảo sát sự biến thiên của hàm số:
+ Tính đạo hàm y’. Tìm các điểm tại đó y’ bằng 0 hoặc đạo hàm không tồn tại.
+ Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số.
+ Tìm cực trị của hàm số.
+ Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số.
+ Lập bảng biến thiên của hàm số.
3. Vẽ đồ thị của hàm số dựa vào bảng biến thiên.
Lời giải chi tiết
a) 1. Tập xác định của hàm số: \(\mathbb{R}\backslash \left\{ 1 \right\}\)
2. Sự biến thiên:
Ta có: \(y = \frac{{2{x^2} - x + 4}}{{x - 1}} = 2x + 1 + \frac{5}{{x - 1}}\)
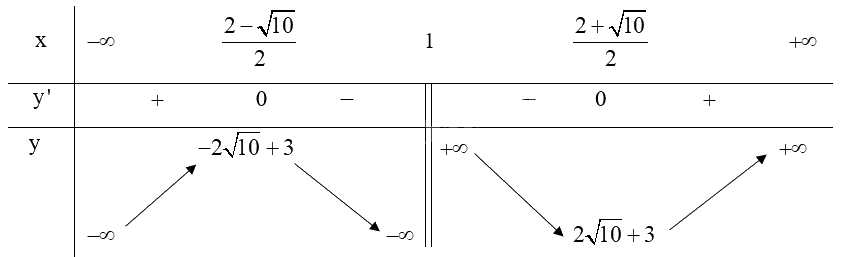
\(y' = 2 - \frac{5}{{{{\left( {x - 1} \right)}^2}}},y' = 0 \Leftrightarrow x = \frac{{2 - \sqrt {10} }}{2}\) hoặc \(x = \frac{{2 + \sqrt {10} }}{2}\)
Trong khoảng \(\left( { - \infty ;\frac{{2 - \sqrt {10} }}{2}} \right)\) và \(\left( {\frac{{2 + \sqrt {10} }}{2}; + \infty } \right)\), \(y' > 0\) nên hàm số đồng biến.
Trong khoảng \(\left( {\frac{{2 - \sqrt {10} }}{2};1} \right)\) và \(\left( {1;\frac{{2 + \sqrt {10} }}{2}} \right)\), \(y' < 0\) nên hàm số nghịch biến.
Hàm số đạt cực đại tại \(x = \frac{{2 - \sqrt {10} }}{2}\), giá trị cực đại .
Hàm số đạt cực tiểu tại \(x = \frac{{2 + \sqrt {10} }}{2}\), giá trị cực đại \({y_{CT}} = 2\sqrt {10} + 3\).
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - x + 4}}{{x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{2{x^2} - x + 4}}{{x - 1}} = - \infty \) \(\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{2{x^2} - x + 4}}{{x - 1}} = - \infty ;\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{2{x^2} - x + 4}}{{x - 1}} = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {2x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left( {2x + 1 + \frac{5}{{x - 1}} - \left( {2x + 1} \right)} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{5}{{x - 1}} = 0\)
\(\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {2x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \left( {2x + 1 + \frac{5}{{x - 1}} - \left( {2x + 1} \right)} \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{5}{{x - 1}} = 0\)
Do đó, đồ thị hàm số nhận đường thẳng \(x = 1\) làm tiệm cận đứng và đường thẳng \(y = 2x + 1\) làm tiệm cận xiên.
Bảng biến thiên:
3. Đồ thị:
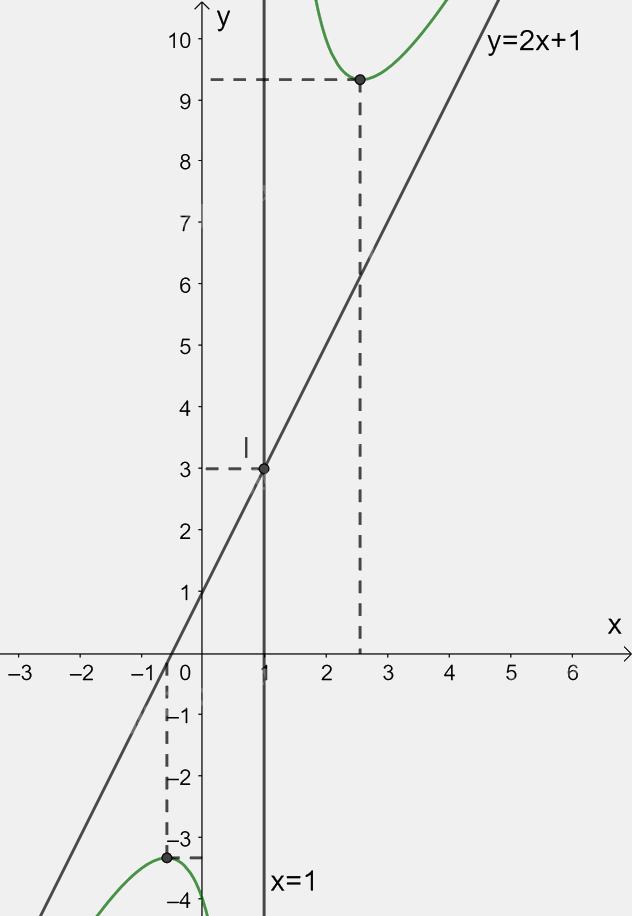
Giao điểm của đồ thị hàm số với trục tung là (0; -4).
Đồ thị hàm số không cắt trục Ox.
Đồ thị hàm số nhận giao điểm I(1; 3) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
b) \(y = \frac{{{x^2} + 2x + 1}}{{x + 3}}\)
1. Tập xác định của hàm số: \(\mathbb{R}\backslash \left\{ { - 3} \right\}\)
2. Sự biến thiên:
Ta có: \(y = \frac{{{x^2} + 2x + 1}}{{x + 3}} = x - 1 + \frac{4}{{x + 3}}\)
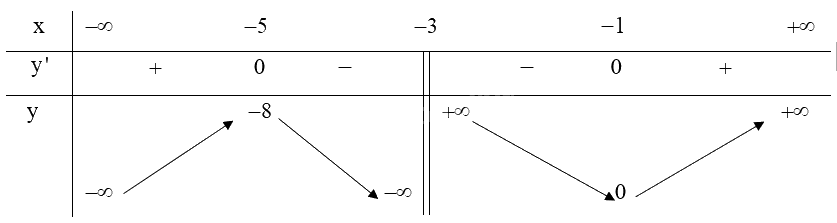
\(y' = 1 - \frac{4}{{{{\left( {x + 3} \right)}^2}}},y' = 0 \Leftrightarrow x = - 1\) hoặc \(x = - 5\).
Trong khoảng \(\left( { - \infty ; - 5} \right)\) và \(\left( { - 1; + \infty } \right)\), \(y' > 0\) nên hàm số đồng biến.
Trong khoảng \(\left( { - 5; - 3} \right)\) và \(\left( { - 3; - 1} \right)\), \(y' < 0\) nên hàm số nghịch biến.
Hàm số đạt cực đại tại \(x = - 5\), giá trị cực đại .
Hàm số đạt cực tiểu tại \(x = - 1\), giá trị cực tiểu \({y_{CT}} = 0\).
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} + 2x + 1}}{{x + 3}} = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + 2x + 1}}{{x + 3}} = - \infty \) \(\mathop {\lim }\limits_{x \to - {3^ - }} y = \mathop {\lim }\limits_{x \to - {3^ - }} \frac{{{x^2} + 2x + 1}}{{x + 3}} = - \infty ;\mathop {\lim }\limits_{x \to - {3^ + }} y = \mathop {\lim }\limits_{x \to - {3^ + }} \frac{{{x^2} + 2x + 1}}{{x + 3}} = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left( {x - 1 + \frac{4}{{x + 3}} - \left( {x - 1} \right)} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{4}{{x + 3}} = 0\)
\(\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \left( {x - 1 + \frac{4}{{x + 3}} - \left( {x - 1} \right)} \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{4}{{x + 3}} = 0\)
Do đó, đồ thị hàm số nhận đường thẳng \(x = - 3\) làm tiệm cận đứng và đường thẳng \(y = x - 1\) làm tiệm cận xiên.
Bảng biến thiên:
3. Đồ thị:
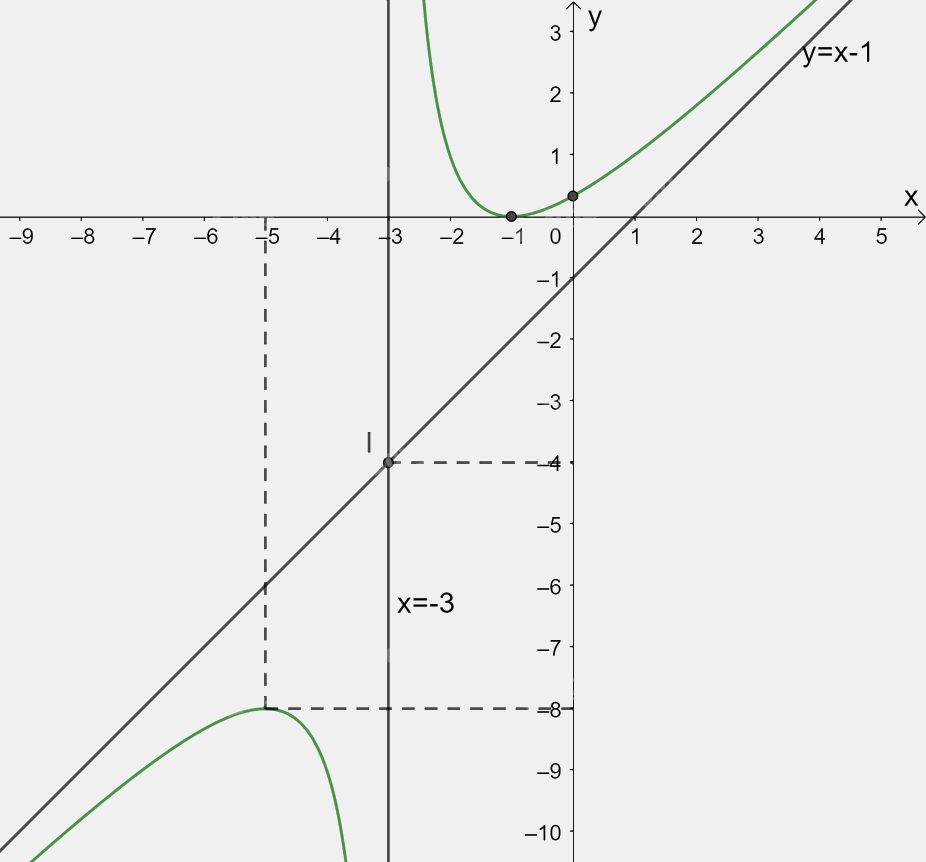
Giao điểmcủa đồ thị hàm số với trục tung là \(\left( {0;\frac{1}{3}} \right)\).
\(y = 0 \Leftrightarrow \frac{{{x^2} + 2x + 1}}{{x + 3}} = 0 \Leftrightarrow x = - 1\)
Giao điểm của đồ thị hàm số với trục hoành là điểm \(\left( { - 1;0} \right)\).
Đồ thị hàm số nhận giao điểm \(I\left( { - 3; - 4} \right)\) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
Bài tập 1.23 trang 32 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương trình học về giới hạn của hàm số. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các định lý liên quan và các phương pháp tính giới hạn thường gặp.
(Nội dung đề bài sẽ được chèn vào đây - ví dụ: Tính giới hạn sau: lim (x->2) (x^2 - 4) / (x - 2))
Trước khi bắt tay vào giải bài tập, chúng ta cần phân tích đề bài để xác định phương pháp giải phù hợp. Trong trường hợp này, biểu thức giới hạn có dạng vô định 0/0 khi x tiến tới 2. Do đó, chúng ta có thể sử dụng phương pháp phân tích tử và mẫu thành nhân tử để rút gọn biểu thức và tính giới hạn.
(Lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải cụ thể, giải thích rõ ràng và kết luận.)
Để củng cố kiến thức về giới hạn, bạn có thể tham khảo thêm các bài tập tương tự trong SGK Toán 12 tập 1 - Kết nối tri thức. Ngoài ra, bạn cũng có thể tìm kiếm các tài liệu tham khảo khác trên mạng hoặc tại các thư viện để nâng cao khả năng giải toán của mình.
Giới hạn là một khái niệm quan trọng trong toán học và có nhiều ứng dụng trong thực tế, chẳng hạn như trong vật lý, kinh tế, kỹ thuật. Ví dụ, giới hạn được sử dụng để tính vận tốc tức thời của một vật thể, để tính lãi suất kép, để tính độ chính xác của một phép đo.
Các dạng bài tập giới hạn thường gặp bao gồm:
Hiện nay, có rất nhiều công cụ hỗ trợ giải toán online có thể giúp bạn giải các bài tập về giới hạn một cách nhanh chóng và chính xác. Tuy nhiên, bạn nên sử dụng các công cụ này một cách cẩn thận và không nên lạm dụng chúng. Thay vào đó, bạn nên cố gắng tự giải bài tập để hiểu rõ bản chất của bài toán.
Bài tập 1.23 trang 32 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập cơ bản về giới hạn. Hy vọng rằng, với lời giải chi tiết và các hướng dẫn trên, bạn đã có thể hiểu rõ cách giải bài tập này và củng cố kiến thức về giới hạn. Chúc bạn học tập tốt!
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.