Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 54, 55, 56 sách giáo khoa Toán 12 tập 2 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
PHƯƠNG TRÌNH MẶT CẦU
Trả lời câu hỏi Luyện tập 2 trang 55 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, viết phương trình mặt cầu (S) trong các trường hợp sau:
a) Tâm là gốc tọa độ, bán kính \(R = 1\).
b) Đường kính AB, với \(A\left( {1; - 1;2} \right),B\left( {2; - 3; - 1} \right)\).
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để viết phương trình mặt cầu: Trong không gian Oxyz, mặt cầu (S) tâm I(a; b; c), bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Lời giải chi tiết:
a) Mặt cầu (S) có tâm \(O\left( {0;0;0} \right)\), bán kính \(R = 1\) nên có phương trình là: \({x^2} + {y^2} + {z^2} = 1\)
b) Đoạn thẳng AB có trung điểm là \(E\left( {\frac{3}{2}; - 2;\frac{1}{2}} \right)\).
Mặt cầu (S) có bán kính \(R = \frac{1}{2}AB = \frac{1}{2}\sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( { - 3 + 1} \right)}^2} + {{\left( { - 1 - 2} \right)}^2}} = \frac{{\sqrt {14} }}{2}\) và tâm \(E\left( {\frac{3}{2}; - 2;\frac{1}{2}} \right)\). Do đó, (S): \({\left( {x - \frac{3}{2}} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - \frac{1}{2}} \right)^2} = \frac{7}{2}\)
Trả lời câu hỏi Luyện tập 1 trang 55 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt cầu (S) có phương trình \({\left( {x + 2} \right)^2} + {y^2} + {\left( {z + \frac{1}{2}} \right)^2} = \frac{9}{4}\).
a) Xác định tâm và bán kính của (S).
b) Hỏi điểm \(M\left( {2;0;1} \right)\) nằm trong, nằm ngoài hay thuộc mặt cầu (S)?
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để xác định tâm và bán kính của mặt cầu: Trong không gian Oxyz, mặt cầu (S) tâm \(I\left( {a;{\rm{ }}b;{\rm{ }}c} \right)\), bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Sử dụng kiến thức về phương trình mặt cầu để xác định vị trí của điểm so với mặt cầu: Cho mặt cầu (S) tâm I, bán kính R và điểm M bất kì trong không gian:
+ Nếu \(IM = R\) thì M nằm trên mặt cầu (S) tâm I.
+ Nếu \(IM > R\) thì M nằm ngoài mặt cầu (S) tâm I.
+ Nếu \(IM < R\) thì M nằm trong mặt cầu (S) tâm I.
Lời giải chi tiết:
a) Ta viết lại phương trình mặt cầu (S) dưới dạng:
\({\left[ {x - \left( { - 2} \right)} \right]^2} + {\left( {y - 0} \right)^2} + {\left[ {z - \left( { - \frac{1}{2}} \right)} \right]^2} = {\left( {\frac{3}{2}} \right)^2}\)
Do đó, mặt cầu (S) có tâm \(I\left( { - 2;0;\frac{{ - 1}}{2}} \right)\) và bán kính \(R = \frac{3}{2}\).
b) Ta có: \(MI = \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( {0 - 0} \right)}^2} + {{\left( {\frac{{ - 1}}{2} - 1} \right)}^2}} = \frac{{\sqrt {73} }}{2} > \frac{3}{2} = R\) nên điểm \(M\left( {2;0;1} \right)\) nằm ngoài mặt cầu (S).
Trả lời câu hỏi Luyện tập 3 trang 56 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho (S) là tập hợp các điểm \(M\left( {x;{\rm{ }}y;{\rm{ }}z} \right)\) có tọa độ thỏa mãn phương trình: \({x^2} + {y^2} + {z^2} - 4x + 6y - 12 = 0\). Chứng minh rằng (S) là một mặt cầu. Xác định tâm và bán kính của mặt cầu đó.
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để chứng minh: Trong không gian Oxyz, mặt cầu (S) tâm \(I\left( {a;b;c} \right),\) bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)
Lời giải chi tiết:
Ta có: \({x^2} + {y^2} + {z^2} - 4x + 6y - 12 = 0\)
\( \Leftrightarrow \left( {{x^2} - 4x + 4} \right) + \left( {{y^2} + 6y + 9} \right) + {z^2} = 25\)\( \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} + {z^2} = {5^2}\)
Do đó, (S) là mặt cầu có tâm \(I\left( {2; - 3;0} \right)\) và bán kính \(R = 5\).
Trả lời câu hỏi Luyện tập 4 trang 56 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt cầu (S) có phương trình:
\({x^2} + {y^2} + {z^2} + 4x - 5y + 6z + \frac{{25}}{4} = 0\).
Xác định tâm, tính bán kính của (S).
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để tính: Với a, b, c, d là các hằng số, phương trình \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) có thể viết lại thành \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {a^2} + {b^2} + {c^2} - d\) và là phương trình của một mặt cầu (S) khi và chỉ khi \({a^2} + {b^2} + {c^2} - d > 0\). Khi đó, (S) có tâm \(I\left( {a;{\rm{ }}b;{\rm{ }}c} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \).
Lời giải chi tiết:
Phương trình mặt cầu (S) đã cho tương ứng với \(a = - 2;b = \frac{5}{2};c = - 3,d = \frac{{25}}{4}\)
Nên mặt cầu (S) có tâm \(I\left( { - 2;\frac{5}{2}; - 3} \right)\), bán kính \(R = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( {\frac{5}{2}} \right)}^2} + {{\left( { - 3} \right)}^2} - \frac{{25}}{4}} = \sqrt {13} \)
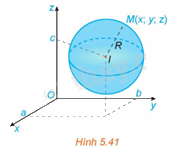
Trả lời câu hỏi Hoạt động 1 trang 54 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt cầu (S) tâm và bán kính R (H.5.41). Khi đó, một điểm thuộc mặt cầu (S) khi và chỉ khi nó thỏa mãn điều kiện gì?
Phương pháp giải:
Sử dụng kiến thức về mặt cầu tâm để tìm điều kiện:
+ Mặt cầu tâm I bán kính R là tập hợp các điểm trong không gian cách I một khoảng bằng R.
+ Mỗi đường thẳng đi qua tâm mặt cầu đều cắt mặt cầu tại hai điểm phân biệt, đoạn thẳng nối hai điểm đó được gọi là đường kính mặt cầu. Mỗi đường kính của mặt cầu đều có trung điểm là tâm mặt cầu và có độ dài bằng hai lần bán kính mặt cầu.
Lời giải chi tiết:
Mặt cầu tâm I bán kính R là tập hợp các điểm trong không gian cách I một khoảng bằng R.
Do đó, điểm thuộc mặt cầu (S) khi và chỉ khi .
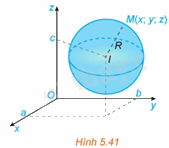
Trả lời câu hỏi Hoạt động 1 trang 54 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt cầu (S) tâm và bán kính R (H.5.41). Khi đó, một điểm thuộc mặt cầu (S) khi và chỉ khi nó thỏa mãn điều kiện gì?
Phương pháp giải:
Sử dụng kiến thức về mặt cầu tâm để tìm điều kiện:
+ Mặt cầu tâm I bán kính R là tập hợp các điểm trong không gian cách I một khoảng bằng R.
+ Mỗi đường thẳng đi qua tâm mặt cầu đều cắt mặt cầu tại hai điểm phân biệt, đoạn thẳng nối hai điểm đó được gọi là đường kính mặt cầu. Mỗi đường kính của mặt cầu đều có trung điểm là tâm mặt cầu và có độ dài bằng hai lần bán kính mặt cầu.
Lời giải chi tiết:
Mặt cầu tâm I bán kính R là tập hợp các điểm trong không gian cách I một khoảng bằng R.
Do đó, điểm thuộc mặt cầu (S) khi và chỉ khi .
Trả lời câu hỏi Luyện tập 1 trang 55 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt cầu (S) có phương trình \({\left( {x + 2} \right)^2} + {y^2} + {\left( {z + \frac{1}{2}} \right)^2} = \frac{9}{4}\).
a) Xác định tâm và bán kính của (S).
b) Hỏi điểm \(M\left( {2;0;1} \right)\) nằm trong, nằm ngoài hay thuộc mặt cầu (S)?
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để xác định tâm và bán kính của mặt cầu: Trong không gian Oxyz, mặt cầu (S) tâm \(I\left( {a;{\rm{ }}b;{\rm{ }}c} \right)\), bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Sử dụng kiến thức về phương trình mặt cầu để xác định vị trí của điểm so với mặt cầu: Cho mặt cầu (S) tâm I, bán kính R và điểm M bất kì trong không gian:
+ Nếu \(IM = R\) thì M nằm trên mặt cầu (S) tâm I.
+ Nếu \(IM > R\) thì M nằm ngoài mặt cầu (S) tâm I.
+ Nếu \(IM < R\) thì M nằm trong mặt cầu (S) tâm I.
Lời giải chi tiết:
a) Ta viết lại phương trình mặt cầu (S) dưới dạng:
\({\left[ {x - \left( { - 2} \right)} \right]^2} + {\left( {y - 0} \right)^2} + {\left[ {z - \left( { - \frac{1}{2}} \right)} \right]^2} = {\left( {\frac{3}{2}} \right)^2}\)
Do đó, mặt cầu (S) có tâm \(I\left( { - 2;0;\frac{{ - 1}}{2}} \right)\) và bán kính \(R = \frac{3}{2}\).
b) Ta có: \(MI = \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( {0 - 0} \right)}^2} + {{\left( {\frac{{ - 1}}{2} - 1} \right)}^2}} = \frac{{\sqrt {73} }}{2} > \frac{3}{2} = R\) nên điểm \(M\left( {2;0;1} \right)\) nằm ngoài mặt cầu (S).
Trả lời câu hỏi Luyện tập 2 trang 55 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, viết phương trình mặt cầu (S) trong các trường hợp sau:
a) Tâm là gốc tọa độ, bán kính \(R = 1\).
b) Đường kính AB, với \(A\left( {1; - 1;2} \right),B\left( {2; - 3; - 1} \right)\).
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để viết phương trình mặt cầu: Trong không gian Oxyz, mặt cầu (S) tâm I(a; b; c), bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Lời giải chi tiết:
a) Mặt cầu (S) có tâm \(O\left( {0;0;0} \right)\), bán kính \(R = 1\) nên có phương trình là: \({x^2} + {y^2} + {z^2} = 1\)
b) Đoạn thẳng AB có trung điểm là \(E\left( {\frac{3}{2}; - 2;\frac{1}{2}} \right)\).
Mặt cầu (S) có bán kính \(R = \frac{1}{2}AB = \frac{1}{2}\sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( { - 3 + 1} \right)}^2} + {{\left( { - 1 - 2} \right)}^2}} = \frac{{\sqrt {14} }}{2}\) và tâm \(E\left( {\frac{3}{2}; - 2;\frac{1}{2}} \right)\). Do đó, (S): \({\left( {x - \frac{3}{2}} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - \frac{1}{2}} \right)^2} = \frac{7}{2}\)
Trả lời câu hỏi Luyện tập 3 trang 56 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho (S) là tập hợp các điểm \(M\left( {x;{\rm{ }}y;{\rm{ }}z} \right)\) có tọa độ thỏa mãn phương trình: \({x^2} + {y^2} + {z^2} - 4x + 6y - 12 = 0\). Chứng minh rằng (S) là một mặt cầu. Xác định tâm và bán kính của mặt cầu đó.
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để chứng minh: Trong không gian Oxyz, mặt cầu (S) tâm \(I\left( {a;b;c} \right),\) bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)
Lời giải chi tiết:
Ta có: \({x^2} + {y^2} + {z^2} - 4x + 6y - 12 = 0\)
\( \Leftrightarrow \left( {{x^2} - 4x + 4} \right) + \left( {{y^2} + 6y + 9} \right) + {z^2} = 25\)\( \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} + {z^2} = {5^2}\)
Do đó, (S) là mặt cầu có tâm \(I\left( {2; - 3;0} \right)\) và bán kính \(R = 5\).
Trả lời câu hỏi Luyện tập 4 trang 56 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt cầu (S) có phương trình:
\({x^2} + {y^2} + {z^2} + 4x - 5y + 6z + \frac{{25}}{4} = 0\).
Xác định tâm, tính bán kính của (S).
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để tính: Với a, b, c, d là các hằng số, phương trình \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) có thể viết lại thành \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {a^2} + {b^2} + {c^2} - d\) và là phương trình của một mặt cầu (S) khi và chỉ khi \({a^2} + {b^2} + {c^2} - d > 0\). Khi đó, (S) có tâm \(I\left( {a;{\rm{ }}b;{\rm{ }}c} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \).
Lời giải chi tiết:
Phương trình mặt cầu (S) đã cho tương ứng với \(a = - 2;b = \frac{5}{2};c = - 3,d = \frac{{25}}{4}\)
Nên mặt cầu (S) có tâm \(I\left( { - 2;\frac{5}{2}; - 3} \right)\), bán kính \(R = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( {\frac{5}{2}} \right)}^2} + {{\left( { - 3} \right)}^2} - \frac{{25}}{4}} = \sqrt {13} \)
Mục 1 của chương trình Toán 12 tập 2 Kết nối tri thức thường tập trung vào một chủ đề quan trọng, thường là về đạo hàm hoặc tích phân. Việc nắm vững kiến thức trong mục này là nền tảng để giải quyết các bài toán phức tạp hơn trong các chương tiếp theo. Bài viết này sẽ đi sâu vào từng bài tập trong trang 54, 55 và 56, cung cấp lời giải chi tiết, phân tích từng bước và giải thích rõ ràng các khái niệm liên quan.
Trang 54 thường chứa các bài tập áp dụng kiến thức cơ bản về đạo hàm của hàm số. Các bài tập này thường yêu cầu học sinh tính đạo hàm của các hàm số đơn giản, hoặc tìm đạo hàm cấp hai. Để giải các bài tập này, học sinh cần nắm vững các quy tắc tính đạo hàm cơ bản, như quy tắc đạo hàm của tổng, hiệu, tích, thương và quy tắc đạo hàm của hàm hợp.
Cho hàm số f(x) = x3 + 2x2 - 5x + 1. Tính f'(x).
Lời giải:
Trang 55 thường chứa các bài tập về ứng dụng của đạo hàm để xét tính đơn điệu của hàm số. Các bài tập này yêu cầu học sinh tìm đạo hàm của hàm số, xét dấu đạo hàm và kết luận về tính đơn điệu của hàm số trên các khoảng xác định.
Xét hàm số f(x) = x2 - 4x + 3. Tìm khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
Trang 56 thường chứa các bài tập về cực trị của hàm số. Các bài tập này yêu cầu học sinh tìm đạo hàm bậc nhất, tìm các điểm làm đạo hàm bậc nhất bằng 0, xét dấu đạo hàm bậc nhất để xác định cực đại, cực tiểu của hàm số.
Tìm cực đại, cực tiểu của hàm số f(x) = x3 - 3x2 + 2.
Lời giải:
Hy vọng bài viết này sẽ giúp các em học sinh giải quyết các bài tập trong mục 1 trang 54, 55, 56 SGK Toán 12 tập 2 Kết nối tri thức một cách hiệu quả. Chúc các em học tốt!