Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 65, 66, 67 sách giáo khoa Toán 12 tập 2 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học.
XÁC SUẤT CÓ ĐIỀU KIỆN
Trả lời câu hỏi Luyện tập 1 trang 66 SGK Toán 12 Kết nối tri thức
Trở lại Ví dụ 1. Tính \(P\left( {A|\overline B } \right)\) bằng định nghĩa và bằng công thức.
Phương pháp giải:
Sử dụng kiến thức về định nghĩa xác suất có điều kiện để tính: Cho hai biến cố A và B. Xác suất của biến cố A, tính trong điều kiện biết rằng nếu biến cố B đã xảy ra, được gọi là xác suất của A với điều kiện B và kí hiệu là \(P\left( {A|B} \right)\).
Sử dụng kiến thức về công thức tính xác suất có điều kiện để tính: Cho hai biến cố A và B bất kì, với \(P\left( B \right) > 0\). Khi đó, \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}}\)
Lời giải chi tiết:
Cách 1: Bằng định nghĩa
Nếu \(\overline B \) xảy ra tức là Bình lấy được viên bi đen. Khi đó, trong hộp còn lại 29 viên bi với 20 viên bi trắng và 9 viên bi đen. Vậy \(P\left( {A|\overline B } \right) = \frac{{20}}{{29}}\).
Cách 2: Bằng công thức
Bình có 30 cách chọn, An có 29 cách chọn một viên bi trong hộp. Do đó, \(n\left( \Omega \right) = 30.29\)
Bình có 10 cách chọn một viên bi đen, An có 29 cách chọn từ 29 viên bi còn lại.
Do đó, \(n\left( {\overline B } \right) = 10.29\) và \(P\left( {\overline B } \right) = \frac{{n\left( {\overline B } \right)}}{{n\left( \Omega \right)}}\)
Bình có 10 cách chọn một viên bi đen, An có 20 cách chọn một viên bi trắng. Do đó, \(n\left( {A\overline B } \right) = 10.20\) và \(P\left( {\overline B } \right) = \frac{{n\left( {A\overline B } \right)}}{{n\left( \Omega \right)}}\)
Vậy \(P\left( {A|\overline B } \right) = \frac{{n\left( {A\overline B } \right)}}{{n\left( {\overline B } \right)}} = \frac{{10.20}}{{10.29}} = \frac{{20}}{{29}}\)
Trả lời câu hỏi Hoạt động 1 trang 65 SGK Toán 12 Kết nối tri thức
Trong một hộp kín có 7 chiếc bút bi xanh và 5 chiếc bút bi đen, các chiếc bút có cùng kích thước và khối lượng. Bạn Sơn lấy ngẫu nhiên một chiếc bút trong hộp, không trả lại. Sau đó, Tùng lấy ngẫu nhiên 1 trong 11 chiếc bút còn lại. Tính xác suất để Tùng lấy được bút bi xanh nếu biết rằng Sơn đã lấy được bút bi đen.
Phương pháp giải:
Sử dụng kiến thức về quy tắc nhân hai biến cố độc lập để tính: Nếu A và B độc lập thì \(P\left( {AB} \right) = P\left( A \right).P\left( B \right)\).
Lời giải chi tiết:
Gọi A là biến cố: “Tùng lấy được bút bi xanh”, B là biến cố: “Sơn lấy được bút bi đen”.
Sơn có 12 cách chọn, Tùng có 11 cách chọn một chiếc bút bi trong hộp.
Do đó, \(n\left( \Omega \right) = 12.11 = 132\)
Sơn có 5 cách chọn bút bi đen, Tùng có 11 cách chọn bút bi xanh từ 11 bút bi còn lại.
Do đó, \(n\left( B \right) = 5.11 = 55\) và \(P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}}\)
Sơn có 5 cách chọn bút bi đen, Tùng có 7 cách chọn bút bi xanh từ 11 bút bi còn lại.
Do đó, \(n\left( {AB} \right) = 5.7 = 35\) và \(P\left( {AB} \right) = \frac{{n\left( {AB} \right)}}{{n\left( \Omega \right)}}\)
Vậy xác suất để Tùng lấy được bút bi xanh nếu Sơn lấy được bút bi đen là: \(P = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{n\left( {AB} \right)}}{{n\left( B \right)}} = \frac{{35}}{{55}} = \frac{7}{{11}}\)
Trả lời câu hỏi Luyện tập 2 trang 66 SGK Toán 12 Kết nối tri thức
Chứng tỏ rằng nếu A và B là hai biến cố độc lập thì \(P\left( {\overline A |B} \right) = P\left( {\overline A } \right)\) và \(P\left( {A|\overline B } \right) = P\left( A \right)\)
Phương pháp giải:
Sử dụng kiến thức về định nghĩa xác suất có điều kiện để chứng minh: Cho hai biến cố A và B. Xác suất của biến cố A, tính trong điều kiện biết rằng nếu biến cố B đã xảy ra, được gọi là xác suất của A với điều kiện B và kí hiệu là \(P\left( {A|B} \right)\).
Sử dụng kiến thức về tính chất biến cố độc lập để chứng minh: Nếu cặp biến cố A và B độc lập thì cặp biến cố \(\overline A \) và B; A và \(\overline B \) cũng độc lập.
Sử dụng kiến thức về công thức tính xác suất có điều kiện để tính: Cho hai biến cố A và B bất kì, với \(P\left( B \right) > 0\). Khi đó, \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}}\).
Lời giải chi tiết:
Theo định nghĩa, \(P\left( {\overline A |B} \right)\) là xác suất của \(\overline A \), tính trong điều kiện biết rằng nếu biến cố B đã xảy ra. Vì A và B độc lập nên \(\overline A \) và B cũng độc lập. Do đó, việc xảy ra B không ảnh hưởng tới xác suất xuất hiện của \(\overline A \). Do đó, \(P\left( {\overline A |B} \right) = P\left( {\overline A } \right)\).
Theo định nghĩa, \(P\left( {A|\overline B } \right) = P\left( A \right)\) là xác suất của A, tính trong điều kiện biết rằng nếu biến cố \(\overline B \) đã xảy ra. Vì A và B độc lập nên A và \(\overline B \) cũng độc lập. Do đó, việc xảy ra \(\overline B \) không ảnh hưởng tới xác suất xuất hiện của A. Do đó, \(P\left( {A|\overline B } \right) = P\left( A \right)\).
Trả lời câu hỏi Luyện tập 3 trang 68 SGK Toán 12 Kết nối tri thức
Một công ty dược phẩm muốn so sánh tác dụng điều trị bệnh X của hai loại thuốc M và N. Công ty đã tiến hành thử nghiệm với 4 000 bệnh nhân mắc bệnh X trong đó 2 400 bệnh nhân dùng thuốc M, 1 600 bệnh nhân còn lại dùng thuốc N. Kết quả được cho trong bảng dữ liệu thống kê \(2 \times 2\) như sau:
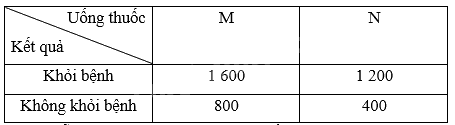
Chọn ngẫu nhiên một bệnh nhân trong số 4 000 bệnh nhân thử nghiệm sau khi uống thuốc. Tính xác suất để bệnh nhân đó
a) uống thuốc M, biết rằng bệnh nhân đó khỏi bệnh;
b) uống thuốc N, biết rằng bệnh nhân đó không khỏi bệnh.
Phương pháp giải:
Sử dụng kiến thức về công thức tính xác suất có điều kiện để tính: Cho hai biến cố A và B bất kì, với \(P\left( B \right) > 0\). Khi đó, \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}}\).
Lời giải chi tiết:
Không gian mẫu \(\Omega \) là tập hợp gồm 4 000 bệnh nhân thử nghiệm nên \(n\left( \Omega \right) = 4000\)
a) Gọi A là biến cố: “Người đó uống thuốc M”, B là biến cố “Người đó khỏi bệnh”
Khi đó biến cố AB là: “Người đó uống thuốc M và khỏi bệnh”
Ta có: \(1600 + 1200 = 2800\) người khỏi bệnh nên \(n\left( B \right) = 2800\). Do đó, \(P\left( B \right) = \frac{{2800}}{{4000}}\)
Trong số những người khỏi bệnh, có 1 600 người uống thuốc M nên \(n\left( {AB} \right) = 1\;600\)
Do đó, \(P\left( {AB} \right) = \frac{{1600}}{{4000}}\). Vậy \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{1600}}{{2800}} = \frac{4}{7}\)
b) Gọi A là biến cố: “Người đó uống thuốc N”, B là biến cố “Người đó không khỏi bệnh”.
Khi đó biến cố AB là: “Người đó uống thuốc N và không khỏi bệnh”
Ta có: \(800 + 400 = 1200\) người không khỏi bệnh nên \(n\left( B \right) = 1200\). Do đó, \(P\left( B \right) = \frac{{1200}}{{4000}}\)
Trong số những người không khỏi bệnh, có 400 người uống thuốc N nên \(n\left( {AB} \right) = 400\)
Do đó, \(P\left( {AB} \right) = \frac{{400}}{{4000}}\). Vậy \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{400}}{{1200}} = \frac{1}{3}\)
Trả lời câu hỏi Hoạt động 1 trang 65 SGK Toán 12 Kết nối tri thức
Trong một hộp kín có 7 chiếc bút bi xanh và 5 chiếc bút bi đen, các chiếc bút có cùng kích thước và khối lượng. Bạn Sơn lấy ngẫu nhiên một chiếc bút trong hộp, không trả lại. Sau đó, Tùng lấy ngẫu nhiên 1 trong 11 chiếc bút còn lại. Tính xác suất để Tùng lấy được bút bi xanh nếu biết rằng Sơn đã lấy được bút bi đen.
Phương pháp giải:
Sử dụng kiến thức về quy tắc nhân hai biến cố độc lập để tính: Nếu A và B độc lập thì \(P\left( {AB} \right) = P\left( A \right).P\left( B \right)\).
Lời giải chi tiết:
Gọi A là biến cố: “Tùng lấy được bút bi xanh”, B là biến cố: “Sơn lấy được bút bi đen”.
Sơn có 12 cách chọn, Tùng có 11 cách chọn một chiếc bút bi trong hộp.
Do đó, \(n\left( \Omega \right) = 12.11 = 132\)
Sơn có 5 cách chọn bút bi đen, Tùng có 11 cách chọn bút bi xanh từ 11 bút bi còn lại.
Do đó, \(n\left( B \right) = 5.11 = 55\) và \(P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}}\)
Sơn có 5 cách chọn bút bi đen, Tùng có 7 cách chọn bút bi xanh từ 11 bút bi còn lại.
Do đó, \(n\left( {AB} \right) = 5.7 = 35\) và \(P\left( {AB} \right) = \frac{{n\left( {AB} \right)}}{{n\left( \Omega \right)}}\)
Vậy xác suất để Tùng lấy được bút bi xanh nếu Sơn lấy được bút bi đen là: \(P = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{n\left( {AB} \right)}}{{n\left( B \right)}} = \frac{{35}}{{55}} = \frac{7}{{11}}\)
Trả lời câu hỏi Luyện tập 1 trang 66 SGK Toán 12 Kết nối tri thức
Trở lại Ví dụ 1. Tính \(P\left( {A|\overline B } \right)\) bằng định nghĩa và bằng công thức.
Phương pháp giải:
Sử dụng kiến thức về định nghĩa xác suất có điều kiện để tính: Cho hai biến cố A và B. Xác suất của biến cố A, tính trong điều kiện biết rằng nếu biến cố B đã xảy ra, được gọi là xác suất của A với điều kiện B và kí hiệu là \(P\left( {A|B} \right)\).
Sử dụng kiến thức về công thức tính xác suất có điều kiện để tính: Cho hai biến cố A và B bất kì, với \(P\left( B \right) > 0\). Khi đó, \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}}\)
Lời giải chi tiết:
Cách 1: Bằng định nghĩa
Nếu \(\overline B \) xảy ra tức là Bình lấy được viên bi đen. Khi đó, trong hộp còn lại 29 viên bi với 20 viên bi trắng và 9 viên bi đen. Vậy \(P\left( {A|\overline B } \right) = \frac{{20}}{{29}}\).
Cách 2: Bằng công thức
Bình có 30 cách chọn, An có 29 cách chọn một viên bi trong hộp. Do đó, \(n\left( \Omega \right) = 30.29\)
Bình có 10 cách chọn một viên bi đen, An có 29 cách chọn từ 29 viên bi còn lại.
Do đó, \(n\left( {\overline B } \right) = 10.29\) và \(P\left( {\overline B } \right) = \frac{{n\left( {\overline B } \right)}}{{n\left( \Omega \right)}}\)
Bình có 10 cách chọn một viên bi đen, An có 20 cách chọn một viên bi trắng. Do đó, \(n\left( {A\overline B } \right) = 10.20\) và \(P\left( {\overline B } \right) = \frac{{n\left( {A\overline B } \right)}}{{n\left( \Omega \right)}}\)
Vậy \(P\left( {A|\overline B } \right) = \frac{{n\left( {A\overline B } \right)}}{{n\left( {\overline B } \right)}} = \frac{{10.20}}{{10.29}} = \frac{{20}}{{29}}\)
Trả lời câu hỏi Luyện tập 2 trang 66 SGK Toán 12 Kết nối tri thức
Chứng tỏ rằng nếu A và B là hai biến cố độc lập thì \(P\left( {\overline A |B} \right) = P\left( {\overline A } \right)\) và \(P\left( {A|\overline B } \right) = P\left( A \right)\)
Phương pháp giải:
Sử dụng kiến thức về định nghĩa xác suất có điều kiện để chứng minh: Cho hai biến cố A và B. Xác suất của biến cố A, tính trong điều kiện biết rằng nếu biến cố B đã xảy ra, được gọi là xác suất của A với điều kiện B và kí hiệu là \(P\left( {A|B} \right)\).
Sử dụng kiến thức về tính chất biến cố độc lập để chứng minh: Nếu cặp biến cố A và B độc lập thì cặp biến cố \(\overline A \) và B; A và \(\overline B \) cũng độc lập.
Sử dụng kiến thức về công thức tính xác suất có điều kiện để tính: Cho hai biến cố A và B bất kì, với \(P\left( B \right) > 0\). Khi đó, \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}}\).
Lời giải chi tiết:
Theo định nghĩa, \(P\left( {\overline A |B} \right)\) là xác suất của \(\overline A \), tính trong điều kiện biết rằng nếu biến cố B đã xảy ra. Vì A và B độc lập nên \(\overline A \) và B cũng độc lập. Do đó, việc xảy ra B không ảnh hưởng tới xác suất xuất hiện của \(\overline A \). Do đó, \(P\left( {\overline A |B} \right) = P\left( {\overline A } \right)\).
Theo định nghĩa, \(P\left( {A|\overline B } \right) = P\left( A \right)\) là xác suất của A, tính trong điều kiện biết rằng nếu biến cố \(\overline B \) đã xảy ra. Vì A và B độc lập nên A và \(\overline B \) cũng độc lập. Do đó, việc xảy ra \(\overline B \) không ảnh hưởng tới xác suất xuất hiện của A. Do đó, \(P\left( {A|\overline B } \right) = P\left( A \right)\).
Trả lời câu hỏi Luyện tập 3 trang 68 SGK Toán 12 Kết nối tri thức
Một công ty dược phẩm muốn so sánh tác dụng điều trị bệnh X của hai loại thuốc M và N. Công ty đã tiến hành thử nghiệm với 4 000 bệnh nhân mắc bệnh X trong đó 2 400 bệnh nhân dùng thuốc M, 1 600 bệnh nhân còn lại dùng thuốc N. Kết quả được cho trong bảng dữ liệu thống kê \(2 \times 2\) như sau:
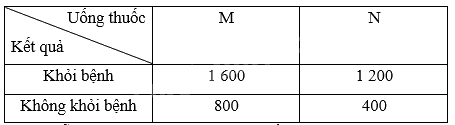
Chọn ngẫu nhiên một bệnh nhân trong số 4 000 bệnh nhân thử nghiệm sau khi uống thuốc. Tính xác suất để bệnh nhân đó
a) uống thuốc M, biết rằng bệnh nhân đó khỏi bệnh;
b) uống thuốc N, biết rằng bệnh nhân đó không khỏi bệnh.
Phương pháp giải:
Sử dụng kiến thức về công thức tính xác suất có điều kiện để tính: Cho hai biến cố A và B bất kì, với \(P\left( B \right) > 0\). Khi đó, \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}}\).
Lời giải chi tiết:
Không gian mẫu \(\Omega \) là tập hợp gồm 4 000 bệnh nhân thử nghiệm nên \(n\left( \Omega \right) = 4000\)
a) Gọi A là biến cố: “Người đó uống thuốc M”, B là biến cố “Người đó khỏi bệnh”
Khi đó biến cố AB là: “Người đó uống thuốc M và khỏi bệnh”
Ta có: \(1600 + 1200 = 2800\) người khỏi bệnh nên \(n\left( B \right) = 2800\). Do đó, \(P\left( B \right) = \frac{{2800}}{{4000}}\)
Trong số những người khỏi bệnh, có 1 600 người uống thuốc M nên \(n\left( {AB} \right) = 1\;600\)
Do đó, \(P\left( {AB} \right) = \frac{{1600}}{{4000}}\). Vậy \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{1600}}{{2800}} = \frac{4}{7}\)
b) Gọi A là biến cố: “Người đó uống thuốc N”, B là biến cố “Người đó không khỏi bệnh”.
Khi đó biến cố AB là: “Người đó uống thuốc N và không khỏi bệnh”
Ta có: \(800 + 400 = 1200\) người không khỏi bệnh nên \(n\left( B \right) = 1200\). Do đó, \(P\left( B \right) = \frac{{1200}}{{4000}}\)
Trong số những người không khỏi bệnh, có 400 người uống thuốc N nên \(n\left( {AB} \right) = 400\)
Do đó, \(P\left( {AB} \right) = \frac{{400}}{{4000}}\). Vậy \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{400}}{{1200}} = \frac{1}{3}\)
Mục 1 của chương trình Toán 12 tập 2 Kết nối tri thức thường tập trung vào một chủ đề quan trọng, thường là về một loại hàm số, một phương pháp giải toán cụ thể, hoặc một ứng dụng của toán học trong thực tế. Việc nắm vững kiến thức và kỹ năng trong mục này là nền tảng để giải quyết các bài toán phức tạp hơn trong các chương tiếp theo.
Để giúp các em hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 1 trang 65, 66, 67, chúng ta sẽ đi vào phân tích chi tiết từng bài tập:
Bài tập này thường yêu cầu các em vận dụng kiến thức về... (nêu cụ thể kiến thức liên quan đến bài tập). Để giải bài tập này, các em cần thực hiện các bước sau:
Ví dụ minh họa: ... (giải chi tiết bài tập)
Bài tập này tập trung vào việc... (nêu cụ thể kiến thức liên quan đến bài tập). Lưu ý khi giải bài tập này là... (nêu các lưu ý quan trọng).
Lời giải:
...
Bài tập này là một bài toán ứng dụng thực tế, yêu cầu các em... (nêu yêu cầu của bài tập). Để giải quyết bài toán này, các em cần:
...
Ngoài các bài tập cụ thể trong SGK, các em cũng có thể gặp các dạng bài tập tương tự trong các đề thi và bài kiểm tra. Dưới đây là một số dạng bài tập thường gặp:
Để học tập và ôn thi môn Toán 12 hiệu quả, các em nên:
Ngoài SGK, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, các em sẽ hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 1 trang 65, 66, 67 SGK Toán 12 tập 2 Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!