Bài tập 1.4 trang 13 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Kết nối tri thức, tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về hàm số bậc hai, điều kiện xác định, tập giá trị, và các tính chất của hàm số để giải quyết.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 1.4 trang 13 SGK Toán 12 tập 1 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Xét chiều biến thiên của các hàm số sau: a) (y = sqrt {4 - {x^2}} ); b) (y = frac{x}{{{x^2} + 1}}).
Đề bài
Xét chiều biến thiên của các hàm số sau:a) \(y = \sqrt {4 - {x^2}} \);b) \(y = \frac{x}{{{x^2} + 1}}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về các bước để xét tính đơn điệu để xét chiều biến thiên của hàm số: Các bước để xét tính đơn điệu của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm \(f'\left( x \right)\). Tìm các điểm \({x_i}\left( {i = 1,2,...} \right)\) mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
3. Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên của hàm số.
4. Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết
a) Tập xác định: \(D = \left[ { - 2;2} \right]\).
Ta có: \(y' = \frac{{\left( {4 - {x^2}} \right)'}}{{2\sqrt {4 - {x^2}} }} = \frac{{ - x}}{{\sqrt {4 - {x^2}} }},y' = 0 \Leftrightarrow x = 0\left( {tm} \right)\)
Lập bảng biến thiên của hàm số:
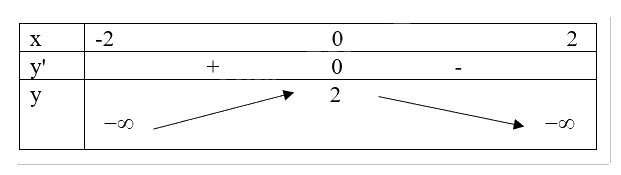
Hàm số \(y = \sqrt {4 - {x^2}} \) đồng biến trên khoảng \(\left( { - 2;0} \right)\).
Hàm số \(y = \sqrt {4 - {x^2}} \) nghịch biến trên khoảng \(\left( {0;2} \right)\).
b) Tập xác định: \(D = \mathbb{R}\).
Ta có:
\(y' = \frac{{x'({x^2} + 1) - x({x^2} + 1)'}}{{{{({x^2} + 1)}^2}}} = \frac{{{x^2} + 1 - 2{x^2}}}{{{{({x^2} + 1)}^2}}} = \frac{{ - {x^2} + 1}}{{{{({x^2} + 1)}^2}}}\).
\(y' = 0 \Leftrightarrow \frac{{ - {x^2} + 1}}{{{{({x^2} + 1)}^2}}} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = - 1}\end{array}} \right.\).
Lập bảng biến thiên của hàm số:
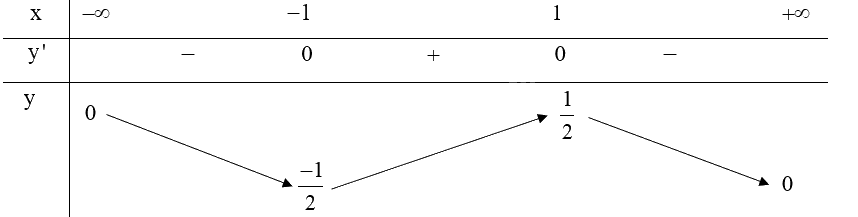
Hàm số \(y = \frac{x}{{{x^2} + 1}}\) nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\), \(\left( {1; + \infty } \right)\).
Hàm số \(y = \frac{x}{{{x^2} + 1}}\) đồng biến trên khoảng \(\left( { - 1;1} \right)\).
Bài tập 1.4 trang 13 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai và ứng dụng của nó. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản như:
Nội dung bài tập 1.4: Bài tập thường yêu cầu xác định các yếu tố của hàm số bậc hai (a, b, c), tìm tọa độ đỉnh, trục đối xứng, tập giá trị, vẽ đồ thị hàm số, hoặc giải các bài toán liên quan đến ứng dụng của hàm số bậc hai trong thực tế.
Bài toán: Cho hàm số y = x2 - 4x + 3. Tìm tọa độ đỉnh và vẽ đồ thị hàm số.
Giải:
Lưu ý: Khi vẽ đồ thị hàm số bậc hai, cần chú ý đến dấu của hệ số a để xác định hướng mở của parabol (hướng lên trên nếu a > 0, hướng xuống dưới nếu a < 0).
Lời khuyên: Để học tốt bài tập 1.4 trang 13 SGK Toán 12 tập 1 - Kết nối tri thức, các em cần nắm vững lý thuyết, làm nhiều bài tập, và tham khảo các tài liệu học tập khác. Giaitoan.edu.vn hy vọng sẽ là một nguồn tài liệu hữu ích giúp các em học Toán 12 hiệu quả.
Bài tập 1.4 trang 13 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hàm số bậc hai và ứng dụng của nó. Bằng cách nắm vững các khái niệm cơ bản và luyện tập thường xuyên, các em sẽ tự tin giải quyết các bài toán liên quan đến hàm số bậc hai.