Bài tập 1.3 trang 13 SGK Toán 12 tập 1 thuộc chương trình Kết nối tri thức là một phần quan trọng trong quá trình ôn luyện và củng cố kiến thức về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng các định nghĩa và tính chất của giới hạn để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 1.3 trang 13 SGK Toán 12 tập 1 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Tìm các khoảng đơn điệu của các hàm số sau: a) \(y = \frac{{2x - 1}}{{x + 2}}\); b) \(y = \frac{{{x^2} + x + 4}}{{x - 3}}\).
Đề bài
Tìm các khoảng đơn điệu của các hàm số sau:
a) \(y = \frac{{2x - 1}}{{x + 2}}\);
b) \(y = \frac{{{x^2} + x + 4}}{{x - 3}}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về các bước để xét tính đơn điệu để xét khoảng đồng biến của hàm số: Các bước để xét tính đơn điệu của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm \(f'\left( x \right)\). Tìm các điểm \({x_i}\left( {i = 1,2,...} \right)\) mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
3. Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên của hàm số.
4. Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết
a) Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có: \(y' = \frac{{2\left( {x + 2} \right) - \left( {2x - 1} \right)}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{2x + 4 - 2x + 1}}{{{{\left( {x + 2} \right)}^2}}} = \frac{5}{{\left( {x + 2} \right)}} > 0\;\forall x \ne - 2\)
Do đó, hàm số \(y = \frac{{2x - 1}}{{x + 2}}\) đồng biến trên \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 3 \right\}\).
Ta có: \(y' = \frac{{\left( {{x^2} + x + 4} \right)'\left( {x - 3} \right) - \left( {{x^2} + x + 4} \right)\left( {x - 3} \right)'}}{{{{\left( {x - 3} \right)}^2}}} = \frac{{\left( {2x + 1} \right)\left( {x - 3} \right) - {x^2} - x - 4}}{{{{\left( {x - 3} \right)}^2}}} = \frac{{{x^2} - 6x - 7}}{{{{\left( {x - 3} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow \frac{{{x^2} - 6x - 7}}{{{{\left( {x - 3} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 7\\x = - 1\end{array} \right.\) (thỏa mãn)
Lập bảng biến thiên của hàm số:
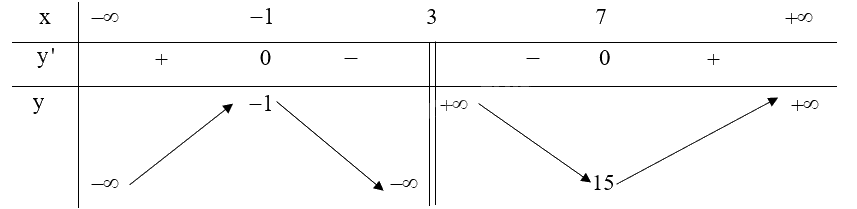
Từ bảng biến thiên ta thấy:
Hàm số \(y = \frac{{{x^2} + x + 4}}{{x - 3}}\) nghịch biến trên khoảng \(\left( { - 1;3} \right)\) và \(\left( {3;7} \right)\).
Hàm số \(y = \frac{{{x^2} + x + 4}}{{x - 3}}\) đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {7; + \infty } \right)\).
Bài tập 1.3 trang 13 SGK Toán 12 tập 1 - Kết nối tri thức tập trung vào việc tính giới hạn của hàm số tại một điểm. Để giải quyết bài tập này, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, bao gồm định nghĩa giới hạn, các tính chất của giới hạn, và các phương pháp tính giới hạn.
Bài tập 1.3 thường bao gồm các dạng bài sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập 1.3 trang 13 SGK Toán 12 tập 1 - Kết nối tri thức, chúng ta sẽ đi vào giải chi tiết từng câu hỏi.
Để tính giới hạn này, ta có thể thay trực tiếp x = 2 vào biểu thức:
limx→2 (x2 - 4x + 3) = 22 - 4*2 + 3 = 4 - 8 + 3 = -1
Ta có thể phân tích tử thức thành nhân tử:
x3 - 1 = (x - 1)(x2 + x + 1)
Do đó:
limx→1 (x3 - 1) / (x - 1) = limx→1 (x2 + x + 1) = 12 + 1 + 1 = 3
Đây là một giới hạn lượng giác cơ bản:
limx→0 sin(x) / x = 1
Ngoài việc áp dụng trực tiếp các định nghĩa và tính chất, học sinh có thể sử dụng các phương pháp sau để giải bài tập giới hạn:
Khi giải bài tập giới hạn, học sinh cần lưu ý những điều sau:
Bài tập 1.3 trang 13 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn của hàm số. Bằng cách nắm vững các khái niệm cơ bản, các phương pháp giải bài tập, và các lưu ý khi giải bài tập, học sinh có thể tự tin giải quyết các bài tập giới hạn một cách hiệu quả.