Bài tập 5.24 trang 53 SGK Toán 12 tập 2 thuộc chương trình học Toán 12 Kết nối tri thức. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến tính đơn điệu của hàm số, cực trị của hàm số, hoặc các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 5.24, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
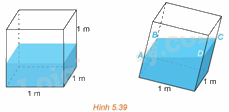
(H.5.39) Trong một bể hình lập phương cạnh 1m có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành ABCD và khoảng cách từ các điểm A, B, C đến đáy bể tương ứng là 40cm, 44cm, 48cm. a) Khoảng cách từ điểm D đến đáy bể bằng bao nhiêu centimét? (Tính gần đúng, lấy giá trị nguyên.) b) Đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ?
Đề bài
(H.5.39) Trong một bể hình lập phương cạnh 1m có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành ABCD và khoảng cách từ các điểm A, B, C đến đáy bể tương ứng là 40cm, 44cm, 48cm.
a) Khoảng cách từ điểm D đến đáy bể bằng bao nhiêu centimét? (Tính gần đúng, lấy giá trị nguyên.)
b) Đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ?
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)) được tính theo công thức:
\(\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\)
Lời giải chi tiết
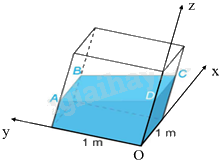
a) Chọn hệ trục tọa độ Oxyz như hình vẽ.
Khi đó, \(A\left( {0;1;0,4} \right),B\left( {1;1;0,44} \right),C\left( {1;0;0,48} \right),D\left( {0;0;z} \right)\)
Suy ra: \(\overrightarrow {AB} \left( {1;0;0,04} \right),\overrightarrow {DC} \left( {1;0,0,48 - z} \right)\)
Vì ABCD là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \Rightarrow 0,48 - z = 0,04 \Rightarrow z = 0,44\)
Do đó, \(D\left( {0;0;0,44} \right)\). Vậy khoảng cách từ D đến đáy bể bằng 44cm.
b) Đặt tên các điểm như hình vẽ. Kẻ AA’ vuông góc với Oz tại A’.
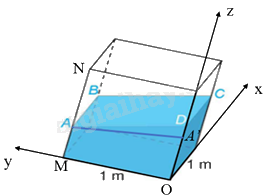
Mặt phẳng (Oxz) nhận \(\overrightarrow j \left( {0;1;0} \right)\) làm vectơ pháp tuyến nên phương trình mặt phẳng (Oxz) là: \(y = 0\).
Ta có: \(AA' = d\left( {A,\left( {Oxz} \right)} \right) = \frac{{\left| 1 \right|}}{{\sqrt 1 }} = 1\), \(AD = \sqrt {{1^2} + 0,{{04}^2}} = \frac{{\sqrt {626} }}{{25}}\)
Tam giác ADA’ vuông tại A’ nên \(\cos \left( {AA',DA} \right) = \frac{{AA'}}{{AD}} = \frac{1}{{\frac{{\sqrt {626} }}{{25}}}} \Rightarrow \left( {AA',AD} \right) \approx 2,{3^o}\)
Vậy đáy bể nghiêng mới mặt nằm ngang một góc khoảng \(2,{3^o}\).
Bài tập 5.24 SGK Toán 12 tập 2 Kết nối tri thức là một bài toán quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và định lý liên quan, cũng như kỹ năng biến đổi đại số và giải phương trình.
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu của bài toán. Xác định rõ hàm số cần khảo sát, các điều kiện cho trước và những gì cần tìm. Trong bài tập 5.24, yêu cầu thường là tìm khoảng đơn điệu, cực trị hoặc giải phương trình, bất phương trình liên quan đến hàm số.
Đạo hàm của hàm số đóng vai trò quan trọng trong việc giải bài tập này. Học sinh cần tính đạo hàm cấp một và đạo hàm cấp hai của hàm số. Sau đó, sử dụng đạo hàm cấp một để xác định khoảng đơn điệu của hàm số. Đạo hàm cấp hai giúp xác định điểm uốn và tính chất lồi lõm của đồ thị hàm số.
Để tìm khoảng đơn điệu của hàm số, học sinh cần giải bất phương trình f'(x) > 0 và f'(x) < 0. Nghiệm của các bất phương trình này sẽ xác định khoảng tăng và khoảng giảm của hàm số. Lưu ý rằng, cần xét dấu của đạo hàm trên từng khoảng xác định của hàm số.
Cực trị của hàm số là các điểm mà tại đó đạo hàm cấp một bằng 0 hoặc không tồn tại. Để xác định cực đại hoặc cực tiểu, học sinh cần xét dấu của đạo hàm cấp một xung quanh các điểm nghi ngờ. Nếu đạo hàm đổi dấu từ dương sang âm, đó là điểm cực đại. Nếu đạo hàm đổi dấu từ âm sang dương, đó là điểm cực tiểu.
Trong một số trường hợp, bài tập 5.24 có thể yêu cầu giải phương trình hoặc bất phương trình liên quan đến hàm số. Để giải quyết các bài toán này, học sinh cần sử dụng các kỹ năng biến đổi đại số, giải phương trình bậc hai, bậc ba hoặc sử dụng các phương pháp đặc biệt như phương pháp đổi biến.
Giả sử hàm số cần khảo sát là f(x) = x3 - 3x2 + 2. Ta thực hiện các bước sau:
Khi giải bài tập 5.24, học sinh cần chú ý các điểm sau:
Kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số có nhiều ứng dụng trong thực tế, như:
Bài tập 5.24 trang 53 SGK Toán 12 tập 2 Kết nối tri thức là một bài toán quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Bằng cách nắm vững các khái niệm và định lý liên quan, rèn luyện kỹ năng giải toán và áp dụng các phương pháp phù hợp, học sinh có thể giải quyết bài tập này một cách hiệu quả và đạt kết quả tốt trong kỳ thi.