Bài tập 1.24 trang 32 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 1.24 trang 32 SGK Toán 12 tập 1, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Một cốc chứa 30ml dung dịch KOH (potassium hydroxide) với nồng độ 100mg/ml. Một bình chứa dung dịch KOH khác chứa nồng độ 8mg/ml được trộn vào cốc. a) Tính nồng độ KOH trong cốc sau khi trộn x (ml) từ bình chứa, kí hiệu là C(x). b) Coi hàm C(x) là hàm số xác định với \(x \ge 0\). Khảo sát sự biến thiên và vẽ đồ thị của hàm số này. c) Giải thích tại sao nồng độ KOH trong cốc giảm theo x nhưng luôn lớn hơn 8mg/ml.
Đề bài
Một cốc chứa 30ml dung dịch KOH (potassium hydroxide) với nồng độ 100mg/ml. Một bình chứa dung dịch KOH khác chứa nồng độ 8mg/ml được trộn vào cốc.
a) Tính nồng độ KOH trong cốc sau khi trộn x (ml) từ bình chứa, kí hiệu là C(x).
b) Coi hàm C(x) là hàm số xác định với \(x \ge 0\). Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.
c) Giải thích tại sao nồng độ KOH trong cốc giảm theo x nhưng luôn lớn hơn 8mg/ml.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về sơ đồ khảo sát hàm số phân thức để khảo sát và vẽ đồ thị hàm số:
Sơ đồ khảo sát hàm số phân thức
1. Tìm tập xác định của hàm số.
2. Khảo sát sự biến thiên của hàm số:
+ Tính đạo hàm y’. Tìm các điểm tại đó y’ bằng 0 hoặc đạo hàm không tồn tại.
+ Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số.
+ Tìm cực trị của hàm số.
+ Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số.
+ Lập bảng biến thiên của hàm số.
3. Vẽ đồ thị của hàm số dựa vào bảng biến thiên.
Lời giải chi tiết
a) Khối lượng dung dịch trong cốc sau khi trộn x(ml) KOH từ bình chứa là: \(m = 30.100 + 8x = 8x + 3\;000\left( {mg} \right)\)
Thể tích dung dịch trong cốc sau khi trộn x(ml) KOH từ bình chứa là: \(V = 30 + x\left( {ml} \right)\)
Nồng độ KOH trong cốc sau khi trộn x (ml) từ bình chứa là:
\(C\left( x \right) = \frac{m}{V} = \frac{{8x + 3000}}{{30 + x}}\left( {mg/ml} \right)\)
b) Khảo sát hàm số \(y = C\left( x \right) = \frac{{8x + 3000}}{{x + 30}}\) với \(x \ge 0\).
1. Tập xác định của hàm số: \(\left[ {0; + \infty } \right)\)
2. Sự biến thiên:
\(C'\left( x \right) = \frac{{ - 2760}}{{{{\left( {x + 30} \right)}^2}}} < 0\forall x \ge 0\)
Hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).
Hàm số không có cực trị.
\(\mathop {\lim }\limits_{x \to + \infty } C\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{8x + 3000}}{{x + 30}} = 8\).
Do đó, đồ thị hàm số \(y = C\left( x \right) = \frac{{8x + 3000}}{{x + 30}}\) nhận đường thẳng \(y = 8\) làm tiệm cận ngang (phần bên phải trục Oy)
Bảng biến thiên:

3. Đồ thị: Giao điểm của đồ thị hàm số với trục tung là (0;100).
Đồ thị hàm số \(y = C\left( x \right) = \frac{{8x + 3000}}{{x + 30}}\) đi qua các điểm (200; 20); \(\left( {120;\frac{{132}}{5}} \right)\).
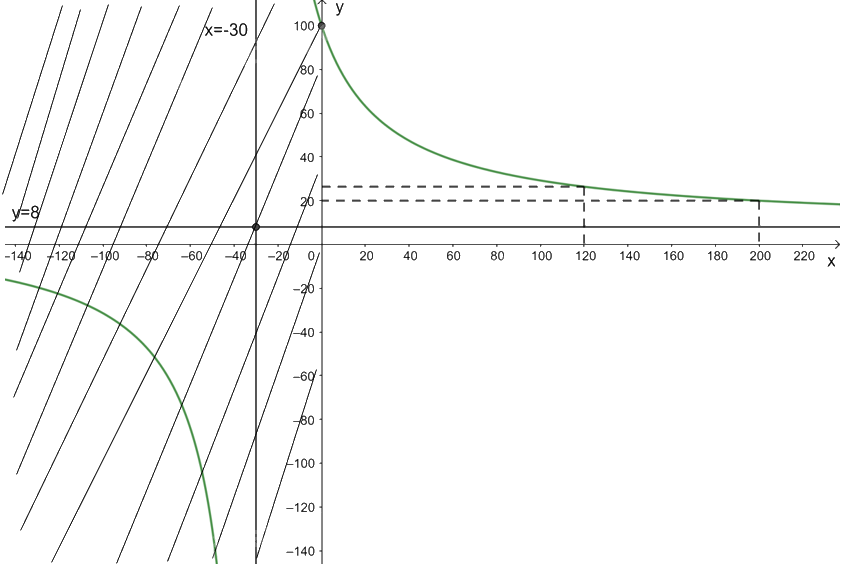
Đồ thị của hàm số \(y = C\left( x \right) = \frac{{8x + 3000}}{{x + 30}}\) với \(x \ge 0\) là phần nét màu xanh không bị gạch chéo.
c) Vì \(C'\left( x \right) = \frac{{ - 2760}}{{{{\left( {x + 30} \right)}^2}}} < 0\forall x \ge 0\) và \(\mathop {\lim }\limits_{x \to + \infty } C\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{8x + 3000}}{{x + 30}} = 8\) nên nồng độ KOH trong cốc giảm theo x nhưng luôn lớn hơn 8mg/ml
Bài tập 1.24 trang 32 SGK Toán 12 tập 1 - Kết nối tri thức là một bài toán quan trọng trong chương trình học Toán 12, tập trung vào việc ứng dụng đạo hàm để giải quyết các bài toán thực tế liên quan đến tốc độ thay đổi của một đại lượng. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về đạo hàm, quy tắc tính đạo hàm và các ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu của bài toán. Xác định rõ các đại lượng đã cho, các mối quan hệ giữa chúng và mục tiêu cần tìm. Trong bài tập 1.24, thường yêu cầu tìm đạo hàm của một hàm số, xác định các điểm cực trị hoặc giải một phương trình liên quan đến đạo hàm.
Để tính đạo hàm của một hàm số, học sinh cần áp dụng các quy tắc tính đạo hàm đã học, bao gồm:
Việc nắm vững và áp dụng thành thạo các quy tắc này là yếu tố then chốt để giải quyết bài tập một cách nhanh chóng và chính xác.
Để tìm cực trị của một hàm số, học sinh cần thực hiện các bước sau:
Việc tìm cực trị của hàm số có ứng dụng rộng rãi trong nhiều lĩnh vực, như tối ưu hóa sản xuất, tìm giá trị lớn nhất và nhỏ nhất của một đại lượng.
Trong một số bài tập, yêu cầu đặt ra là giải một phương trình liên quan đến đạo hàm. Để giải quyết bài toán này, học sinh cần sử dụng các kỹ năng giải phương trình đã học, kết hợp với các kiến thức về đạo hàm để biến đổi phương trình về dạng đơn giản hơn và tìm ra nghiệm.
(Nội dung ví dụ giải chi tiết bài tập 1.24 sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, giải thích rõ ràng và kết luận chính xác. Ví dụ này sẽ bao gồm các phép tính đạo hàm, tìm cực trị, hoặc giải phương trình liên quan đến đạo hàm, tùy thuộc vào yêu cầu của bài tập.)
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững phương pháp giải và tự tin giải quyết các bài toán khó hơn.
Bài tập 1.24 trang 32 SGK Toán 12 tập 1 - Kết nối tri thức là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng ứng dụng đạo hàm để giải quyết các bài toán thực tế. Bằng cách nắm vững các khái niệm cơ bản, quy tắc tính đạo hàm và phương pháp giải bài tập, học sinh có thể tự tin chinh phục bài toán này và đạt kết quả tốt trong môn Toán 12.
| Khái niệm | Giải thích |
|---|---|
| Đạo hàm | Tốc độ thay đổi tức thời của một hàm số tại một điểm. |
| Cực trị | Điểm mà hàm số đạt giá trị lớn nhất hoặc nhỏ nhất trong một khoảng nào đó. |
| Đạo hàm bậc nhất | Đạo hàm của hàm số. |
| Đạo hàm bậc hai | Đạo hàm của đạo hàm bậc nhất. |