Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 3 trang 46, 47, 48 sách giáo khoa Toán 12 tập 2 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt nhất trong môn Toán.
VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG
Trả lời câu hỏi Luyện tập 8 trang 46 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, chứng minh rằng hai đường thẳng sau song song với nhau:
\({\Delta _1}:\frac{{x - 3}}{1} = \frac{y}{{ - 2}} = \frac{{z - 1}}{3}\) và \({\Delta _2}:\frac{{x - 1}}{1} = \frac{{y - 2}}{{ - 2}} = \frac{z}{3}\).
Phương pháp giải:
Sử dụng kiến thức về vị trí tương đối của hai đường thẳng để chứng minh: Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}\left( {{x_1};{y_1};{z_1}} \right),{A_2}\left( {{x_2};{y_2};{z_2}} \right)\) và tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\). Khi đó, \({\Delta _1}//{\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1}\not \in {\Delta _2}\)
Lời giải chi tiết:
Đường thẳng \({\Delta _1}\) đi qua điểm \({A_1}\left( {3;0;1} \right)\) và có một vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {1; - 2;3} \right)\).
Đường thẳng \({\Delta _2}\) có một vectơ chỉ phương \(\overrightarrow {{u_2}} = \left( {1; - 2;3} \right)\).
Vì \(\overrightarrow {{u_1}} = \overrightarrow {{u_2}} \) nên \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \).
Lại có: \(\frac{{3 - 1}}{1} \ne \frac{{0 - 2}}{{ - 2}} \ne \frac{1}{3}\) nên điểm \({A_1}\left( {3;0;1} \right)\) không thuộc đường thẳng \({\Delta _2}\).
Do đó, hai đường thẳng \({\Delta _1},{\Delta _2}\) song song với nhau.
Trả lời câu hỏi Luyện tập 9 trang 47 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1}:\frac{{x - 1}}{1} = \frac{{y + 2}}{1} = \frac{{z - 3}}{4}\) và \({\Delta _2}:\frac{{x + 1}}{1} = \frac{{y + 1}}{1} = \frac{z}{4}\). Chứng minh rằng:
a) Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) song song với nhau;
b) Đường thẳng \({\Delta _1}\) và trục Ox chéo nhau;
c) Đường thẳng \({\Delta _2}\) trùng với đường thẳng \({\Delta _3}:\frac{{x + 2}}{1} = \frac{{y + 2}}{1} = \frac{{z + 4}}{4}\);
d) Đường thẳng \({\Delta _2}\) cắt trục Oz.
Phương pháp giải:
Sử dụng kiến thức về vị trí tương đối của hai đường thẳng để chứng minh: Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}\left( {{x_1};{y_1};{z_1}} \right),{A_2}\left( {{x_2};{y_2};{z_2}} \right)\) và tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\). Khi đó:
\({\Delta _1}//{\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1}\not \in {\Delta _2}\)
\({\Delta _1} \equiv {\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1} \in {\Delta _2}\)
\({\Delta _1}\) và \({\Delta _2}\) chéo nhau \( \Leftrightarrow \overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\)
\({\Delta _1}\) và \({\Delta _2}\) cắt nhau \( \Leftrightarrow \left\{ \begin{array}{l}\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \\\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\end{array} \right.\)
Lời giải chi tiết:
Đường thẳng \({\Delta _1}\) đi qua điểm \({A_1}\left( {1; - 2;3} \right)\) và có một vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {1;1;4} \right)\).
Đường thẳng \({\Delta _2}\) đi qua điểm \({A_2}\left( { - 1; - 1;0} \right)\) và có một vectơ chỉ phương \(\overrightarrow {{u_2}} = \left( {1;1;4} \right)\).
a) Vì \(\overrightarrow {{u_1}} = \overrightarrow {{u_2}} \) nên \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \).
Lại có: \(\frac{{1 + 1}}{1} \ne \frac{{ - 2 + 1}}{1}\) nên điểm \({A_1}\left( {1; - 2;3} \right)\) không thuộc đường thẳng \({\Delta _2}\).
Do đó, hai đường thẳng \({\Delta _1},{\Delta _2}\) song song với nhau.
b) Trục Ox có một vectơ chỉ phương \(\overrightarrow i = \left( {1;0;0} \right)\) và đi qua điểm O(0;0;0).
Ta có: \(\left[ {\overrightarrow {{u_1}} ;\overrightarrow i } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&4\\0&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}4&1\\0&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}1&1\\1&0\end{array}} \right|} \right) = \left( {0;4; - 1} \right)\), \(\overrightarrow {{A_1}O} \left( { - 1;2; - 3} \right)\)
Vì \(\overrightarrow {{A_1}O} .\left[ {\overrightarrow {{u_1}} ;\overrightarrow i } \right] = - 1.0 + 2.4 - 3.\left( { - 1} \right) = 11 \ne 0\) nên \({\Delta _1}\) và Ox chéo nhau.
c) Đường thẳng \({\Delta _3}\) có một vectơ chỉ phương \(\overrightarrow {{u_3}} = \left( {1;1;4} \right)\).
Vì \(\overrightarrow {{u_3}} = \overrightarrow {{u_2}} \) nên \(\overrightarrow {{u_3}} \) cùng phương với \(\overrightarrow {{u_2}} \).
Lại có: \(\frac{{ - 1 + 2}}{1} = \frac{{ - 1 + 2}}{1} = \frac{{0 + 4}}{4}\) nên điểm \({A_2}\left( { - 1; - 1;0} \right)\) thuộc đường thẳng \({\Delta _3}\).
Do đó, đường thẳng \({\Delta _2}\) trùng với đường thẳng \({\Delta _3}\).
d) Trục Oz có một vectơ chỉ phương \(\overrightarrow k = \left( {0;0;1} \right)\) và đi qua điểm O(0;0;0)
Ta có: \(\left[ {\overrightarrow {{u_2}} ,\overrightarrow k } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&4\\0&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}4&1\\1&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}1&1\\0&0\end{array}} \right|} \right) = \left( {1; - 1;0} \right)\), \(\overrightarrow {{A_2}O} \left( {1;1;0} \right)\)
Vì \(\overrightarrow {{A_2}O} .\left[ {\overrightarrow {{u_2}} ,\overrightarrow k } \right] = 1.1 - 1.1 - 0.0 = 0\) và \(\left[ {\overrightarrow {{u_2}} ,\overrightarrow k } \right] = \left( {1; - 1;0} \right) \ne \overrightarrow 0 \) nên \({\Delta _2}\) cắt trục Oz.
Trả lời câu hỏi Luyện tập 10 trang 48 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, xét vị trí tương đối giữa hai đường thẳng: \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + t\\z = 1 - t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = s\\y = 1 + 2s\\z = 3s\end{array} \right.\).
Phương pháp giải:
Sử dụng kiến thức về vị trí tương đối của hai đường thẳng để tìm vị trí tương đối của \({\Delta _1}\) và \({\Delta _2}\): Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\) và có phương trình tham số: \({\Delta _1}:\left\{ \begin{array}{l}x = {x_1} + {a_1}t\\y = {y_1} + {b_1}t\\z = {z_1} + {c_1}t\end{array} \right.\) \({\Delta _2}:\left\{ \begin{array}{l}x = {x_2} + {a_2}s\\y = {y_2} + {b_2}s\\z = {z_2} + {c_2}s\end{array} \right.\). Xét hệ phương trình hai ẩn t, s: \(\left\{ \begin{array}{l}{x_1} + {a_1}t = {x_2} + {a_2}s\\{y_1} + {b_1}t = {y_2} + {b_2}s\\{z_1} + {c_1}t = {z_2} + {c_2}s\end{array} \right.\left( * \right)\)
\({\Delta _1}//{\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và hệ (*) vô nghiệm.
\({\Delta _1} \equiv {\Delta _2} \Leftrightarrow \) Hệ (*) có vô số nghiệm.
\({\Delta _1}\) và \({\Delta _2}\) chéo nhau \( \Leftrightarrow \)\(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương và hệ (*) vô nghiệm.
\({\Delta _1}\) và \({\Delta _2}\) cắt nhau \( \Leftrightarrow \) Hệ (*) có nghiệm duy nhất
Lời giải chi tiết:
\({\Delta _1}\) và \({\Delta _2}\) có vectơ chỉ phương lần lượt là \(\overrightarrow {{u_1}} = \left( {2;1; - 1} \right)\) và \(\overrightarrow {{u_2}} = \left( {1;2;3} \right)\)
Vì \(\frac{2}{1} \ne \frac{1}{2}\) nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương. Do đó, \({\Delta _1}\) và \({\Delta _2}\) cắt nhau hoặc chéo nhau.
Xét hệ phương trình: \(\left\{ \begin{array}{l}1 + 2t = s\\3 + t = 1 + 2s\\1 - t = 3s\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}s - 2t = 1\;\left( 1 \right)\\2s - t = 2\;\left( 2 \right)\\3s + t = 1\;\left( 3 \right)\end{array} \right.\)
Từ (1) và (2) ta có: \(s = 1;t = 0\), thay vào (3) ta thấy không thỏa mãn phương trình.
Do đó, hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) chéo nhau.
Trả lời câu hỏi Hoạt động 6 trang 46 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}\left( {{x_1};{y_1};{z_1}} \right),{A_2}\left( {{x_2};{y_2};{z_2}} \right)\) và tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\). (H.5.29).
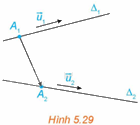
a) Tìm điều kiện đối với \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) để \({\Delta _1}\) và \({\Delta _2}\) song song hoặc trùng nhau.
b) Giả sử \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \) và \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\) thì \({\Delta _1}\) và \({\Delta _2}\) có cắt nhau hay không?
c) Giả sử \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\) thì \({\Delta _1}\) và \({\Delta _2}\) có chéo nhau hay không?
Phương pháp giải:
Sử dụng kiến thức về giá của vectơ trong không gian để tìm chứng minh: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ.
Lời giải chi tiết:
a) Để \({\Delta _1}\) và \({\Delta _2}\) song song hoặc trùng nhau thì giá của hai vectơ \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) song song hoặc trùng nhau. Suy ra, \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) cùng phương.
b) Vì \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \) mà \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\) nên \(\overrightarrow {{A_1}{A_2}} = \overrightarrow 0 \), suy ra \({A_1}\) trùng \({A_2}\). Do đó, \({\Delta _1}\) và \({\Delta _2}\) cắt nhau.
c) Vì \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\) nên \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \) và \(\overrightarrow {{A_1}{A_2}} \ne \overrightarrow 0 \) nên \({\Delta _1}\) và \({\Delta _2}\) chéo nhau.
Trả lời câu hỏi Vận dụng 3 trang 48 SGK Toán 12 Kết nối tri thức
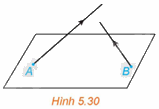
(H.5.30) Trong không gian Oxyz, có hai vật thể lần lượt xuất phát từ A(1; 2; 0) và B(3; 5; 0) với vận tốc không đổi tương ứng là \(\overrightarrow {{v_1}} = \left( {2;1;3} \right),\overrightarrow {{v_2}} = \left( {1;2;1} \right)\). Hỏi trong quá trình chuyển động, hai vật thể trên có va chạm vào nhau hay không?
Phương pháp giải:
Sử dụng kiến thức về vị trí tương đối của hai đường thẳng để giải: Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}\left( {{x_1};{y_1};{z_1}} \right),{A_2}\left( {{x_2};{y_2};{z_2}} \right)\) và tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\). Khi đó:
\({\Delta _1}//{\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1}\not \in {\Delta _2}\).
\({\Delta _1} \equiv {\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1} \in {\Delta _2}\).
\({\Delta _1}\) và \({\Delta _2}\) chéo nhau \( \Leftrightarrow \overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\).
\({\Delta _1}\) và \({\Delta _2}\) cắt nhau \( \Leftrightarrow \left\{ \begin{array}{l}\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \\\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\end{array} \right.\) .
Lời giải chi tiết:
Gọi d là đường thẳng đi qua A và có vectơ chỉ phương là \(\overrightarrow {{v_1}} =\left( {2;1;3} \right)\).
Gọi d’ là đường thẳng đi qua B và có vectơ chỉ phương là \(\overrightarrow {{v_2}} =\left( {1;2;1} \right)\).
Vì \(\frac{2}{1} \ne \frac{1}{2}\) nên hai vectơ \(\overrightarrow {{v_1}} \) và \(\overrightarrow {{v_2}} \) không cùng phương.
Ta có: \(\left[ {\overrightarrow {{v_1}} ;\overrightarrow {{v_2}} } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&3\\2&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}3&2\\1&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}2&1\\1&2\end{array}} \right|} \right) = \left( { - 5;1;3} \right) \ne \overrightarrow 0 \), \(\overrightarrow {AB} \left( {2;3;0} \right)\).
Vì \(\overrightarrow {AB} .\left[ {\overrightarrow {{v_1}} ;\overrightarrow {{v_2}} } \right] = \left( { - 5} \right).2 + 1.3 + 3.0 = - 7 \ne 0\) nên d và d’ chéo nhau.
Do đó, hai vật trên không va chạm vào nhau.
Trả lời câu hỏi Hoạt động 6 trang 46 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}\left( {{x_1};{y_1};{z_1}} \right),{A_2}\left( {{x_2};{y_2};{z_2}} \right)\) và tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\). (H.5.29).
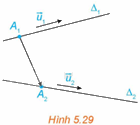
a) Tìm điều kiện đối với \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) để \({\Delta _1}\) và \({\Delta _2}\) song song hoặc trùng nhau.
b) Giả sử \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \) và \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\) thì \({\Delta _1}\) và \({\Delta _2}\) có cắt nhau hay không?
c) Giả sử \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\) thì \({\Delta _1}\) và \({\Delta _2}\) có chéo nhau hay không?
Phương pháp giải:
Sử dụng kiến thức về giá của vectơ trong không gian để tìm chứng minh: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ.
Lời giải chi tiết:
a) Để \({\Delta _1}\) và \({\Delta _2}\) song song hoặc trùng nhau thì giá của hai vectơ \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) song song hoặc trùng nhau. Suy ra, \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) cùng phương.
b) Vì \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \) mà \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\) nên \(\overrightarrow {{A_1}{A_2}} = \overrightarrow 0 \), suy ra \({A_1}\) trùng \({A_2}\). Do đó, \({\Delta _1}\) và \({\Delta _2}\) cắt nhau.
c) Vì \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\) nên \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \) và \(\overrightarrow {{A_1}{A_2}} \ne \overrightarrow 0 \) nên \({\Delta _1}\) và \({\Delta _2}\) chéo nhau.
Trả lời câu hỏi Luyện tập 8 trang 46 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, chứng minh rằng hai đường thẳng sau song song với nhau:
\({\Delta _1}:\frac{{x - 3}}{1} = \frac{y}{{ - 2}} = \frac{{z - 1}}{3}\) và \({\Delta _2}:\frac{{x - 1}}{1} = \frac{{y - 2}}{{ - 2}} = \frac{z}{3}\).
Phương pháp giải:
Sử dụng kiến thức về vị trí tương đối của hai đường thẳng để chứng minh: Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}\left( {{x_1};{y_1};{z_1}} \right),{A_2}\left( {{x_2};{y_2};{z_2}} \right)\) và tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\). Khi đó, \({\Delta _1}//{\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1}\not \in {\Delta _2}\)
Lời giải chi tiết:
Đường thẳng \({\Delta _1}\) đi qua điểm \({A_1}\left( {3;0;1} \right)\) và có một vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {1; - 2;3} \right)\).
Đường thẳng \({\Delta _2}\) có một vectơ chỉ phương \(\overrightarrow {{u_2}} = \left( {1; - 2;3} \right)\).
Vì \(\overrightarrow {{u_1}} = \overrightarrow {{u_2}} \) nên \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \).
Lại có: \(\frac{{3 - 1}}{1} \ne \frac{{0 - 2}}{{ - 2}} \ne \frac{1}{3}\) nên điểm \({A_1}\left( {3;0;1} \right)\) không thuộc đường thẳng \({\Delta _2}\).
Do đó, hai đường thẳng \({\Delta _1},{\Delta _2}\) song song với nhau.
Trả lời câu hỏi Luyện tập 9 trang 47 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1}:\frac{{x - 1}}{1} = \frac{{y + 2}}{1} = \frac{{z - 3}}{4}\) và \({\Delta _2}:\frac{{x + 1}}{1} = \frac{{y + 1}}{1} = \frac{z}{4}\). Chứng minh rằng:
a) Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) song song với nhau;
b) Đường thẳng \({\Delta _1}\) và trục Ox chéo nhau;
c) Đường thẳng \({\Delta _2}\) trùng với đường thẳng \({\Delta _3}:\frac{{x + 2}}{1} = \frac{{y + 2}}{1} = \frac{{z + 4}}{4}\);
d) Đường thẳng \({\Delta _2}\) cắt trục Oz.
Phương pháp giải:
Sử dụng kiến thức về vị trí tương đối của hai đường thẳng để chứng minh: Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}\left( {{x_1};{y_1};{z_1}} \right),{A_2}\left( {{x_2};{y_2};{z_2}} \right)\) và tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\). Khi đó:
\({\Delta _1}//{\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1}\not \in {\Delta _2}\)
\({\Delta _1} \equiv {\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1} \in {\Delta _2}\)
\({\Delta _1}\) và \({\Delta _2}\) chéo nhau \( \Leftrightarrow \overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\)
\({\Delta _1}\) và \({\Delta _2}\) cắt nhau \( \Leftrightarrow \left\{ \begin{array}{l}\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \\\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\end{array} \right.\)
Lời giải chi tiết:
Đường thẳng \({\Delta _1}\) đi qua điểm \({A_1}\left( {1; - 2;3} \right)\) và có một vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {1;1;4} \right)\).
Đường thẳng \({\Delta _2}\) đi qua điểm \({A_2}\left( { - 1; - 1;0} \right)\) và có một vectơ chỉ phương \(\overrightarrow {{u_2}} = \left( {1;1;4} \right)\).
a) Vì \(\overrightarrow {{u_1}} = \overrightarrow {{u_2}} \) nên \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \).
Lại có: \(\frac{{1 + 1}}{1} \ne \frac{{ - 2 + 1}}{1}\) nên điểm \({A_1}\left( {1; - 2;3} \right)\) không thuộc đường thẳng \({\Delta _2}\).
Do đó, hai đường thẳng \({\Delta _1},{\Delta _2}\) song song với nhau.
b) Trục Ox có một vectơ chỉ phương \(\overrightarrow i = \left( {1;0;0} \right)\) và đi qua điểm O(0;0;0).
Ta có: \(\left[ {\overrightarrow {{u_1}} ;\overrightarrow i } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&4\\0&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}4&1\\0&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}1&1\\1&0\end{array}} \right|} \right) = \left( {0;4; - 1} \right)\), \(\overrightarrow {{A_1}O} \left( { - 1;2; - 3} \right)\)
Vì \(\overrightarrow {{A_1}O} .\left[ {\overrightarrow {{u_1}} ;\overrightarrow i } \right] = - 1.0 + 2.4 - 3.\left( { - 1} \right) = 11 \ne 0\) nên \({\Delta _1}\) và Ox chéo nhau.
c) Đường thẳng \({\Delta _3}\) có một vectơ chỉ phương \(\overrightarrow {{u_3}} = \left( {1;1;4} \right)\).
Vì \(\overrightarrow {{u_3}} = \overrightarrow {{u_2}} \) nên \(\overrightarrow {{u_3}} \) cùng phương với \(\overrightarrow {{u_2}} \).
Lại có: \(\frac{{ - 1 + 2}}{1} = \frac{{ - 1 + 2}}{1} = \frac{{0 + 4}}{4}\) nên điểm \({A_2}\left( { - 1; - 1;0} \right)\) thuộc đường thẳng \({\Delta _3}\).
Do đó, đường thẳng \({\Delta _2}\) trùng với đường thẳng \({\Delta _3}\).
d) Trục Oz có một vectơ chỉ phương \(\overrightarrow k = \left( {0;0;1} \right)\) và đi qua điểm O(0;0;0)
Ta có: \(\left[ {\overrightarrow {{u_2}} ,\overrightarrow k } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&4\\0&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}4&1\\1&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}1&1\\0&0\end{array}} \right|} \right) = \left( {1; - 1;0} \right)\), \(\overrightarrow {{A_2}O} \left( {1;1;0} \right)\)
Vì \(\overrightarrow {{A_2}O} .\left[ {\overrightarrow {{u_2}} ,\overrightarrow k } \right] = 1.1 - 1.1 - 0.0 = 0\) và \(\left[ {\overrightarrow {{u_2}} ,\overrightarrow k } \right] = \left( {1; - 1;0} \right) \ne \overrightarrow 0 \) nên \({\Delta _2}\) cắt trục Oz.
Trả lời câu hỏi Luyện tập 10 trang 48 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, xét vị trí tương đối giữa hai đường thẳng: \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + t\\z = 1 - t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = s\\y = 1 + 2s\\z = 3s\end{array} \right.\).
Phương pháp giải:
Sử dụng kiến thức về vị trí tương đối của hai đường thẳng để tìm vị trí tương đối của \({\Delta _1}\) và \({\Delta _2}\): Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\) và có phương trình tham số: \({\Delta _1}:\left\{ \begin{array}{l}x = {x_1} + {a_1}t\\y = {y_1} + {b_1}t\\z = {z_1} + {c_1}t\end{array} \right.\) \({\Delta _2}:\left\{ \begin{array}{l}x = {x_2} + {a_2}s\\y = {y_2} + {b_2}s\\z = {z_2} + {c_2}s\end{array} \right.\). Xét hệ phương trình hai ẩn t, s: \(\left\{ \begin{array}{l}{x_1} + {a_1}t = {x_2} + {a_2}s\\{y_1} + {b_1}t = {y_2} + {b_2}s\\{z_1} + {c_1}t = {z_2} + {c_2}s\end{array} \right.\left( * \right)\)
\({\Delta _1}//{\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và hệ (*) vô nghiệm.
\({\Delta _1} \equiv {\Delta _2} \Leftrightarrow \) Hệ (*) có vô số nghiệm.
\({\Delta _1}\) và \({\Delta _2}\) chéo nhau \( \Leftrightarrow \)\(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương và hệ (*) vô nghiệm.
\({\Delta _1}\) và \({\Delta _2}\) cắt nhau \( \Leftrightarrow \) Hệ (*) có nghiệm duy nhất
Lời giải chi tiết:
\({\Delta _1}\) và \({\Delta _2}\) có vectơ chỉ phương lần lượt là \(\overrightarrow {{u_1}} = \left( {2;1; - 1} \right)\) và \(\overrightarrow {{u_2}} = \left( {1;2;3} \right)\)
Vì \(\frac{2}{1} \ne \frac{1}{2}\) nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương. Do đó, \({\Delta _1}\) và \({\Delta _2}\) cắt nhau hoặc chéo nhau.
Xét hệ phương trình: \(\left\{ \begin{array}{l}1 + 2t = s\\3 + t = 1 + 2s\\1 - t = 3s\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}s - 2t = 1\;\left( 1 \right)\\2s - t = 2\;\left( 2 \right)\\3s + t = 1\;\left( 3 \right)\end{array} \right.\)
Từ (1) và (2) ta có: \(s = 1;t = 0\), thay vào (3) ta thấy không thỏa mãn phương trình.
Do đó, hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) chéo nhau.
Trả lời câu hỏi Vận dụng 3 trang 48 SGK Toán 12 Kết nối tri thức
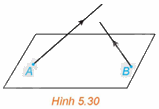
(H.5.30) Trong không gian Oxyz, có hai vật thể lần lượt xuất phát từ A(1; 2; 0) và B(3; 5; 0) với vận tốc không đổi tương ứng là \(\overrightarrow {{v_1}} = \left( {2;1;3} \right),\overrightarrow {{v_2}} = \left( {1;2;1} \right)\). Hỏi trong quá trình chuyển động, hai vật thể trên có va chạm vào nhau hay không?
Phương pháp giải:
Sử dụng kiến thức về vị trí tương đối của hai đường thẳng để giải: Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}\left( {{x_1};{y_1};{z_1}} \right),{A_2}\left( {{x_2};{y_2};{z_2}} \right)\) và tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\). Khi đó:
\({\Delta _1}//{\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1}\not \in {\Delta _2}\).
\({\Delta _1} \equiv {\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1} \in {\Delta _2}\).
\({\Delta _1}\) và \({\Delta _2}\) chéo nhau \( \Leftrightarrow \overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\).
\({\Delta _1}\) và \({\Delta _2}\) cắt nhau \( \Leftrightarrow \left\{ \begin{array}{l}\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \\\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\end{array} \right.\) .
Lời giải chi tiết:
Gọi d là đường thẳng đi qua A và có vectơ chỉ phương là \(\overrightarrow {{v_1}} =\left( {2;1;3} \right)\).
Gọi d’ là đường thẳng đi qua B và có vectơ chỉ phương là \(\overrightarrow {{v_2}} =\left( {1;2;1} \right)\).
Vì \(\frac{2}{1} \ne \frac{1}{2}\) nên hai vectơ \(\overrightarrow {{v_1}} \) và \(\overrightarrow {{v_2}} \) không cùng phương.
Ta có: \(\left[ {\overrightarrow {{v_1}} ;\overrightarrow {{v_2}} } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&3\\2&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}3&2\\1&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}2&1\\1&2\end{array}} \right|} \right) = \left( { - 5;1;3} \right) \ne \overrightarrow 0 \), \(\overrightarrow {AB} \left( {2;3;0} \right)\).
Vì \(\overrightarrow {AB} .\left[ {\overrightarrow {{v_1}} ;\overrightarrow {{v_2}} } \right] = \left( { - 5} \right).2 + 1.3 + 3.0 = - 7 \ne 0\) nên d và d’ chéo nhau.
Do đó, hai vật trên không va chạm vào nhau.
Mục 3 trong SGK Toán 12 tập 2 Kết nối tri thức thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải vận dụng kiến thức đã học để giải quyết các bài toán thực tế. Việc nắm vững lý thuyết và phương pháp giải là yếu tố then chốt để hoàn thành tốt các bài tập này.
Bài 1 thường là bài tập áp dụng trực tiếp công thức hoặc định lý đã học. Để giải bài này, học sinh cần xác định đúng các yếu tố đầu vào và áp dụng công thức phù hợp. Ví dụ, nếu bài toán liên quan đến đạo hàm, học sinh cần nhớ các quy tắc tính đạo hàm của các hàm số cơ bản.
Bài 2 có thể là bài tập nâng cao hơn, đòi hỏi học sinh phải kết hợp nhiều kiến thức khác nhau. Trong trường hợp này, học sinh cần phân tích bài toán một cách kỹ lưỡng, xác định các mối liên hệ giữa các yếu tố và tìm ra phương pháp giải phù hợp.
Bài 3 thường là bài tập tổng hợp, kiểm tra khả năng vận dụng kiến thức của học sinh vào thực tế. Để giải bài này, học sinh cần có tư duy logic, khả năng phân tích và tổng hợp thông tin.
Bài toán: Tính đạo hàm của hàm số y = x2 + 2x - 1.
Giải:
Áp dụng quy tắc tính đạo hàm của hàm số đa thức, ta có:
y' = 2x + 2
Ngoài SGK, học sinh có thể tham khảo thêm các tài liệu sau:
Việc giải bài tập mục 3 trang 46,47,48 SGK Toán 12 tập 2 Kết nối tri thức đòi hỏi sự kiên trì, cẩn thận và nắm vững kiến thức. Hy vọng với những hướng dẫn chi tiết và phương pháp giải hiệu quả trên đây, các em sẽ tự tin hơn trong quá trình học tập và đạt được kết quả tốt nhất.