Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 1.9 trang 14 SGK Toán 12 tập 1 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hóa bằng hàm số (fleft( t right) = frac{{5;000}}{{1 + 5{e^{ - t}}}},t ge 0,) trong đó thời gian t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f’(t) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?
Đề bài
Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hóa bằng hàm số \(f\left( t \right) = \frac{{5\;000}}{{1 + 5{e^{ - t}}}},t \ge 0,\) trong đó thời gian t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f’(t) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về cách tìm cực trị của hàm số để tìm cực trị của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Lời giải chi tiết
Ta có: \(f'\left( t \right) = \frac{{ - 5000\left( {1 + 5{e^{ - t}}} \right)'}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^2}}} = \frac{{25\;000{e^{ - t}}}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^2}}}\)
Tốc độ bán hàng là lớn nhất khi \(f'\left( t \right)\) lớn nhất.
Đặt \(h\left( t \right) = \frac{{25\;000{e^{ - t}}}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^2}}}\).
\(h'\left( t \right) = \frac{{ - 25\;000{e^{ - t}}{{\left( {1 + 5{e^{ - t}}} \right)}^2} - 2.\left( { - 5{e^{ - t}}} \right).\left( {1 + 5{e^{ - t}}} \right).25\;000{e^{ - t}}}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^4}}}\)
\( = \frac{{ - 25\;000{e^{ - t}}\left( {1 + 5{e^{ - t}}} \right)\left( {1 + 5{e^{ - t}} - 10{e^{ - t}}} \right)}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^4}}} = \frac{{ - 25\;000{e^{ - t}}\left( {1 - 5{e^{ - t}}} \right)}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^3}}}\)
\(h'\left( t \right) = 0 \Leftrightarrow \frac{{ - 25\;000{e^{ - t}}\left( {1 - 5{e^{ - t}}} \right)}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^3}}} = 0 \Leftrightarrow 1 - 5{e^{ - t}} = 0 \Leftrightarrow {e^{ - t}} = \frac{1}{5} \Leftrightarrow t = \ln 5\) (tm)
Ta có bảng biến thiên với \(t \in \left[ {0; + \infty } \right)\):
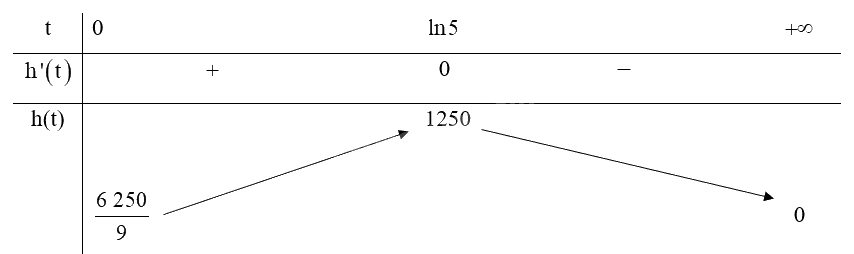
Vậy sau khi phát hành khoảng \(\ln 5 \approx 1,6\) năm thì thì tốc độ bán hàng là lớn nhất.
Bài tập 1.9 trang 14 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương 1: Hàm số và đồ thị. Bài tập này thường liên quan đến việc xác định tập xác định của hàm số, tìm tập giá trị, và phân tích tính đơn điệu của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hàm số, các phép biến đổi hàm số, và các phương pháp giải phương trình, bất phương trình.
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, đề bài sẽ yêu cầu chúng ta xác định một tập hợp nào đó (tập xác định, tập giá trị) hoặc chứng minh một tính chất nào đó của hàm số. Việc phân tích đề bài một cách cẩn thận sẽ giúp chúng ta lựa chọn phương pháp giải phù hợp và tránh những sai sót không đáng có.
Có nhiều phương pháp khác nhau để giải bài tập 1.9, tùy thuộc vào dạng bài cụ thể. Dưới đây là một số phương pháp thường được sử dụng:
Giả sử bài tập 1.9 yêu cầu chúng ta tìm tập xác định của hàm số f(x) = √(x-2) / (x+1).
Khi giải bài tập 1.9, bạn cần lưu ý những điều sau:
Để củng cố kiến thức, bạn có thể làm thêm một số bài tập tương tự sau:
Bài tập 1.9 trang 14 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số. Hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải hiệu quả mà chúng tôi đã cung cấp, bạn sẽ có thể giải bài tập này một cách dễ dàng và tự tin.
| Khái niệm | Giải thích |
|---|---|
| Tập xác định | Tập hợp tất cả các giá trị của x sao cho hàm số f(x) có nghĩa. |
| Tập giá trị | Tập hợp tất cả các giá trị của f(x) khi x thuộc tập xác định. |
| Hàm số đơn điệu | Hàm số được gọi là đơn điệu nếu nó luôn tăng hoặc luôn giảm trên một khoảng nào đó. |