Bài tập 4.8 trang 18 SGK Toán 12 tập 2 thuộc chương trình học Toán 12 Kết nối tri thức. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 4.8, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Sử dụng ý nghĩa hình học của tích phân, tính: a) \(\int\limits_1^2 {\left( {2x + 1} \right)dx} \); b) \(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} dx} \).
Đề bài
Sử dụng ý nghĩa hình học của tích phân, tính:
a) \(\int\limits_1^2 {\left( {2x + 1} \right)dx} \);
b) \(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} dx} \).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về ý nghĩa hình học của tích phân để tính: Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b], thì tích phân \(\int\limits_a^b {f\left( x \right)dx} \) là diện tích S của hình thang cong giới hạn bởi đồ thị \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\). Vậy \(S = \int\limits_a^b {f\left( x \right)dx} \).
Lời giải chi tiết
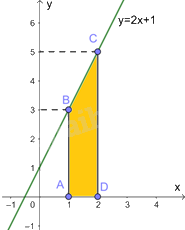
a) Tích phân cần tính là diện tích của hình thang vuông ABCD, có đáy nhỏ \(AB = 3,\) đáy lớn \(CD = 5\) và đường cao \(AD = 1\).
Do đó, \(\int\limits_1^2 {\left( {2x + 1} \right)dx} = {S_{ABCD}} = \frac{1}{2}\left( {AB + CD} \right)AD = \frac{1}{2}\left( {3 + 5} \right).1 = 4\)
b) Ta có \(y = \sqrt {9 - {x^2}} \) là phương trình nửa phía trên trục hoành của đường tròn tâm tại gốc tọa độ O và bán kính 3. Do đó, tích phân cần tính là diện tích nửa phía trên trục hoành của hình tròn tương ứng.
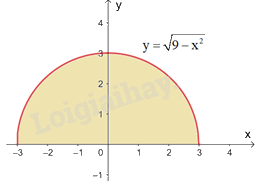
Vậy \(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} dx} = \frac{9}{2}\pi \)
Bài tập 4.8 trang 18 SGK Toán 12 tập 2 - Kết nối tri thức là một bài toán quan trọng trong chương trình học về đạo hàm. Bài toán này thường yêu cầu học sinh áp dụng các quy tắc tính đạo hàm của các hàm số cơ bản, kết hợp với các kỹ năng biến đổi đại số để tìm ra kết quả chính xác.
Trước khi đi vào giải bài tập, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các thông tin đã cho. Thông thường, đề bài sẽ cung cấp một hàm số và yêu cầu tính đạo hàm của hàm số đó tại một điểm cụ thể hoặc tìm điều kiện để đạo hàm bằng một giá trị cho trước.
Để giải bài tập 4.8 trang 18 SGK Toán 12 tập 2 - Kết nối tri thức một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
(Giả sử đề bài là: Cho hàm số f(x) = x^3 - 3x^2 + 2. Tính f'(x) và tìm các điểm cực trị của hàm số.)
f'(x) = 3x^2 - 6x
Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:
3x^2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Ta xét dấu của f'(x) trên các khoảng:
Vậy, hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.
Để hiểu rõ hơn về cách giải bài tập 4.8, chúng ta hãy xem xét một ví dụ minh họa khác:
(Ví dụ: Cho hàm số g(x) = sin(2x). Tính g'(x).)
Lời giải:
g'(x) = 2cos(2x)
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, các em học sinh có thể luyện tập thêm các bài tập sau:
Bài tập 4.8 trang 18 SGK Toán 12 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm và ứng dụng đạo hàm vào giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ nắm vững kiến thức và tự tin làm bài tập.