Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 Kết nối tri thức tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Mục 1 của chương trình Toán 12 tập 1 tập trung vào các kiến thức cơ bản về giới hạn dãy số. Việc hiểu rõ các khái niệm và phương pháp giải bài tập trong mục này là nền tảng quan trọng cho các chương tiếp theo.
Tính đơn điệu của hàm số
Trả lời câu hỏi Luyện tập 2 trang 7 SGK Toán 12 Kết nối tri thức
Tìm các khoảng đồng biến, khoảng nghịch biến của hàm số \(y = - {x^2} + 2x + 3\).
Phương pháp giải:
Sử dụng kiến thức về định lí về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K.
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) nghịch biến trên khoảng K.
Lời giải chi tiết:
Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \(y' = - 2x + 2,y' > 0\) với \(x \in \left( { - \infty ;1} \right)\); \(y < 0\) với \(x \in \left( {1; + \infty } \right)\).
Do đó, hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và nghịch biến trên khoảng \(\left( {1; + \infty } \right)\).
Trả lời câu hỏi Hoạt động 1 trang 6 SGK Toán 12 Kết nối tri thức
Quan sát đồ thị của hàm số \(y = {x^2}\) (H.1.2)
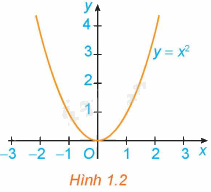
a) Hàm số đồng biến trên khoảng nào?
b) Hàm số nghịch biến trên khoảng nào?
Phương pháp giải:
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Giả sử K là một khoảng, một đoạn hoặc một nửa khoảng và \(y = f\left( x \right)\) là hàm số xác định trên K.
+ Hàm số \(y = f\left( x \right)\) được gọi là đồng biến trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\)
+ Hàm số \(y = f\left( x \right)\) được gọi là nghịch biến trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Lời giải chi tiết:
Từ đồ thị ta thấy:
+ Xét khoảng \(\left( {0; + \infty } \right)\): \(\forall {x_1},{x_2} \in \left( {0; + \infty } \right),{x_1} < {x_2}\) thì \(x_1^2 < x_2^2\) hay \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Suy ra, hàm số \(y = {x^2}\) đồng biến trên \(\left( {0; + \infty } \right)\).
+ Xét khoảng \(\left( { - \infty ;0} \right)\): \(\forall {x_1},{x_2} \in \left( { - \infty ;0} \right),{x_1} < {x_2}\) thì \(x_1^2 > x_2^2\)hay \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
Suy ra, hàm số \(y = {x^2}\) nghịch biến trên \(\left( { - \infty ;0} \right)\).
Trả lời câu hỏi Hoạt động 3 trang 7 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\).
a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm x mà \(f'\left( x \right) = 0\).
b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.
c) Nếu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Phương pháp giải:
Cho hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\).
a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm x mà \(f'\left( x \right) = 0\).
b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.
c) Nếu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
a) \(f'\left( x \right) = \left( {{x^3} - 3{x^2} + 2x + 1} \right)' = 3{x^2} - 6x + 2\)
\(f'\left( x \right) = 0 \Leftrightarrow 3{x^2} - 6x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{3 - \sqrt 3 }}{3}\\x = \frac{{3 + \sqrt 3 }}{3}\end{array} \right.\)
Vậy \(x = \frac{{3 - \sqrt 3 }}{3},x = \frac{{3 + \sqrt 3 }}{3}\) thì \(f'\left( x \right) = 0\)
b) Bảng biến thiên:
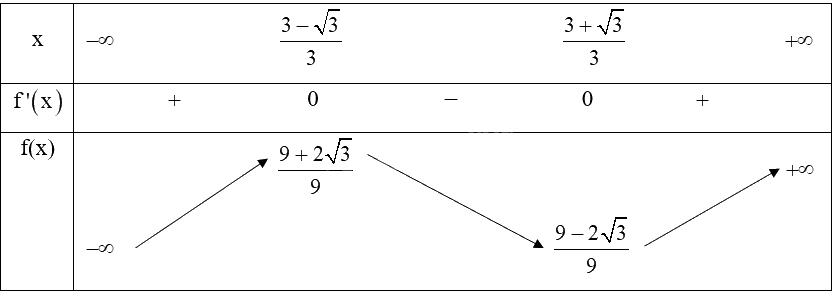
c) Hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\) đồng biến trên khoảng \(\left( { - \infty ;\frac{{3 - \sqrt 3 }}{3}} \right)\) và \(\left( {\frac{{3 + \sqrt 3 }}{3}; + \infty } \right)\).
Hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\) nghịch biến trên khoảng \(\left( {\frac{{3 - \sqrt 3 }}{3};\frac{{3 + \sqrt 3 }}{3}} \right)\).
Trả lời câu hỏi Vận dụng 1 trang 9 SGK Toán 12 Kết nối tri thức
Giải bài toán trong tình huống mở đầu bằng cách thực hiện lần lượt các yêu cầu sau:
a) Theo ý nghĩa cơ học của đạo hàm, vận tốc v(t) là đạo hàm của s(t). Hãy tìm vận tốc v(t).
b) Xét dấu của hàm v(t), từ đó suy ra câu trả lời.
Bài toán mở đầu:
Xét một chất điểm chuyển động trên một trục số nằm ngang, chiều dương từ trái sang phải (H.1.1). Giả sử vị trí s(t) (mét) của chất điểm trên trục số đã chọn tại thời điểm t (giây) được cho bởi công thức \(s\left( t \right) = {t^3} - 9{t^2} + 15t,t \ge 0\). Hỏi trong khoảng thời gian nào thì chất điểm chuyển động sang phải, trong khoảng thời gian nào thì chất điểm chuyển động sang trái?
Phương pháp giải:
a) Sử dụng kiến thức về ý nghĩa cơ học của đạo hàm để tìm hàm vận tốc: Theo ý nghĩa cơ học, vận tốc v(t) là đạo hàm của hàm số s(t).
b) Chất điểm chuyển động theo chiều dương khi \(v\left( t \right) > 0\).
Chất điểm chuyển động theo chiều âm khi \(v\left( t \right) < 0\)
Lời giải chi tiết:
a) Ta có: \(v\left( t \right) = s'\left( t \right) = \left( {{t^3} - 9{t^2} + 15t} \right)' = 3{t^2} - 18t + 15\)
b) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(v\left( t \right) > 0 \Leftrightarrow 3{t^2} - 18t + 15 > 0 \Leftrightarrow \left( {t - 1} \right)\left( {t - 5} \right) > 0 \Leftrightarrow \left[ \begin{array}{l}t < 1\\t > 5\end{array} \right.\)
\(v\left( t \right) < 0 \Leftrightarrow 3{t^2} - 18t + 15 < 0 \Leftrightarrow \left( {t - 1} \right)\left( {t - 5} \right) < 0 \Leftrightarrow 1 < t < 5\)
Chất điểm chuyển động theo chiều dương (sang bên phải) khi \(v\left( t \right) > 0\), tức là \(t \in \left( { - \infty ;1} \right) \cup \left( {5; + \infty } \right)\).
Chất điểm chuyển động theo chiều âm (sang bên trái) khi \(v\left( t \right) < 0\), tức là \(1 < t < 5\).
Trả lời câu hỏi Luyện tập 1 trang 6 SGK Toán 12 Kết nối tri thức
Hình 1.5 là đồ thị của hàm số \(y = {x^3} - 3{x^2} + 2\). Hãy tìm các khoảng đồng biến, khoảng nghịch biến của hàm số.
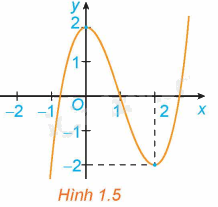
Phương pháp giải:
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến:
+ Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải.
+ Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải.
Lời giải chi tiết:
Tập xác định của hàm số là \(\mathbb{R}\).
Trong khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\) thì đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) đi lên từ trái sang phải nên hàm số \(y = {x^3} - 3{x^2} + 2\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\).
Trong khoảng \(\left( {0;2} \right)\) thì đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) đi xuống từ trái sang phải nên hàm số \(y = {x^3} - 3{x^2} + 2\) nghịch biến trên khoảng \(\left( {0;2} \right)\).
Trả lời câu hỏi Hoạt động 2 trang 6 SGK Toán 12 Kết nối tri thức
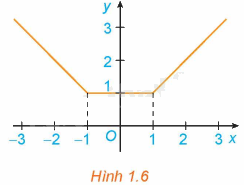
a) Xét dấu đạo hàm của hàm số trên các khoảng \(\left( { - \infty ; - 1} \right)\), \(\left( {1; + \infty } \right)\). Nêu nhận xét về mối quan hệ giữa tính đồng biến, nghịch biến và dấu của đạo hàm trên mỗi khoảng này.
b) Có nhận xét gì về đạo hàm y’ của hàm số y trên khoảng \(\left( { - 1;1} \right)\)?
Phương pháp giải:
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm nhận xét:
+ Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải.
+ Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải.
Lời giải chi tiết:
a) + Xét khoảng \(\left( { - \infty ; - 1} \right)\) ta có: \(y' = \left( { - x} \right)' = - 1 < 0\)
Trong khoảng \(\left( { - \infty ; - 1} \right)\) ta thấy hàm số y nghịch biến và đạo hàm \(y' < 0\).
+ Xét khoảng \(\left( {1; + \infty } \right)\) ta có: \(y' = x' = 1 > 0\)
Trong khoảng \(\left( {1; + \infty } \right)\) ta thấy hàm số y đồng biến và đạo hàm \(y' > 0\).
b) Trong khoảng \(\left( { - 1;1} \right)\) ta có: \(y' = \left( 1 \right)' = 0\)
Trong khoảng \(\left( { - 1;1} \right)\) ta thấy hàm số y không đổi và đạo hàm \(y' = 0\).
Trả lời câu hỏi Luyện tập 3 trang 9 SGK Toán 12 Kết nối tri thức
Tìm các khoảng đơn điệu của các hàm số sau:
a) \(y = \frac{1}{3}{x^3} + 3{x^2} + 5x + 2\);
b) \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\).
Phương pháp giải:
- Sử dụng kiến thức về các bước để xét tính đơn điệu của hàm số để tìm khoảng đơn điệu của hàm số: Các bước để xét tính đơn điệu của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm \(f'\left( x \right)\). Tìm các điểm \({x_i}\left( {i = 1,2,...} \right)\) mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
3. Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên của hàm số.
4. Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
a) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = {x^2} + 6x + 5,y' = 0 \Leftrightarrow {x^2} + 6x + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 5\end{array} \right.\)
Lập bảng biến thiên của hàm số:
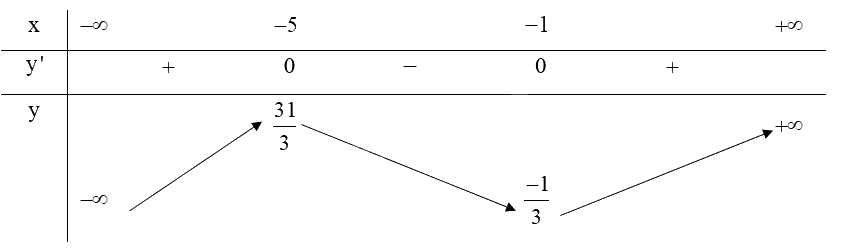
Hàm số \(y = \frac{1}{3}{x^3} + 3{x^2} + 5x + 2\) đồng biến trên khoảng \(\left( { - \infty ; - 5} \right)\) và \(\left( { - 1; + \infty } \right)\).
Hàm số \(y = \frac{1}{3}{x^3} + 3{x^2} + 5x + 2\) nghịch biến trên khoảng \(\left( { - 5; - 1} \right)\).
b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).
Ta có: \(y' = \frac{{\left( { - 2x + 5} \right)\left( {x - 2} \right) - \left( { - {x^2} + 5x - 7} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{ - {x^2} + 4x - 3}}{{{{\left( {x - 2} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\) (thỏa mãn)
Lập bảng biến thiên của hàm số:
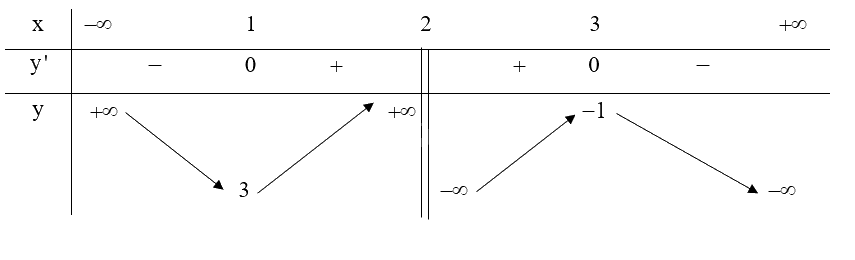Hàm số \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\) đồng biến trên khoảng \(\left( {1;2} \right)\) và \(\left( {2;3} \right)\).
Hàm số \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\) nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\).
Trả lời câu hỏi Hoạt động 1 trang 6 SGK Toán 12 Kết nối tri thức
Quan sát đồ thị của hàm số \(y = {x^2}\) (H.1.2)
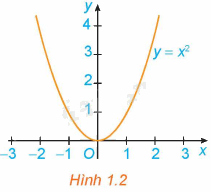
a) Hàm số đồng biến trên khoảng nào?
b) Hàm số nghịch biến trên khoảng nào?
Phương pháp giải:
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Giả sử K là một khoảng, một đoạn hoặc một nửa khoảng và \(y = f\left( x \right)\) là hàm số xác định trên K.
+ Hàm số \(y = f\left( x \right)\) được gọi là đồng biến trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\)
+ Hàm số \(y = f\left( x \right)\) được gọi là nghịch biến trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Lời giải chi tiết:
Từ đồ thị ta thấy:
+ Xét khoảng \(\left( {0; + \infty } \right)\): \(\forall {x_1},{x_2} \in \left( {0; + \infty } \right),{x_1} < {x_2}\) thì \(x_1^2 < x_2^2\) hay \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Suy ra, hàm số \(y = {x^2}\) đồng biến trên \(\left( {0; + \infty } \right)\).
+ Xét khoảng \(\left( { - \infty ;0} \right)\): \(\forall {x_1},{x_2} \in \left( { - \infty ;0} \right),{x_1} < {x_2}\) thì \(x_1^2 > x_2^2\)hay \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
Suy ra, hàm số \(y = {x^2}\) nghịch biến trên \(\left( { - \infty ;0} \right)\).
Trả lời câu hỏi Luyện tập 1 trang 6 SGK Toán 12 Kết nối tri thức
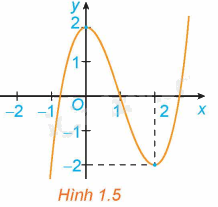
Hình 1.5 là đồ thị của hàm số \(y = {x^3} - 3{x^2} + 2\). Hãy tìm các khoảng đồng biến, khoảng nghịch biến của hàm số.
Phương pháp giải:
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến:
+ Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải.
+ Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải.
Lời giải chi tiết:
Tập xác định của hàm số là \(\mathbb{R}\).
Trong khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\) thì đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) đi lên từ trái sang phải nên hàm số \(y = {x^3} - 3{x^2} + 2\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\).
Trong khoảng \(\left( {0;2} \right)\) thì đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) đi xuống từ trái sang phải nên hàm số \(y = {x^3} - 3{x^2} + 2\) nghịch biến trên khoảng \(\left( {0;2} \right)\).
Trả lời câu hỏi Hoạt động 2 trang 6 SGK Toán 12 Kết nối tri thức
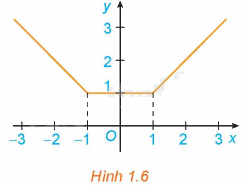
a) Xét dấu đạo hàm của hàm số trên các khoảng \(\left( { - \infty ; - 1} \right)\), \(\left( {1; + \infty } \right)\). Nêu nhận xét về mối quan hệ giữa tính đồng biến, nghịch biến và dấu của đạo hàm trên mỗi khoảng này.
b) Có nhận xét gì về đạo hàm y’ của hàm số y trên khoảng \(\left( { - 1;1} \right)\)?
Phương pháp giải:
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm nhận xét:
+ Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải.
+ Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải.
Lời giải chi tiết:
a) + Xét khoảng \(\left( { - \infty ; - 1} \right)\) ta có: \(y' = \left( { - x} \right)' = - 1 < 0\)
Trong khoảng \(\left( { - \infty ; - 1} \right)\) ta thấy hàm số y nghịch biến và đạo hàm \(y' < 0\).
+ Xét khoảng \(\left( {1; + \infty } \right)\) ta có: \(y' = x' = 1 > 0\)
Trong khoảng \(\left( {1; + \infty } \right)\) ta thấy hàm số y đồng biến và đạo hàm \(y' > 0\).
b) Trong khoảng \(\left( { - 1;1} \right)\) ta có: \(y' = \left( 1 \right)' = 0\)
Trong khoảng \(\left( { - 1;1} \right)\) ta thấy hàm số y không đổi và đạo hàm \(y' = 0\).
Trả lời câu hỏi Luyện tập 2 trang 7 SGK Toán 12 Kết nối tri thức
Tìm các khoảng đồng biến, khoảng nghịch biến của hàm số \(y = - {x^2} + 2x + 3\).
Phương pháp giải:
Sử dụng kiến thức về định lí về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K.
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) nghịch biến trên khoảng K.
Lời giải chi tiết:
Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \(y' = - 2x + 2,y' > 0\) với \(x \in \left( { - \infty ;1} \right)\); \(y < 0\) với \(x \in \left( {1; + \infty } \right)\).
Do đó, hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và nghịch biến trên khoảng \(\left( {1; + \infty } \right)\).
Trả lời câu hỏi Hoạt động 3 trang 7 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\).
a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm x mà \(f'\left( x \right) = 0\).
b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.
c) Nếu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Phương pháp giải:
Cho hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\).
a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm x mà \(f'\left( x \right) = 0\).
b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.
c) Nếu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
a) \(f'\left( x \right) = \left( {{x^3} - 3{x^2} + 2x + 1} \right)' = 3{x^2} - 6x + 2\)
\(f'\left( x \right) = 0 \Leftrightarrow 3{x^2} - 6x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{3 - \sqrt 3 }}{3}\\x = \frac{{3 + \sqrt 3 }}{3}\end{array} \right.\)
Vậy \(x = \frac{{3 - \sqrt 3 }}{3},x = \frac{{3 + \sqrt 3 }}{3}\) thì \(f'\left( x \right) = 0\)
b) Bảng biến thiên:
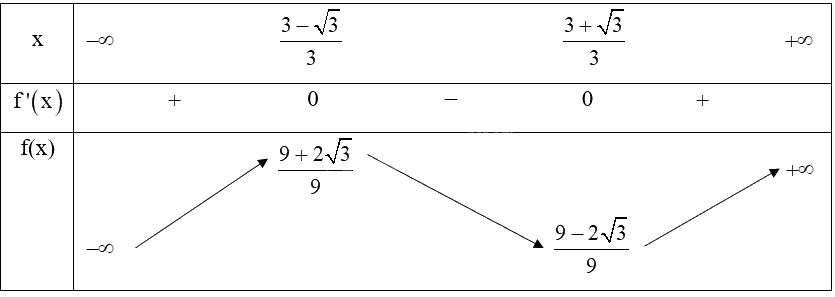
c) Hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\) đồng biến trên khoảng \(\left( { - \infty ;\frac{{3 - \sqrt 3 }}{3}} \right)\) và \(\left( {\frac{{3 + \sqrt 3 }}{3}; + \infty } \right)\).
Hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\) nghịch biến trên khoảng \(\left( {\frac{{3 - \sqrt 3 }}{3};\frac{{3 + \sqrt 3 }}{3}} \right)\).
Trả lời câu hỏi Luyện tập 3 trang 9 SGK Toán 12 Kết nối tri thức
Tìm các khoảng đơn điệu của các hàm số sau:
a) \(y = \frac{1}{3}{x^3} + 3{x^2} + 5x + 2\);
b) \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\).
Phương pháp giải:
- Sử dụng kiến thức về các bước để xét tính đơn điệu của hàm số để tìm khoảng đơn điệu của hàm số: Các bước để xét tính đơn điệu của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm \(f'\left( x \right)\). Tìm các điểm \({x_i}\left( {i = 1,2,...} \right)\) mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
3. Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên của hàm số.
4. Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
a) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = {x^2} + 6x + 5,y' = 0 \Leftrightarrow {x^2} + 6x + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 5\end{array} \right.\)
Lập bảng biến thiên của hàm số:
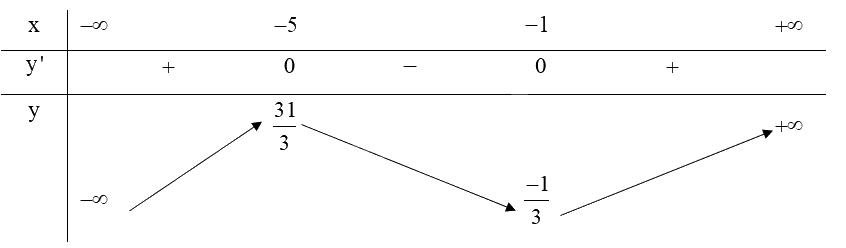
Hàm số \(y = \frac{1}{3}{x^3} + 3{x^2} + 5x + 2\) đồng biến trên khoảng \(\left( { - \infty ; - 5} \right)\) và \(\left( { - 1; + \infty } \right)\).
Hàm số \(y = \frac{1}{3}{x^3} + 3{x^2} + 5x + 2\) nghịch biến trên khoảng \(\left( { - 5; - 1} \right)\).
b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).
Ta có: \(y' = \frac{{\left( { - 2x + 5} \right)\left( {x - 2} \right) - \left( { - {x^2} + 5x - 7} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{ - {x^2} + 4x - 3}}{{{{\left( {x - 2} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\) (thỏa mãn)
Lập bảng biến thiên của hàm số:
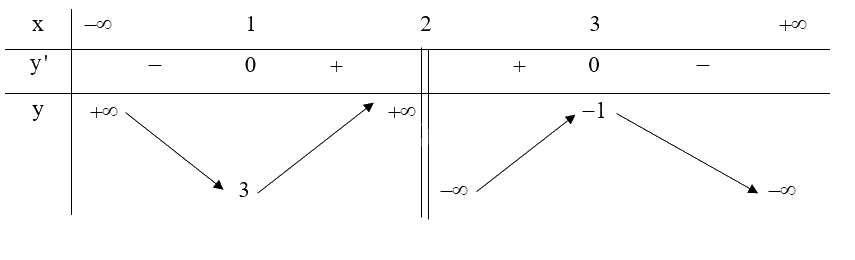Hàm số \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\) đồng biến trên khoảng \(\left( {1;2} \right)\) và \(\left( {2;3} \right)\).
Hàm số \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\) nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\).
Trả lời câu hỏi Vận dụng 1 trang 9 SGK Toán 12 Kết nối tri thức
Giải bài toán trong tình huống mở đầu bằng cách thực hiện lần lượt các yêu cầu sau:
a) Theo ý nghĩa cơ học của đạo hàm, vận tốc v(t) là đạo hàm của s(t). Hãy tìm vận tốc v(t).
b) Xét dấu của hàm v(t), từ đó suy ra câu trả lời.
Bài toán mở đầu:
Xét một chất điểm chuyển động trên một trục số nằm ngang, chiều dương từ trái sang phải (H.1.1). Giả sử vị trí s(t) (mét) của chất điểm trên trục số đã chọn tại thời điểm t (giây) được cho bởi công thức \(s\left( t \right) = {t^3} - 9{t^2} + 15t,t \ge 0\). Hỏi trong khoảng thời gian nào thì chất điểm chuyển động sang phải, trong khoảng thời gian nào thì chất điểm chuyển động sang trái?
Phương pháp giải:
a) Sử dụng kiến thức về ý nghĩa cơ học của đạo hàm để tìm hàm vận tốc: Theo ý nghĩa cơ học, vận tốc v(t) là đạo hàm của hàm số s(t).
b) Chất điểm chuyển động theo chiều dương khi \(v\left( t \right) > 0\).
Chất điểm chuyển động theo chiều âm khi \(v\left( t \right) < 0\)
Lời giải chi tiết:
a) Ta có: \(v\left( t \right) = s'\left( t \right) = \left( {{t^3} - 9{t^2} + 15t} \right)' = 3{t^2} - 18t + 15\)
b) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(v\left( t \right) > 0 \Leftrightarrow 3{t^2} - 18t + 15 > 0 \Leftrightarrow \left( {t - 1} \right)\left( {t - 5} \right) > 0 \Leftrightarrow \left[ \begin{array}{l}t < 1\\t > 5\end{array} \right.\)
\(v\left( t \right) < 0 \Leftrightarrow 3{t^2} - 18t + 15 < 0 \Leftrightarrow \left( {t - 1} \right)\left( {t - 5} \right) < 0 \Leftrightarrow 1 < t < 5\)
Chất điểm chuyển động theo chiều dương (sang bên phải) khi \(v\left( t \right) > 0\), tức là \(t \in \left( { - \infty ;1} \right) \cup \left( {5; + \infty } \right)\).
Chất điểm chuyển động theo chiều âm (sang bên trái) khi \(v\left( t \right) < 0\), tức là \(1 < t < 5\).
Mục 1 của SGK Toán 12 tập 1 Kết nối tri thức giới thiệu về khái niệm giới hạn của dãy số. Đây là một khái niệm nền tảng trong giải tích, đóng vai trò quan trọng trong việc hiểu các khái niệm phức tạp hơn như đạo hàm và tích phân. Để nắm vững kiến thức này, học sinh cần hiểu rõ định nghĩa giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn.
Một dãy số (un) được gọi là có giới hạn L nếu khi n tiến tới vô cùng, các số hạng của dãy số tiến gần đến L. Ký hiệu: limn→∞ un = L. Để chứng minh một dãy số có giới hạn, ta thường sử dụng định nghĩa hoặc các tính chất của giới hạn.
Các tính chất cơ bản của giới hạn bao gồm:
Để giải các bài tập trong mục 1, học sinh cần nắm vững các phương pháp sau:
Bài 1.1 (Trang 5): Cho dãy số (un) = 2n + 1. Tính limn→∞ un.
Lời giải: limn→∞ (2n + 1) = limn→∞ 2n + limn→∞ 1 = ∞ + 1 = ∞. Vậy dãy số (un) không có giới hạn hữu hạn.
Bài 1.2 (Trang 6): Cho dãy số (vn) = 1/n. Tính limn→∞ vn.
Lời giải: limn→∞ (1/n) = 0. Vậy dãy số (vn) có giới hạn là 0.
Bài 1.3 (Trang 7): Chứng minh rằng dãy số (wn) = (n+1)/n có giới hạn là 1.
Lời giải: limn→∞ (n+1)/n = limn→∞ (1 + 1/n) = 1 + limn→∞ (1/n) = 1 + 0 = 1. Vậy dãy số (wn) có giới hạn là 1.
Để củng cố kiến thức về giới hạn dãy số, học sinh nên làm thêm các bài tập trong sách bài tập và các đề thi thử. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn trong quá trình giải bài tập.
Ngoài SGK, học sinh có thể tham khảo các tài liệu sau:
Hy vọng với những hướng dẫn chi tiết này, các em sẽ hiểu rõ hơn về giới hạn dãy số và tự tin giải các bài tập trong SGK Toán 12 tập 1 Kết nối tri thức. Chúc các em học tập tốt!
