Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 2.42 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
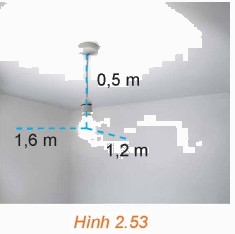
Hình 2.53 minh họa một chiếc đèn được treo cách trần nhà 0,5m, cách hai tường lần lượt là 1,2m và 1,6m. Hai bức tường vuông góc với nhau và cùng vuông góc với trần nhà. Người ta di chuyển chiếc đèn đó đến vị trí mới cách trần nhà là 0,4m, cách hai tường đều là 1,5m. a) Lập một hệ trục tọa độ Oxyz phù hợp và xác định tọa độ của bóng đèn lúc đầu và sau khi di chuyển. b) Vị trí mới của bóng đèn cách vị trí ban đầu là bao nhiêu mét? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
Đề bài
Hình 2.53 minh họa một chiếc đèn được treo cách trần nhà 0,5m, cách hai tường lần lượt là 1,2m và 1,6m. Hai bức tường vuông góc với nhau và cùng vuông góc với trần nhà. Người ta di chuyển chiếc đèn đó đến vị trí mới cách trần nhà là 0,4m, cách hai tường đều là 1,5m.a) Lập một hệ trục tọa độ Oxyz phù hợp và xác định tọa độ của bóng đèn lúc đầu và sau khi di chuyển.b) Vị trí mới của bóng đèn cách vị trí ban đầu là bao nhiêu mét? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về hệ tọa độ trong không gian để giải thích: Trong không gian, ba trục Ox, Oy, Oz đôi một vuông góc với nhau tại gốc O của mỗi trục. Gọi \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt là các vectơ đơn vị trên các trục Ox, Oy, Oz. Hệ ba trục tọa độ như vậy được gọi là hệ trục tọa độ Descartes vuông góc Oxyz (hay đơn giản là hệ tọa độ Oxyz). Điểm O được gọi là gốc tọa độ, các mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau và được gọi là các mặt phẳng tọa độ. Không gian với hệ tọa độ Oxyz còn được gọi là không gian Oxyz.
b) Sử dụng kiến thức về độ dài đoạn thẳng trong không gian để tính: Nếu \(A\left( {{x_A};{y_A};{z_A}} \right)\) và \(B\left( {{x_B};{y_B};{z_B}} \right)\) thì \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \).
Lời giải chi tiết
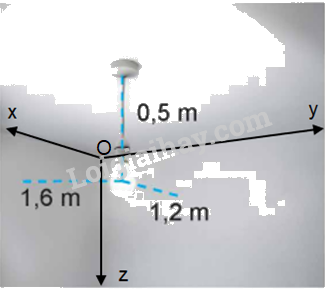
a) Chọn hệ trục tọa độ Oxyz như sau:
+ Gốc O trùng với một góc của phòng
+ Mặt phẳng (Oxy) trùng với trần nhà, mặt phẳng (Oxz) và mặt phẳng (Oyz) trùng với hai bức tường (như hình vẽ).
Tọa độ của bóng đèn lúc đầu là A(1,6; 1,2; 0,5)
Tọa độ bóng đèn sau khi di chuyển là: B(1,5; 1,5; 0,4)
Bài tập 2.42 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về đạo hàm, các quy tắc tính đạo hàm và các ứng dụng của đạo hàm trong việc giải quyết các bài toán liên quan đến sự biến thiên của hàm số.
Bài tập 2.42 thường có dạng yêu cầu tính đạo hàm của một hàm số, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số, tìm cực trị của hàm số, hoặc giải các bài toán tối ưu hóa liên quan đến hàm số. Ví dụ, bài tập có thể yêu cầu:
Để giải bài tập 2.42 một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Bài toán: Tính đạo hàm của hàm số f(x) = 2x^2 + 3x - 1 và xác định khoảng đồng biến, nghịch biến của hàm số.
Giải:
1. Tính đạo hàm:
f'(x) = 4x + 3
2. Xác định khoảng đồng biến, nghịch biến:
Khi giải bài tập 2.42, bạn cần lưu ý những điều sau:
Để học tập và ôn luyện kiến thức về đạo hàm, bạn có thể tham khảo các tài liệu sau:
Bài tập 2.42 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Hy vọng với hướng dẫn chi tiết và các phương pháp giải bài tập được trình bày trong bài viết này, bạn sẽ có thể giải quyết bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!