Bài tập 3.1 trang 78 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 3.1 trang 78 SGK Toán 12 tập 1, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Thống kê số thẻ vàng của mỗi câu lạc bộ trong giải ngoại hạng Anh mùa giải 2021-2022 cho kết quả như sau: a) Hãy ghép nhóm dãy số liệu trên thành các nhóm có độ dài bằng nhau với nhóm đầu tiên là (left[ {40;50} right)). b) Tính khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu gốc và mẫu số liệu ghép nhóm thu được ở câu a. Giá trị nào là giá trị chính xác? Giá trị nào là giá trị xấp xỉ?
Đề bài
Thống kê số thẻ vàng của mỗi câu lạc bộ trong giải ngoại hạng Anh mùa giải 2021-2022 cho kết quả như sau:
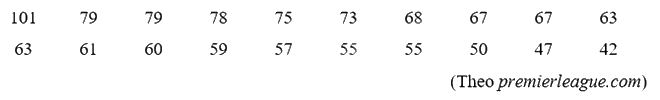
a) Hãy ghép nhóm dãy số liệu trên thành các nhóm có độ dài bằng nhau với nhóm đầu tiên là \(\left[ {40;50} \right)\).
b) Tính khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu gốc và mẫu số liệu ghép nhóm thu được ở câu a. Giá trị nào là giá trị chính xác? Giá trị nào là giá trị xấp xỉ?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về khoảng biến thiên của mẫu số liệu ghép nhóm để tính:
Cho mẫu số liệu ghép nhóm:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: \(R = {a_{k + 1}} - {a_1}\).
+ Sử dụng kiến thức về khoảng tứ phân vị của mẫu số liệu ghép nhóm để tính: Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu là \({\Delta _Q}\), là hiệu số giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).
Lời giải chi tiết
a) Bảng số liệu ghép nhóm:

b) Với mẫu số liệu gốc: Khoảng biến thiên là: \({R_1} = 101 - 42 = 59\)
Sắp xếp mẫu số liệu theo thứ tự không giảm là:
42; 47; 50; 55; 55; 57; 59; 60; 61; 63; 63; 67; 67; 68; 73; 75; 78; 79; 79; 101
Vì \(n = 20\) nên tứ phân vị thứ nhất là trung vị của dãy số liệu: 42; 47; 50; 55; 55; 57; 59; 60; 61; 63. Do đó, \({Q_1} = \frac{{55 + 57}}{2} = 56\)
Tứ phân vị thứ ba là trung vị của dãy số liệu: 63; 67; 67; 68; 73; 75; 78; 79; 79; 101. Do đó, \({Q_3} = \frac{{73 + 75}}{2} = 74\).
Khoảng tứ phân vị là: \({\Delta _{{Q_1}}} = 74 - 56 = 18\)
Với mẫu số liệu ghép nhóm: Khoảng biến thiên là: \({R_2} = 110 - 40 = 70\)
Cỡ mẫu \(n = 20\). Giả sử \({x_1},{x_2},...,{x_{20}}\) là số thẻ vàng mà mỗi câu lạc bộ ngoại hạng Anh nhận được mùa giải 2021- 2022, các giá trị này đã được sắp xếp theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{{{x_5} + {x_6}}}{2}\) nên nhóm chứa tứ phân vị thứ nhất là nhóm \(\left[ {50;60} \right)\) và ta có: \(Q{'_1} = 50 + \frac{{\frac{{20}}{4} - 2}}{5}.10 = 56\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{{{x_{15}} + {x_{16}}}}{2}\) nên nhóm chứa tứ phân vị thứ ba là nhóm \(\left[ {70;80} \right)\) và ta có: \(Q{'_3} = 70 + \frac{{\frac{{3.20}}{4} - \left( {2 + 5 + 7} \right)}}{5}.10 = 72\)
Khoảng biến thiên của mẫu số liệu ghép nhóm là: \({\Delta _{{Q_2}}} = 72 - 56 = 16\)
Gía trị chính xác là \({R_1};\Delta {Q_1}\), giá trị xấp xỉ là \({R_2};\Delta {Q_2}\)
Bài tập 3.1 trang 78 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về đạo hàm, quy tắc tính đạo hàm và các ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài tập 3.1 yêu cầu học sinh xét hàm số f(x) = x3 - 3x2 + 2 và thực hiện các yêu cầu sau:
Để tính đạo hàm f'(x), ta sử dụng quy tắc tính đạo hàm của hàm số đa thức:
f'(x) = 3x2 - 6x
Để tìm các điểm cực trị của hàm số, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, phương trình có hai nghiệm: x = 0 và x = 2.
Để xác định xem các điểm này là điểm cực đại hay cực tiểu, ta xét dấu của đạo hàm bậc hai f''(x):
f''(x) = 6x - 6
Tại x = 0, f''(0) = -6 < 0, vậy x = 0 là điểm cực đại.
Tại x = 2, f''(2) = 6 > 0, vậy x = 2 là điểm cực tiểu.
Giá trị của hàm số tại các điểm cực trị là:
Vậy, hàm số có điểm cực đại là (0; 2) và điểm cực tiểu là (2; -2).
Để xác định khoảng đồng biến và nghịch biến của hàm số, ta xét dấu của đạo hàm f'(x):
Kết luận:
Bài tập 3.1 trang 78 SGK Toán 12 tập 1 - Kết nối tri thức có ứng dụng quan trọng trong việc giải quyết các bài toán thực tế liên quan đến tối ưu hóa, tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Ví dụ, trong kinh tế, bài toán tối ưu hóa lợi nhuận thường được giải quyết bằng cách tìm điểm cực trị của hàm số lợi nhuận. Trong vật lý, bài toán tìm quỹ đạo của vật thể chuyển động thường được giải quyết bằng cách tìm điểm cực trị của hàm số mô tả quỹ đạo.
Để nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm, học sinh nên luyện tập thêm các bài tập khác trong SGK Toán 12 tập 1 - Kết nối tri thức và các tài liệu tham khảo khác. Giaitoan.edu.vn cung cấp đầy đủ lời giải chi tiết các bài tập Toán 12, giúp các em học sinh học tập hiệu quả.