Bài tập 3.3 trang 79 SGK Toán 12 tập 1 thuộc chương trình học môn Toán lớp 12, sách Kết nối tri thức. Bài tập này thường xoay quanh các kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 3.3 trang 79, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Bảng sau đây cho biết chiều cao của các học sinh lớp 12A và 12B. a) Tìm khoảng biến thiên, khoảng tứ phân vị cho các mẫu số liệu ghép nhóm về chiều cao của học sinh lớp 12A, 12B. b) Để so sánh độ phân tán về chiều cao của học sinh hai lớp này ta nên dùng khoảng biến thiên hay khoảng tứ phân vị? Vì sao?
Đề bài
Bảng sau đây cho biết chiều cao của các học sinh lớp 12A và 12B.
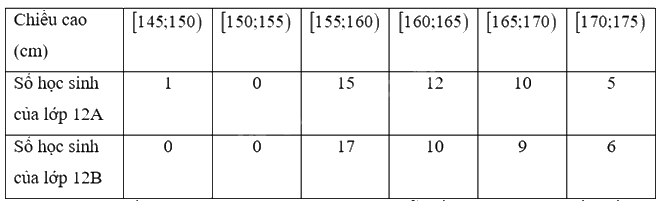a) Tìm khoảng biến thiên, khoảng tứ phân vị cho các mẫu số liệu ghép nhóm về chiều cao của học sinh lớp 12A, 12B.
b) Để so sánh độ phân tán về chiều cao của học sinh hai lớp này ta nên dùng khoảng biến thiên hay khoảng tứ phân vị? Vì sao?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về khoảng biến thiên của mẫu số liệu ghép nhóm để tính:
Cho mẫu số liệu ghép nhóm:
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: \(R = {a_{k + 1}} - {a_1}\).
Sử dụng kiến thức về khoảng tứ phân vị của mẫu số liệu ghép nhóm để tính: Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu là \({\Delta _Q}\), là hiệu số giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).
Sử dụng kiến thức về ý nghĩa của khoảng tứ phân vị để giải thích: Khoảng tứ phân vị của mẫu số liệu ghép nhóm chỉ phụ thuộc vào nửa giữa của mẫu số liệu, không bị ảnh hưởng bởi các giá trị bất thường.
Lời giải chi tiết
a) Lớp 12A: Khoảng biến thiên: \(R = 175 - 145 = 30\)
Ta có cỡ mẫu \(n = 43\). Giả sử \({x_1},{x_2},...,{x_{43}}\) là chiều cao của các học sinh lớp 12A và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.
Vì \(\frac{n}{4} = 10,75\) và \(1 < 10,75 < 1 + 15\) nên nhóm chứa tứ phân vị thứ nhất là nhóm \(\left[ {150;160} \right)\) và tứ phân vị thứ nhất là: \({Q_1} = 155 + \frac{{\frac{{43}}{4} - 1}}{{15}}.5 = 158,25\)
Vì \(\frac{{3n}}{4} = 32,25\) và \(1 + 15 + 12 < 32,25 < 1 + 15 + 12 + 10\) nên nhóm chứa tứ phân vị thứ ba là nhóm \(\left[ {165;170} \right)\) và tứ phân vị thứ ba là: \({Q_3} = 165 + \frac{{\frac{{3.43}}{4} - \left( {1 + 15 + 12} \right)}}{{10}}.5 = 167,125\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _{{Q_1}}} = 167,125 - 158,25 = 8,875\)
Lớp 12B: Khoảng biến thiên: \(R = 175 - 155 = 20\)
Ta có cỡ mẫu \(n = 42\). Giả sử \({x_1},{x_2},...,{x_{42}}\) là chiều cao của các học sinh lớp 12B và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.
Vì \(\frac{n}{4} = 10,5\) và \(0 < 10,5 < 17\) nên nhóm chứa tứ phân vị thứ nhất là nhóm \(\left[ {155;160} \right)\) và ta có: \(Q{'_1} = 155 + \frac{{\frac{{42}}{4} - 0}}{{17}}.5 = \frac{{5375}}{{34}}\)
Vì \(\frac{{3n}}{4} = 31,5\) và \(17 + 10 < 31,5 < 17 + 10 + 9\) nên nhóm chứa tứ phân vị thứ ba là nhóm \(\left[ {165;170} \right)\) và tứ phân vị thứ ba là: \(Q{'_3} = 165 + \frac{{\frac{{3.42}}{4} - \left( {17 + 10} \right)}}{9}.5 = \frac{{335}}{2}\)
Khoảng biến thiên của mẫu số liệu ghép nhóm là: \({\Delta _{{Q_2}}} = \frac{{335}}{2} - \frac{{5375}}{{34}} = \frac{{160}}{{17}}\)
b) Để so sánh độ phân tán về chiều cao của học sinh hai lớp này, ta nên dùng khoảng tứ phân vị vì khoảng tứ phân vị chỉ phụ thuộc vào nửa giữa của mẫu số liệu, không bị ảnh hưởng bởi các giá trị bất thường.
Bài tập 3.3 trang 79 SGK Toán 12 tập 1 - Kết nối tri thức là một phần quan trọng trong quá trình học tập môn Toán lớp 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế, từ đó củng cố và nâng cao hiểu biết về đạo hàm và ứng dụng của nó.
Bài tập 3.3 thường bao gồm các dạng bài sau:
Để giúp các em học sinh giải quyết bài tập 3.3 trang 79 SGK Toán 12 tập 1 một cách hiệu quả, Giaitoan.edu.vn xin trình bày lời giải chi tiết cho từng câu hỏi:
Cho hàm số y = x3 - 3x2 + 2. Hãy tính đạo hàm y' của hàm số.
Lời giải:
Áp dụng quy tắc đạo hàm của tổng và tích, ta có:
y' = 3x2 - 6x
Tìm khoảng đồng biến của hàm số y = x2 - 4x + 3.
Lời giải:
Tính đạo hàm y' = 2x - 4.
Giải bất phương trình y' > 0, ta được 2x - 4 > 0 ⇔ x > 2.
Vậy hàm số đồng biến trên khoảng (2; +∞).
Để giải các bài tập về đạo hàm một cách hiệu quả, các em học sinh cần:
Ngoài SGK Toán 12 tập 1 - Kết nối tri thức, các em học sinh có thể tham khảo thêm các tài liệu sau:
Bài tập 3.3 trang 79 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Hy vọng với lời giải chi tiết và các mẹo giải bài tập hiệu quả mà Giaitoan.edu.vn cung cấp, các em sẽ học tập tốt hơn và đạt kết quả cao trong môn Toán.
