Chào mừng các em học sinh đến với bài giải chi tiết mục 1 trang 50,51 SGK Toán 12 tập 2 chương trình Kết nối tri thức. Bài viết này cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập liên quan.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp các tài liệu học tập chất lượng và phương pháp giải bài tập hiệu quả.
CÔNG THỨC TÍNH GÓC GIỮA HAI ĐƯỜNG THẲNG
Trả lời câu hỏi Luyện tập 1 trang 51 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, tính góc giữa trục Oz và đường thẳng \(\Delta :\frac{{x - 3}}{1} = \frac{{y + 1}}{2} = \frac{{z - 1}}{{ - 2}}\).
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai đường thẳng để tính: Trong không gian Oxyz, cho hai đường thẳng \(\Delta \) và \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right),\overrightarrow {u'} = \left( {a';b';c'} \right)\). Khi đó: \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right| = \frac{{\left| {aa' + bb' + cc'} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} .\sqrt {a{'^2} + b{'^2} + c{'^2}} }}\).
Lời giải chi tiết:
Trục Oz có vectơ chỉ phương \(\overrightarrow k = \left( {0;0;1} \right)\), đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u \left( {1;2; - 2} \right)\). Do đó, \(\cos \left( {Oz,\Delta } \right) = \left| {\cos \left( {\overrightarrow k ,\overrightarrow u } \right)} \right| = \frac{{\left| {0.1 + 0.2 - 1.2} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} .\sqrt {{1^2} + {2^2} + {{\left( { - 2} \right)}^2}} }} = \frac{2}{3}\)
Suy ra: \(\left( {Oz,\Delta } \right) \approx 48,{2^o}\).
Trả lời câu hỏi Hoạt động 1 trang 50 SGK Toán 12 Kết nối tri thức
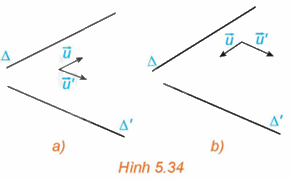
Trong không gian Oxyz, cho hai đường thẳng \(\Delta \) và \(\Delta '\) tương ứng có các vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right),\overrightarrow {u'} = \left( {a';b';c'} \right)\). (H.5.34).
a) Hãy tìm mối quan hệ giữa các góc \(\left( {\Delta ,\Delta '} \right)\) và \(\left( {\overrightarrow u ,\overrightarrow {u'} } \right)\).
b) Có nhận xét gì về mối quan hệ giữa \(\cos \left( {\Delta ,\Delta '} \right)\) và \(\left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right|\)?
Phương pháp giải:
Sử dụng kiến thức giá của vectơ để chứng minh: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ đó.
Lời giải chi tiết:
a) Vì \(\overrightarrow u \) và \(\overrightarrow {u'} \) lần lượt là các vectơ chỉ phương của hai đường thẳng \(\Delta \) và \(\Delta '\). Do đó, giá của \(\overrightarrow u \) song song với \(\Delta \), giá của \(\overrightarrow {u'} \) song song với \(\Delta '\). Do đó:
+) \(\left( {\Delta ,\Delta '} \right) = \left( {\overrightarrow u ,\overrightarrow {u'} } \right)\) nếu \(\left( {\overrightarrow u ,\overrightarrow {u'} } \right) \le {90^o}\)
+) \(\left( {\Delta ,\Delta '} \right) = {180^o} - \left( {\overrightarrow u ,\overrightarrow {u'} } \right)\) nếu \(\left( {\overrightarrow u ,\overrightarrow {u'} } \right) > {90^o}\)
b) Ta có: \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right|\).
Trả lời câu hỏi Hoạt động 1 trang 50 SGK Toán 12 Kết nối tri thức
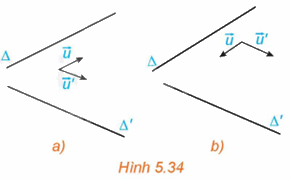
Trong không gian Oxyz, cho hai đường thẳng \(\Delta \) và \(\Delta '\) tương ứng có các vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right),\overrightarrow {u'} = \left( {a';b';c'} \right)\). (H.5.34).
a) Hãy tìm mối quan hệ giữa các góc \(\left( {\Delta ,\Delta '} \right)\) và \(\left( {\overrightarrow u ,\overrightarrow {u'} } \right)\).
b) Có nhận xét gì về mối quan hệ giữa \(\cos \left( {\Delta ,\Delta '} \right)\) và \(\left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right|\)?
Phương pháp giải:
Sử dụng kiến thức giá của vectơ để chứng minh: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ đó.
Lời giải chi tiết:
a) Vì \(\overrightarrow u \) và \(\overrightarrow {u'} \) lần lượt là các vectơ chỉ phương của hai đường thẳng \(\Delta \) và \(\Delta '\). Do đó, giá của \(\overrightarrow u \) song song với \(\Delta \), giá của \(\overrightarrow {u'} \) song song với \(\Delta '\). Do đó:
+) \(\left( {\Delta ,\Delta '} \right) = \left( {\overrightarrow u ,\overrightarrow {u'} } \right)\) nếu \(\left( {\overrightarrow u ,\overrightarrow {u'} } \right) \le {90^o}\)
+) \(\left( {\Delta ,\Delta '} \right) = {180^o} - \left( {\overrightarrow u ,\overrightarrow {u'} } \right)\) nếu \(\left( {\overrightarrow u ,\overrightarrow {u'} } \right) > {90^o}\)
b) Ta có: \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right|\).
Trả lời câu hỏi Luyện tập 1 trang 51 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, tính góc giữa trục Oz và đường thẳng \(\Delta :\frac{{x - 3}}{1} = \frac{{y + 1}}{2} = \frac{{z - 1}}{{ - 2}}\).
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai đường thẳng để tính: Trong không gian Oxyz, cho hai đường thẳng \(\Delta \) và \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right),\overrightarrow {u'} = \left( {a';b';c'} \right)\). Khi đó: \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right| = \frac{{\left| {aa' + bb' + cc'} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} .\sqrt {a{'^2} + b{'^2} + c{'^2}} }}\).
Lời giải chi tiết:
Trục Oz có vectơ chỉ phương \(\overrightarrow k = \left( {0;0;1} \right)\), đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u \left( {1;2; - 2} \right)\). Do đó, \(\cos \left( {Oz,\Delta } \right) = \left| {\cos \left( {\overrightarrow k ,\overrightarrow u } \right)} \right| = \frac{{\left| {0.1 + 0.2 - 1.2} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} .\sqrt {{1^2} + {2^2} + {{\left( { - 2} \right)}^2}} }} = \frac{2}{3}\)
Suy ra: \(\left( {Oz,\Delta } \right) \approx 48,{2^o}\).
Mục 1 trang 50,51 SGK Toán 12 tập 2 Kết nối tri thức tập trung vào việc ôn tập chương 3: Đạo hàm. Đây là một phần quan trọng trong chương trình Toán 12, đòi hỏi học sinh phải nắm vững các khái niệm, định lý và kỹ năng liên quan đến đạo hàm. Việc giải các bài tập trong SGK là một cách hiệu quả để củng cố kiến thức và rèn luyện kỹ năng giải toán.
Mục 1 bao gồm các bài tập trắc nghiệm và tự luận, yêu cầu học sinh vận dụng các kiến thức về:
Các bài tập trắc nghiệm trong mục này thường kiểm tra khả năng hiểu và vận dụng các khái niệm cơ bản về đạo hàm. Để giải các bài tập này, học sinh cần nắm vững định nghĩa đạo hàm, các quy tắc tính đạo hàm và các ứng dụng của đạo hàm.
Ví dụ:
Câu hỏi: Cho hàm số y = x3 - 3x2 + 2. Tính đạo hàm y' của hàm số.
Lời giải: y' = 3x2 - 6x
Các bài tập tự luận trong mục này thường yêu cầu học sinh trình bày lời giải chi tiết, rõ ràng và logic. Để giải các bài tập này, học sinh cần nắm vững các bước giải bài toán, sử dụng các công thức và định lý một cách chính xác.
Ví dụ:
Bài tập: Tìm cực trị của hàm số y = x3 - 3x2 + 2.
Lời giải:
Việc giải các bài tập trong Mục 1 trang 50,51 SGK Toán 12 tập 2 Kết nối tri thức là một bước quan trọng trong quá trình học tập môn Toán của các em. Hy vọng rằng với bài giải chi tiết và các mẹo giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong việc giải các bài tập và đạt kết quả tốt trong các kỳ thi.
| Hàm số y | Đạo hàm y' |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = u + v | y' = u' + v' |
| y = u.v | y' = u'v + uv' |
| y = u/v | y' = (u'v - uv')/v2 |