Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 23 và 24 sách giáo khoa Toán 12 tập 1 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
Đường tiệm cận xiên
Trả lời câu hỏi Luyện tập 3 trang 24 SGK Toán 12 Kết nối tri thức
Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 4x + 2}}{{1 - x}}\).
Phương pháp giải:
Sử dụng kiến thức về tìm khái niệm đường tiệm cận xiên để tìm tiệm cận xiên: Đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\).
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 4x + 2}}{{1 - x}} = + \infty \); \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 4x + 2}}{{1 - x}} = - \infty \)
Vậy tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\) là đường thẳng \(x = 1\)
Ta có: \(y = f\left( x \right) = \frac{{{x^2} - 4x + 2}}{{1 - x}} = - x + 3 - \frac{1}{{1 - x}}\)
Do đó, \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( { - x + 3} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 1}}{{1 - x}} = 0\), \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( { - x + 3} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - 1}}{{1 - x}} = 0\)
Vậy tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\) là đường thẳng \(y = - x + 3\)
Trả lời câu hỏi Hoạt động 3 trang 23 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = x - 1 + \frac{2}{{x + 1}}\) có đồ thị (C) và đường thẳng \(y = x - 1\) như Hình 1.24.
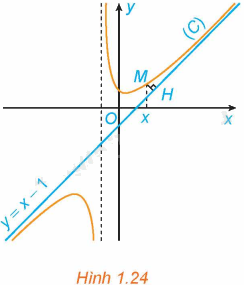
a) Với \(x > - 1\), xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng \(y = x - 1\). Có nhận xét gì về khoảng cách MH khi \(x \to + \infty \)?
b) Chứng tỏ rằng \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x - 1} \right)} \right] = 0\). Tính chất này thể hiện trên Hình 1.24 như thế nào?
Phương pháp giải:
Sử dụng kiến thức về giới hạn của hàm số để tính giới hạn.
Lời giải chi tiết:
a) Nhìn vào đồ thị ta thấy, khi \(x \to + \infty \) thì khoảng cách MH tiến tới 0.
b) Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left[ {x - 1 + \frac{2}{{x + 1}} - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{2}{{x + 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{2}{x}}}{{1 + \frac{1}{x}}} = 0\)
Tính chất này được thể hiện trong Hình 1.24 là: Khoảng cách từ điểm M của đồ thị hàm số (C) đến đường thẳng \(y = x - 1\) tiến đến 0 khi \(x \to + \infty \).
Trả lời câu hỏi Luyện tập 3 trang 24 SGK Toán 12 Kết nối tri thức
Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 4x + 2}}{{1 - x}}\).
Phương pháp giải:
Sử dụng kiến thức về tìm khái niệm đường tiệm cận xiên để tìm tiệm cận xiên: Đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\).
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 4x + 2}}{{1 - x}} = + \infty \); \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 4x + 2}}{{1 - x}} = - \infty \)
Vậy tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\) là đường thẳng \(x = 1\)
Ta có: \(y = f\left( x \right) = \frac{{{x^2} - 4x + 2}}{{1 - x}} = - x + 3 - \frac{1}{{1 - x}}\)
Do đó, \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( { - x + 3} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 1}}{{1 - x}} = 0\), \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( { - x + 3} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - 1}}{{1 - x}} = 0\)
Vậy tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\) là đường thẳng \(y = - x + 3\)
Trả lời câu hỏi Hoạt động 3 trang 23 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = x - 1 + \frac{2}{{x + 1}}\) có đồ thị (C) và đường thẳng \(y = x - 1\) như Hình 1.24.
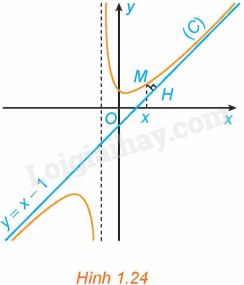
a) Với \(x > - 1\), xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng \(y = x - 1\). Có nhận xét gì về khoảng cách MH khi \(x \to + \infty \)?
b) Chứng tỏ rằng \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x - 1} \right)} \right] = 0\). Tính chất này thể hiện trên Hình 1.24 như thế nào?
Phương pháp giải:
Sử dụng kiến thức về giới hạn của hàm số để tính giới hạn.
Lời giải chi tiết:
a) Nhìn vào đồ thị ta thấy, khi \(x \to + \infty \) thì khoảng cách MH tiến tới 0.
b) Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left[ {x - 1 + \frac{2}{{x + 1}} - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{2}{{x + 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{2}{x}}}{{1 + \frac{1}{x}}} = 0\)
Tính chất này được thể hiện trong Hình 1.24 là: Khoảng cách từ điểm M của đồ thị hàm số (C) đến đường thẳng \(y = x - 1\) tiến đến 0 khi \(x \to + \infty \).
Mục 3 trong SGK Toán 12 tập 1 - Kết nối tri thức tập trung vào việc nghiên cứu về giới hạn của hàm số tại một điểm và giới hạn vô cùng. Đây là một trong những khái niệm nền tảng quan trọng trong chương trình Toán học lớp 12, đóng vai trò then chốt trong việc hiểu và giải quyết các bài toán về đạo hàm, tích phân và các ứng dụng của chúng.
Mục 3 bao gồm các nội dung chính sau:
Dưới đây là lời giải chi tiết cho các bài tập trang 23 SGK Toán 12 tập 1 - Kết nối tri thức:
Tiếp theo, chúng ta sẽ cùng giải chi tiết các bài tập trang 24 SGK Toán 12 tập 1 - Kết nối tri thức:
Để giải tốt các bài tập về giới hạn, các em cần lưu ý những điều sau:
Giới hạn có nhiều ứng dụng quan trọng trong Toán học và các lĩnh vực khác. Ví dụ, giới hạn được sử dụng để tính đạo hàm của hàm số tại một điểm, để tính tích phân của hàm số trên một khoảng, và để giải các bài toán về sự hội tụ của dãy số và chuỗi số.
Hy vọng rằng với lời giải chi tiết và những lưu ý trên, các em học sinh đã hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 3 trang 23, 24 SGK Toán 12 tập 1 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Bài tập | Trang | Độ khó |
|---|---|---|
| Bài 1 | 23 | Dễ |
| Bài 2 | 23 | Trung bình |
| Bài 3 | 23 | Khó |
| Bài 4 | 24 | Dễ |
| Bài 5 | 24 | Trung bình |
| Bài 6 | 24 | Khó |