Bài tập 2.17 trang 65 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Kết nối tri thức. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 2.17, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
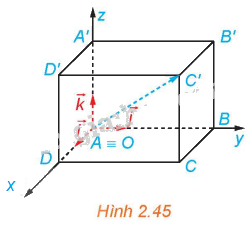
Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O và các đỉnh D, B, A’ có tọa độ lần lượt là (2; 0; 0), (0; 4; 0), (0; 0; 3) (H.2.45). Xác định tọa độ của các đỉnh còn lại của hình hộp chữ nhật.
Đề bài
Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O và các đỉnh D, B, A’ có tọa độ lần lượt là (2; 0; 0), (0; 4; 0), (0; 0; 3) (H.2.45). Xác định tọa độ của các đỉnh còn lại của hình hộp chữ nhật.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tọa độ của điểm trong không gian để xác định tọa độ các điểm: Trong không gian Oxyz, cho một điểm M tùy ý. Bộ ba số (x; y; z) duy nhất sao cho \(\overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \) được gọi là tọa độ của điểm M đối với hệ tọa độ Oxyz. Khi đó, ta viết \(M = \left( {x;y;z} \right)\) hoặc \(M\left( {x;y;z} \right)\), trong đó x là hoành độ, y là tung độ, z là cao độ của M.
Lời giải chi tiết
Vì A trùng gốc O nên A(0; 0; 0).
Vì D thuộc tia Ox nên hai vectơ \(\overrightarrow {OD} \) và \(\overrightarrow i \) cùng hướng. Do đó, tồn tại số thực m sao cho \(\overrightarrow {OD} = m\overrightarrow i \). Mà D(2; 0; 0) nên \(m = 2\).
Vì B thuộc tia Oy nên hai vectơ \(\overrightarrow {OB} \) và \(\overrightarrow j \) cùng hướng. Do đó, tồn tại số thực n sao cho \(\overrightarrow {OB} = n\overrightarrow j \). Mà B(0; 4; 0) nên \(n = 4\)
Vì A’ thuộc tia Oz nên hai vectơ \(\overrightarrow {OA'} \) và \(\overrightarrow k \) cùng hướng. Do đó, tồn tại số thực p sao cho \(\overrightarrow {OA'} = p\overrightarrow k \). Mà A’(0; 0; 3) nên \(p = 3\).
Vì ODCB là hình bình hành nên \(\overrightarrow {OC} = \overrightarrow {OD} + \overrightarrow {OB} = m\overrightarrow i + n\overrightarrow j = 2\overrightarrow i + 4\overrightarrow j \). Do đó, C(2; 4; 0).
Vì OA’B’B là hình bình hành nên \(\overrightarrow {OB'} = \overrightarrow {OA'} + \overrightarrow {OB} = p\overrightarrow k + n\overrightarrow j = 3\overrightarrow k + 4\overrightarrow j \). Do đó, B’(0; 4; 3).
Vì OA’D’D là hình bình hành nên \(\overrightarrow {OD'} = \overrightarrow {OA'} + \overrightarrow {OD} = m\overrightarrow i + p\overrightarrow k = 2\overrightarrow i + 3\overrightarrow k \). Do đó, D’(2; 0; 3).
Vì ABCD. A’B’C’D’ là hình hộp chữ nhật nên theo quy tắc hình hộp ta có:
\(\overrightarrow {OC'} = \overrightarrow {OD} + \overrightarrow {OB} + \overrightarrow {OA'} = m\overrightarrow i + n\overrightarrow j + p\overrightarrow k = 2\overrightarrow i + 4\overrightarrow j + 3\overrightarrow k \). Do đó, C’(2; 4; 3).
Bài tập 2.17 trang 65 SGK Toán 12 tập 1 - Kết nối tri thức là một bài toán quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Bài toán này thường liên quan đến việc tìm đạo hàm của hàm số, xét dấu đạo hàm để xác định tính đơn điệu của hàm số, và tìm cực trị của hàm số.
Để hiểu rõ hơn về bài tập này, chúng ta cần xem xét nội dung cụ thể của bài tập. Bài tập 2.17 thường yêu cầu học sinh thực hiện các bước sau:
Dưới đây là lời giải chi tiết bài tập 2.17 trang 65 SGK Toán 12 tập 1 - Kết nối tri thức. (Lưu ý: Vì nội dung bài tập cụ thể không được cung cấp, phần này sẽ trình bày một ví dụ minh họa về cách giải một bài toán tương tự.)
Giả sử hàm số cần xét là: f(x) = x3 - 3x2 + 2
f'(x) = 3x2 - 6x
f'(x) = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy, f'(x) = 0 khi x = 0 hoặc x = 2.
Xét dấu f'(x) trên các khoảng:
Tại x = 0, f'(x) đổi dấu từ dương sang âm, nên x = 0 là điểm cực đại. Giá trị cực đại là f(0) = 2.
Tại x = 2, f'(x) đổi dấu từ âm sang dương, nên x = 2 là điểm cực tiểu. Giá trị cực tiểu là f(2) = -2.
Đạo hàm là một công cụ mạnh mẽ trong việc giải quyết các bài toán liên quan đến hàm số. Việc hiểu rõ các khái niệm về đạo hàm, tính đơn điệu, cực trị của hàm số sẽ giúp học sinh giải quyết các bài tập một cách hiệu quả và chính xác.
Bài tập 2.17 trang 65 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và các mẹo học tập trên, các em học sinh sẽ tự tin hơn trong việc giải quyết bài tập này và đạt kết quả tốt trong môn Toán.