Chương trình Toán 12 Kết nối tri thức tập trung vào việc ứng dụng tích phân để giải quyết các bài toán thực tế trong hình học. Đây là một phần quan trọng giúp học sinh hiểu sâu sắc hơn về mối liên hệ giữa đại số và hình học.
Tại giaitoan.edu.vn, chúng tôi cung cấp đầy đủ lý thuyết, ví dụ minh họa và bài tập thực hành để bạn có thể nắm vững kiến thức này một cách hiệu quả.
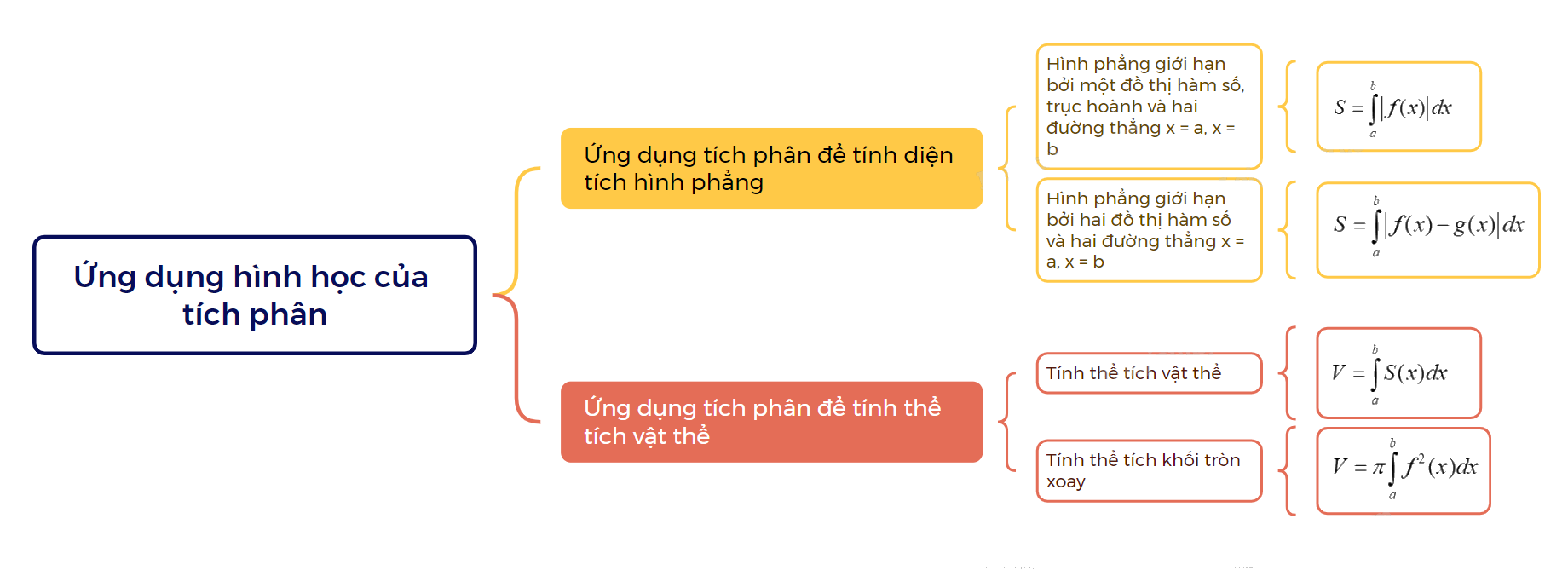
1.Ứng dụng tích phân để tính diện tích hình phẳng a) Hình phẳng giới hạn bởi một đồ thị hàm số, trục hoành và hai đường thẳng x = a, x = b
1.Ứng dụng tích phân để tính diện tích hình phẳng
a) Hình phẳng giới hạn bởi một đồ thị hàm số, trục hoành và hai đường thẳng x = a, x = b
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x) liên tục, trục hoành và hai đường thẳng x = a, x = b (a < b) được tính bằng công thức \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \) |
b) Hình phẳng giới hạn bởi hai đồ thị hàm số và hai đường thẳng x = a, x = b
Diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số y = f(x), g(x) liên tục trên \(\left[ {a;b} \right]\) và hai đường thẳng x = a, x = b được tính bằng công thức \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \) |
2. Ứng dụng tích phân để tính thể tích vật thể
a) Tính thể tích vật thể
Cho một vật thể trong không gian Oxyz. Gọi \(\beta \) là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm có hoành độ x = a, x = b. Một mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x cắt vật thể theo mặt cắt có diện tích là S(x). Giả sử S(x) là hàm số liên tục trên đoạn \(\left[ {a;b} \right]\). Khi đó thể tích V của vật thể \(\beta \) được tính bởi công thức \(V = \int\limits_a^b {S(x)dx} \) |
b) Tính thể tích khối tròn xoay
Cho hàm số f(x) liên tục, không âm trên đoạn \(\left[ {a;b} \right]\). Khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b xung quanh trục hoành, ta được hình khối gọi là một khối tròn xoay. Khi cắt khối tròn xoay đó bởi một mặt phẳng vuông góc với trục Ox tại điểm \(x \in \left[ {a;b} \right]\) được một hình tròn có bán kính f(x). Thể tích của khối tròn xoay này là \(V = \pi \int\limits_a^b {{f^2}(x)dx} \)\(\) |
Ứng dụng của tích phân trong hình học là một phần quan trọng của chương trình Toán 12 Kết nối tri thức. Nó cho phép chúng ta tính toán diện tích các hình phẳng và thể tích các khối tròn xoay một cách chính xác và hiệu quả. Dưới đây là tổng hợp lý thuyết chi tiết và các ví dụ minh họa.
Để tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành Ox và hai đường thẳng x = a, x = b (với a < b), ta sử dụng công thức:
S = ∫ab |f(x)| dx
Trong đó:
Ví dụ 1: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x2, trục hoành Ox và hai đường thẳng x = -1, x = 2.
Giải:
Diện tích hình phẳng cần tính là:
S = ∫-12 |x2| dx = ∫-12 x2 dx = [x3/3]-12 = (8/3) - (-1/3) = 3
Có hai phương pháp chính để tính thể tích khối tròn xoay:
1. Phương pháp đĩa:
Nếu quay miền phẳng giới hạn bởi y = f(x), trục Ox, x = a, x = b quanh trục Ox, thể tích khối tròn xoay được tính bằng:
V = π ∫ab [f(x)]2 dx
Ví dụ 2: Tính thể tích khối tròn xoay tạo thành khi quay miền phẳng giới hạn bởi y = √x, trục Ox và x = 4 quanh trục Ox.
Giải:
Thể tích khối tròn xoay cần tính là:
V = π ∫04 (√x)2 dx = π ∫04 x dx = π [x2/2]04 = π (16/2) = 8π
2. Phương pháp vỏ:
Nếu quay miền phẳng giới hạn bởi x = g(y), trục Oy, y = c, y = d quanh trục Oy, thể tích khối tròn xoay được tính bằng:
V = π ∫cd [g(y)]2 dy
Các bài tập ứng dụng tích phân trong hình học thường xoay quanh việc:
Hy vọng với những kiến thức và ví dụ trên, bạn đã có cái nhìn tổng quan về lý thuyết Ứng dụng hình học của tích phân Toán 12 Kết nối tri thức. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức này nhé!