Giải bài tập 6.9 trang 78 SGK Toán 12 tập 2 - Kết nối tri thức

Bài tập 6.9 trang 78 SGK Toán 12 tập 2 thuộc chương trình Toán 12 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến tính đơn điệu của hàm số. Bài tập này thường gặp trong các kỳ thi THPT Quốc gia, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 6.9 trang 78 SGK Toán 12 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán.

Tại nhà máy X sản xuất linh kiện điện tử tỉ lệ sản phẩm đạt tiêu chuẩn là 80%. Trước khi xuất xưởng ra thị trường, các linh kiện điện tử đều phải trải qua khâu kiểm tra chất lượng để đóng dấu OTK. Vì sự kiểm tra không tuyệt đối hoàn hảo nên nếu một linh kiện điện tử đạt tiêu chuẩn thì nó có xác suất 0,99 được đóng dấu OTK; nếu một linh kiện điện tử không đạt tiêu chuẩn thì nó có xác suất 0,95 không được đóng dấu OTK. Chọn ngẫu nhiên một linh kiện điện tử của nhà máy X trên thị trường. a) Tính x

Đề bài

a) Tính xác suất để linh kiện điện tử đó được đóng dấu OTK.

b) Dùng sơ đồ hình cây, hãy mô tả cách tính xác suất để linh kiện điện tử được chọn không được đóng dấu OTK.

Phương pháp giải - Xem chi tiết Giải bài tập 6.9 trang 78 SGK Toán 12 tập 2 - Kết nối tri thức 1

Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B. Khi đó, ta có công thức sau: \(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\overline A } \right).P\left( {B|\overline A } \right)\).

Lời giải chi tiết

Gọi A là biến cố: “Linh kiện điện tử đạt tiêu chuẩn”, B là biến cố: “linh kiện được đóng dấu OTK”.

Ta có: \(P\left( A \right) = 0,8 \Rightarrow P\left( {\overline A } \right) = 0,2\), \(P\left( {B|A} \right) = 0,99,P\left( {\overline B |\overline A } \right) = 0,95\)

Ta có: \(P\left( {B|\overline A } \right) = 1 - 0,95 = 0,05\)

a) Xác suất để linh kiện được đóng dấu OTK là:

\(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\overline A } \right).P\left( {B|\overline A } \right) = 0,8.0,99 + 0,2.0,05 = 0,802\)

b) Ta có sơ đồ hình cây:

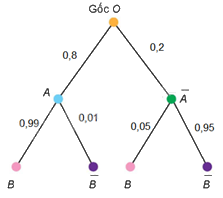
Giải bài tập 6.9 trang 78 SGK Toán 12 tập 2 - Kết nối tri thức 2

Trên nhánh OA và \(O\overline A \) tương ứng ghi P(A) và \(P\left( {\overline A } \right)\);

Trên nhánh AB và \(A\overline B \) tương ứng ghi \(P\left( {B|A} \right)\) và \(P\left( {\overline B |A} \right)\);

Trên nhánh \(\overline A B\) và \(\overline {AB} \) tương ứng ghi \(P\left( {B|\overline A } \right)\) và \(P\left( {\overline B |\overline A } \right)\).

Có hai nhánh cây đi tới \(\overline B \) là \[OA\overline B \] và \(O\overline A \overline B \)

Do đó, \(P\left( {\overline B } \right) = 0,8.0,01 + 0,95.0,2 = 0,198\)

Vậy xác suất để linh kiện điện tử được chọn không được đóng dấu OTK là 0,198.

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 6.9 trang 78 SGK Toán 12 tập 2 - Kết nối tri thức đặc sắc thuộc chuyên mục đề toán 12 trên nền tảng học toán. Với bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 6.9 trang 78 SGK Toán 12 tập 2 - Kết nối tri thức: Hướng dẫn chi tiết

Bài tập 6.9 SGK Toán 12 tập 2 Kết nối tri thức yêu cầu xét tính đơn điệu của hàm số. Để giải bài tập này, chúng ta cần thực hiện các bước sau:

Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
Tính đạo hàm của hàm số: Sử dụng các quy tắc tính đạo hàm để tìm đạo hàm f'(x).
Tìm các điểm tới hạn: Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng 0.
Xét dấu đạo hàm: Lập bảng xét dấu đạo hàm trên các khoảng xác định bởi các điểm tới hạn.
Kết luận về tính đơn điệu: Dựa vào dấu của đạo hàm để kết luận hàm số đồng biến hay nghịch biến trên các khoảng tương ứng.

Ví dụ minh họa:

Giả sử hàm số f(x) = x³ - 3x² + 2. Ta thực hiện các bước sau:

Tập xác định: D = ℝ
Đạo hàm: f'(x) = 3x² - 6x
Điểm tới hạn: 3x² - 6x = 0 => x = 0 hoặc x = 2
Bảng xét dấu:

Khoảng	x	-∞	0	2	+∞
f'(x)	+	-	+
f(x)	Đồng biến	Nghịch biến	Đồng biến

Kết luận: Hàm số f(x) đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).

Lưu ý quan trọng:

Khi xét dấu đạo hàm, cần chú ý đến các điểm không xác định của đạo hàm. Ngoài ra, cần kiểm tra lại kết quả bằng cách vẽ đồ thị hàm số hoặc sử dụng các công cụ tính toán trực tuyến.

Bài tập 6.9 trang 78 SGK Toán 12 tập 2 thường có nhiều dạng khác nhau, đòi hỏi học sinh phải nắm vững kiến thức về đạo hàm và các phương pháp giải toán liên quan. Việc luyện tập thường xuyên và tìm hiểu các ví dụ minh họa sẽ giúp các em học sinh giải quyết các bài toán này một cách hiệu quả.

Ngoài ra, các em có thể tham khảo thêm các tài liệu học tập khác như sách bài tập, đề thi thử, và các trang web học toán online để nâng cao kiến thức và kỹ năng giải toán.

Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục môn Toán. Chúng tôi hy vọng rằng lời giải chi tiết bài tập 6.9 trang 78 SGK Toán 12 tập 2 này sẽ giúp các em học sinh hiểu rõ hơn về kiến thức và phương pháp giải toán.

Để hiểu sâu hơn về các khái niệm liên quan đến tính đơn điệu của hàm số, các em có thể tìm hiểu thêm về:

Đạo hàm: Định nghĩa, ý nghĩa, các quy tắc tính đạo hàm.
Điểm cực trị: Điểm cực đại, điểm cực tiểu, điều kiện để hàm số có cực trị.
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số: Phương pháp tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một khoảng.

Việc nắm vững các khái niệm này sẽ giúp các em giải quyết các bài toán về tính đơn điệu của hàm số một cách dễ dàng và hiệu quả hơn.

Chúc các em học tập tốt và đạt kết quả cao trong các kỳ thi!