Giải bài tập 2.7 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức

Bài tập 2.7 trang 58 SGK Toán 12 tập 1 thuộc chương trình học môn Toán lớp 12, sách Kết nối tri thức. Bài tập này thường xoay quanh các kiến thức về đạo hàm, ứng dụng đạo hàm để khảo sát hàm số.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

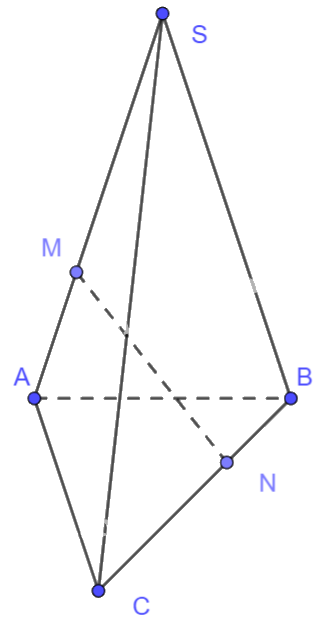
Cho hình chóp S.ABC. Trên cạnh SA, lấy điểm M sao cho \(SM = 2AM\). Trên cạnh BC, lấy điểm N sao cho \(CN = 2BN\). Chứng minh rằng \(\overrightarrow {MN} = \frac{1}{3}\left( {\overrightarrow {SA} + \overrightarrow {BC} } \right) + \overrightarrow {AB} \).

Đề bài

Phương pháp giải - Xem chi tiết Giải bài tập 2.7 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức 1

Sử dụng kiến thức về quy tắc ba điểm để chứng minh: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)

Sử dụng kiến thức về khái niệm tích của một số với một vectơ trong không gian để chứng minh: Trong không gian, tích của một số thực \(k \ne 0\) với một vectơ \(\overrightarrow a \ne \overrightarrow 0 \) là một vectơ, kí hiệu là \(k\overrightarrow a \) được xác định như sau:

- Cùng hướng với vectơ \(\overrightarrow a \) nếu \(k > 0\), ngược hướng với vectơ \(\overrightarrow a \) nếu \(k < 0\).

- Có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\).

Lời giải chi tiết

Ta có: \(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AC} + \overrightarrow {CN} = \frac{1}{3}\overrightarrow {SA} + \overrightarrow {AB} + \overrightarrow {BC} + \frac{2}{3}\overrightarrow {CB} \)

\( = \frac{1}{3}\overrightarrow {SA} + \overrightarrow {BC} - \frac{2}{3}\overrightarrow {BC} + \overrightarrow {AB} = \frac{1}{3}\left( {\overrightarrow {SA} + \overrightarrow {BC} } \right) + \overrightarrow {AB} \) (đpcm)

Giải bài tập 2.7 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức 2

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 2.7 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức đặc sắc thuộc chuyên mục giải bài tập toán 12 trên nền tảng tài liệu toán. Với bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 2.7 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức: Tổng quan

Bài tập 2.7 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán lớp 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và định lý liên quan đến đạo hàm, đồng thời rèn luyện kỹ năng giải toán một cách thành thạo.

Nội dung bài tập 2.7 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức

Bài tập 2.7 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức thường bao gồm các dạng bài sau:

Dạng 1: Tìm đạo hàm của hàm số.
Dạng 2: Khảo sát hàm số bằng đạo hàm (xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn).
Dạng 3: Giải các bài toán tối ưu hóa (tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số).
Dạng 4: Ứng dụng đạo hàm để giải các bài toán thực tế.

Lời giải chi tiết bài tập 2.7 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức

Để giúp các em học sinh giải bài tập 2.7 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức một cách dễ dàng, Giaitoan.edu.vn xin trình bày lời giải chi tiết cho từng dạng bài:

Dạng 1: Tìm đạo hàm của hàm số

Để tìm đạo hàm của hàm số, học sinh cần áp dụng các quy tắc tính đạo hàm cơ bản, bao gồm:

Quy tắc đạo hàm của tổng, hiệu, tích, thương của các hàm số.
Quy tắc đạo hàm của hàm hợp.
Đạo hàm của các hàm số lượng giác, hàm mũ, hàm logarit.

Ví dụ: Tìm đạo hàm của hàm số y = x² + 2x + 1.

Lời giải: y' = 2x + 2.

Dạng 2: Khảo sát hàm số bằng đạo hàm

Để khảo sát hàm số bằng đạo hàm, học sinh cần thực hiện các bước sau:

Tính đạo hàm cấp nhất y'.
Tìm các điểm cực trị của hàm số bằng cách giải phương trình y' = 0.
Xác định khoảng đồng biến, nghịch biến của hàm số dựa vào dấu của y'.
Tính đạo hàm cấp hai y''.
Tìm các điểm uốn của hàm số bằng cách giải phương trình y'' = 0.
Xác định khoảng lồi, lõm của hàm số dựa vào dấu của y''.

Ví dụ: Khảo sát hàm số y = x³ - 3x² + 2.

Lời giải:

y' = 3x² - 6x.
y' = 0 ⇔ x = 0 hoặc x = 2.
Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
y'' = 6x - 6.
y'' = 0 ⇔ x = 1.
Hàm số lõm trên khoảng (-∞; 1), lồi trên khoảng (1; +∞).

Dạng 3: Giải các bài toán tối ưu hóa

Để giải các bài toán tối ưu hóa, học sinh cần thực hiện các bước sau:

Xây dựng hàm số biểu diễn đại lượng cần tìm.
Tìm tập xác định của hàm số.
Tính đạo hàm của hàm số.
Tìm các điểm cực trị của hàm số.
So sánh các giá trị của hàm số tại các điểm cực trị và các điểm biên của tập xác định để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số.

Dạng 4: Ứng dụng đạo hàm để giải các bài toán thực tế

Các bài toán thực tế thường liên quan đến các vấn đề về tối ưu hóa, chẳng hạn như tìm kích thước tối ưu của một vật thể để đạt được diện tích lớn nhất hoặc thể tích nhỏ nhất. Để giải các bài toán này, học sinh cần vận dụng kiến thức về đạo hàm để xây dựng hàm số biểu diễn đại lượng cần tìm và tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số.

Lưu ý khi giải bài tập 2.7 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức

Nắm vững các khái niệm và định lý liên quan đến đạo hàm.
Rèn luyện kỹ năng giải toán một cách thành thạo.
Đọc kỹ đề bài và xác định đúng yêu cầu của bài toán.
Kiểm tra lại kết quả sau khi giải xong bài toán.

Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ giải bài tập 2.7 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức một cách dễ dàng và hiệu quả. Chúc các em học tốt!