Lý thuyết Giá trị lớn nhất - nhỏ nhất hàm số Toán 12 Kết nối tri thức

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Kết nối tri thức

Đây là một trong những chủ đề quan trọng của chương trình Toán 12, giúp học sinh hiểu rõ về tính chất của hàm số và ứng dụng trong giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp đầy đủ lý thuyết, ví dụ minh họa và bài tập thực hành để bạn nắm vững kiến thức này.

Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn trải nghiệm học toán online tốt nhất với nội dung được trình bày rõ ràng, dễ hiểu và cập nhật theo chương trình Kết nối tri thức.

1. Định nghĩa Khái niệm GTLN, GTNN của hàm số

1. Định nghĩa

Khái niệm GTLN, GTNN của hàm số

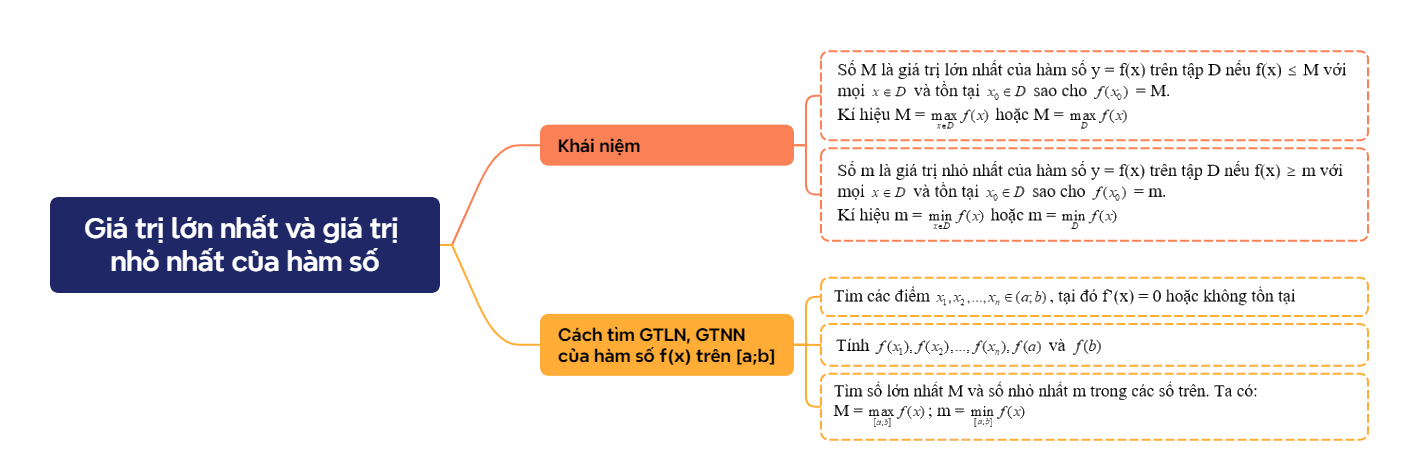
Cho hàm số y = f(x) xác định trên tập D.

- Số M là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu f(x) $ \le $ M với mọi $x \in D$ và tồn tại ${x_0} \in D$ sao cho $f({x_0})$ = M.

Kí hiệu M = $\mathop {\max }\limits_{x \in D} f(x)$ hoặc M = $\underset{D}{\mathop{\max }}\,f(x)$

- Số m là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu f(x) $ \ge $ m với mọi $x \in D$ và tồn tại ${x_0} \in D$ sao cho $f({x_0})$ = m.

Kí hiệu m = $\mathop {\min }\limits_{x \in D} f(x)$ hoặc m = $\mathop {\min }\limits_D f(x)$

Ví dụ: Tìm GTLN, GTNN của hàm số $y = f(x) = \sqrt {1 - {x^2}} $

Tập xác định của hàm số là $\left[ { - 1;1} \right]$

Ta có:

$f(x) = \sqrt {1 - {x^2}} $ $ \ge $ 0; dấu bằng xảy ra khi $1 - {x^2} = 0$, tức x = -1 hoặc x = 1.

Do đó $\mathop {\min }\limits_{x \in \left[ { - 1;1} \right]} f(x) = f( - 1) = f(1) = 0$

$f(x) = \sqrt {1 - {x^2}} $ $ \le 1$; dấu bằng xảy ra khi $1 - {x^2} = 1$, tức x = 0.

Do đó $\mathop {\max }\limits_{x \in \left[ { - 1;1} \right]} f(x) = f(0) = 1$

2. Cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn

Giả sử y = f(x) là hàm số liên tục trên $\left[ {a;b} \right]$ và có đạo hàm trên (a;b), có thể trừ ra tại một số hữu hạn điểm mà tại đó hàm số không có đạo hàm. Giả sử chỉ có hữu hạn điểm trong đoạn $\left[ {a;b} \right]$ mà đạo hàm f’(x) = 0.

Các bước tìm GTLN và GTNN của hàm số f(x) trên đoạn $\left[ {a;b} \right]$:

Tìm các điểm ${x_1},{x_2},...,{x_n} \in (a;b)$, tại đó f’(x) = 0 hoặc không tồn tại
Tính $f({x_1}),f({x_2}),...,f({x_n}),f(a)$ và $f(b)$
Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:

M = $\mathop {\max }\limits_{\left[ {a;b} \right]} f(x)$; m = $\mathop {\min }\limits_{\left[ {a;b} \right]} f(x)$

Ví dụ: Tìm GTLN và GTNN của hàm số $y = {x^4} - 4{x^2} + 3$ trên đoạn $\left[ {0;4} \right]$

Ta có: $y' = 4{x^3} - 8x = 4x({x^2} - 2);y' = 0 \Leftrightarrow x = 0$ hoặc $x = \sqrt 2 $ (vì $x \in \left[ {0;4} \right]$)

y(0) = 3; y(4) = 195; y($\sqrt 2 $) = -1

Do đó: $\mathop {\max }\limits_{\left[ {0;4} \right]} y = y(4) = 195$; $\mathop {\min }\limits_{\left[ {0;4} \right]} y = y(\sqrt 2 ) = - 1$

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Kết nối tri thức 1

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Kết nối tri thức đặc sắc thuộc chuyên mục bài tập toán 12 trên nền tảng toán math. Với bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Kết nối tri thức

Trong chương trình Toán 12, việc nắm vững lý thuyết về giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số là vô cùng quan trọng. Nó không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng cho việc ứng dụng vào các lĩnh vực khác.

1. Khái niệm về Giá trị lớn nhất và Giá trị nhỏ nhất của hàm số

Cho hàm số f(x) xác định trên tập D. Số M được gọi là giá trị lớn nhất của hàm số f(x) trên D nếu f(x) ≤ M với mọi x thuộc D và tồn tại ít nhất một x₀ thuộc D sao cho f(x₀) = M. Số m được gọi là giá trị nhỏ nhất của hàm số f(x) trên D nếu f(x) ≥ m với mọi x thuộc D và tồn tại ít nhất một x₀ thuộc D sao cho f(x₀) = m.

2. Điều kiện để hàm số đạt GTLN, GTNN trên một khoảng hoặc đoạn

Để tìm GTLN và GTNN của hàm số f(x) trên một khoảng hoặc đoạn, ta thường thực hiện các bước sau:

Tính đạo hàm f'(x) của hàm số.
Tìm các điểm dừng (điểm mà f'(x) = 0) và các điểm không xác định đạo hàm.
Tính giá trị của hàm số tại các điểm dừng, điểm không xác định đạo hàm và các mút của khoảng hoặc đoạn.
So sánh các giá trị này để tìm ra GTLN và GTNN.

3. Các dạng bài tập thường gặp

Tìm GTLN, GTNN của hàm số trên một đoạn: Đây là dạng bài tập cơ bản, yêu cầu học sinh áp dụng các bước đã nêu ở trên.
Tìm GTLN, GTNN của hàm số trên một khoảng: Trong trường hợp này, cần xét giới hạn của hàm số khi x tiến tới các mút của khoảng.
Tìm GTLN, GTNN của hàm số có điều kiện: Dạng bài tập này thường yêu cầu sử dụng phương pháp thế hoặc phương pháp nhân tử Lagrange.

4. Ví dụ minh họa

Ví dụ 1: Tìm GTLN và GTNN của hàm số f(x) = x² - 4x + 3 trên đoạn [0; 3].

Giải:

f'(x) = 2x - 4
f'(x) = 0 ⇔ x = 2
Tính giá trị của hàm số tại các điểm x = 0, x = 2, x = 3:

f(0) = 3
f(2) = -1
f(3) = 0

So sánh các giá trị, ta thấy GTLN của hàm số trên đoạn [0; 3] là 3 tại x = 0 và GTNN là -1 tại x = 2.

5. Lưu ý quan trọng

Khi tìm GTLN và GTNN của hàm số, cần chú ý đến tập xác định của hàm số và các điểm không xác định đạo hàm. Ngoài ra, cần kiểm tra kỹ các điều kiện để đảm bảo kết quả tìm được là chính xác.

6. Bài tập thực hành

Để củng cố kiến thức, bạn có thể thực hành giải các bài tập sau:

Tìm GTLN và GTNN của hàm số f(x) = -x² + 6x - 5 trên đoạn [1; 4].
Tìm GTLN và GTNN của hàm số f(x) = x³ - 3x² + 2 trên khoảng (-1; 1).

Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Kết nối tri thức. Chúc bạn học tập tốt!