Chào mừng bạn đến với bài học về Lý thuyết Phương sai và Độ lệch chuẩn trong chương trình Toán 12 Kết nối tri thức. Đây là một phần kiến thức quan trọng trong chương trình thống kê, giúp bạn hiểu rõ hơn về mức độ phân tán của dữ liệu.
Bài học này sẽ cung cấp cho bạn những khái niệm cơ bản, công thức tính toán và các ví dụ minh họa để bạn có thể áp dụng vào giải các bài tập thực tế.
1. Phương sai và độ lệch chuẩn
1. Phương sai và độ lệch chuẩn
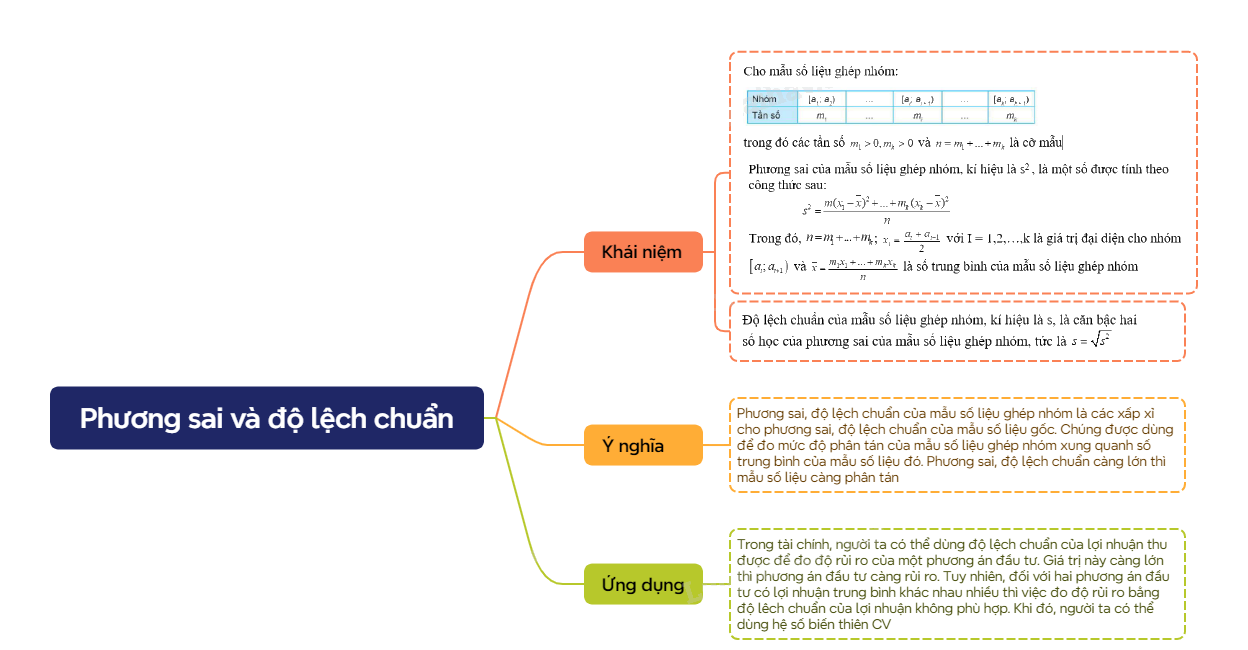
Cho mẫu số liệu ghép nhóm:

trong đó các tần số \({m_1} > 0,{m_k} > 0\) và \(n = {m_1} + ... + {m_k}\) là cỡ mẫu
Phương sai của mẫu số liệu ghép nhóm, kí hiệu là s2 , là một số được tính theo công thức sau: \[{s^2} = \frac{{m{{({x_1} - \overline x )}^2} + ... + {m_k}{{({x_k} - \overline x )}^2}}}{n}\] Trong đó, \(n = {m_1} + ... + {m_k}\); \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) với I = 1,2,…,k là giá trị đại diện cho nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\) và \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm. Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \). |
Ý nghĩa: Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm là các xấp xỉ cho phương sai, độ lệch chuẩn của mẫu số liệu gốc. Chúng được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu đó. Phương sai, độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán
2. Sử dụng phương sai, độ lệch chuẩn đo độ rủi ro
Ví dụ: Anh An đầu tư số tiền bằng nhau vào hai lĩnh vực kinh doanh A, B. Anh An thống kê số tiền thu được mỗi tháng trong vòng 60 ngày theo mỗi lĩnh vực có kết quả như sau:

So sánh giá trị trung bình và độ lệch chuẩn của số tiền thu được mỗi tháng khi đầu tư vào mỗi lĩnh vực A, B. Đầu tư vào lĩnh vực nào “rủi ro” hơn?
Giải:
Chọn giá trị đại diện cho các nhóm số liệu ta có:

Số tiền trung bình thu được khi đầu tư vào các lĩnh vực A, B tương ứng là:
\(\overline {{x_A}} = \frac{1}{{60}}(5.7,5 + ... + 5.27,5) = 17,5\) (triệu đồng)
\(\overline {{x_B}} = \frac{1}{{60}}(20.7,5 + ... + 20.27,5) = 17,5\) (triệu đồng)
Như vậy, về trung bình đầu tư vào các lĩnh vực A, B số tiền thu được hàng tháng như nhau
Độ lệch chuẩn của số tiền thu được hàng tháng khi đầu tư vào các lĩnh vực A, B tương ứng là:
\({s_A} = \sqrt {\frac{1}{{60}}(5.7,{5^2} + ... + 5.27,{5^2} - 17,{5^2}} = 5\)
\({s_B} = \sqrt {\frac{1}{{60}}(20.7,{5^2} + ... + 20.27,{5^2} - 17,{5^2}} \approx 8,42\)
Như vậy, độ lệch chuẩn của mẫu số liệu về số tiền thu được hàng tháng khi đầu tư vào lĩnh vực B cao hơn khi đầu tư vào lĩnh vực A. Người ta nói rằng, đầu tư vào lĩnh vực B là “rủi ro” hơn
Trong chương trình Toán 12 Kết nối tri thức, Phương sai và Độ lệch chuẩn là hai khái niệm thống kê quan trọng, dùng để đo lường mức độ phân tán của một tập dữ liệu so với giá trị trung bình. Hiểu rõ hai khái niệm này là nền tảng để phân tích và so sánh các tập dữ liệu khác nhau.
Phương sai (Variance), ký hiệu là σ2 (trong trường hợp tổng thể) hoặc s2 (trong trường hợp mẫu), là giá trị trung bình của bình phương độ lệch của mỗi giá trị trong tập dữ liệu so với giá trị trung bình của tập dữ liệu đó.
Công thức tính phương sai:
Độ lệch chuẩn (Standard Deviation), ký hiệu là σ (trong trường hợp tổng thể) hoặc s (trong trường hợp mẫu), là căn bậc hai của phương sai. Độ lệch chuẩn cho biết mức độ phân tán của dữ liệu xung quanh giá trị trung bình.
Công thức tính độ lệch chuẩn:
Phương sai và Độ lệch chuẩn có mối quan hệ mật thiết với nhau. Độ lệch chuẩn là căn bậc hai của phương sai. Do đó, nếu phương sai lớn, độ lệch chuẩn cũng lớn, và ngược lại. Độ lệch chuẩn thường được sử dụng phổ biến hơn vì nó có cùng đơn vị đo với dữ liệu gốc, giúp dễ dàng diễn giải.
Phương sai và Độ lệch chuẩn cung cấp thông tin quan trọng về sự biến thiên của dữ liệu:
Ví dụ 1: Cho một tập dữ liệu gồm các điểm thi Toán của 5 học sinh: 7, 8, 9, 6, 10. Tính phương sai và độ lệch chuẩn của tập dữ liệu này.
Ví dụ 2: So sánh hai tập dữ liệu:
| Tập dữ liệu | Giá trị trung bình | Phương sai | Độ lệch chuẩn |
|---|---|---|---|
| A: 1, 2, 3, 4, 5 | 3 | 2 | 1.41 |
| B: 1, 3, 5, 7, 9 | 5 | 8 | 2.83 |
Từ bảng trên, ta thấy tập dữ liệu B có phương sai và độ lệch chuẩn lớn hơn tập dữ liệu A, cho thấy dữ liệu B phân tán rộng hơn so với giá trị trung bình.
Phương sai và Độ lệch chuẩn được ứng dụng rộng rãi trong nhiều lĩnh vực:
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về Lý thuyết Phương sai và Độ lệch chuẩn Toán 12 Kết nối tri thức. Hãy luyện tập thêm các bài tập để nắm vững kiến thức này nhé!