Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 12, 13, 14 sách giáo khoa Toán 12 tập 2 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học.
Khái niệm tích phân
Trả lời câu hỏi Hoạt động 3 trang 14 SGK Toán 12 Kết nối tri thức
Giả sử f(x) là hàm số liên tục trên đoạn \(\left[ {a;b} \right]\), F(x) và G(x) là hai nguyên hàm tùy ý của f(x) trên đoạn \(\left[ {a;b} \right]\). Chứng minh rằng \(F\left( b \right) - F\left( a \right) = G\left( b \right) - G\left( a \right)\).
Phương pháp giải:
Sử dụng kiến thức về họ nguyên hàm của một hàm số để chứng minh: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.
Lời giải chi tiết:
Vì F(x) và G(x) là hai nguyên hàm tùy ý của f(x) trên đoạn \(\left[ {a;b} \right]\) nên tồn tại hằng số C sao cho \(F\left( x \right) = G\left( x \right) + C\).
Do đó, \(F\left( b \right) - F\left( a \right) = G\left( b \right) + C - G\left( a \right) - C = G\left( b \right) - G\left( a \right)\)
Trả lời câu hỏi Luyện tập 1 trang 15 SGK Toán 12 Kết nối tri thức
Tính:
a) \(\int\limits_0^1 {{e^x}dx} \);
b) \(\int\limits_1^e {\frac{1}{x}dx} \);
c) \(\int\limits_0^{\frac{\pi }{2}} {\sin xdx} \);
d) \(\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{3}} {\frac{{dx}}{{{{\sin }^2}x}}} \).
Phương pháp giải:
Sử dụng kiến thức về định nghĩa tích phân để tính: Cho f(x) là hàm số liên tục trên đoạn [a; b]. Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a; b] thì hiệu số \(F\left( b \right) - F\left( a \right)\) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu \(\int\limits_a^b {f\left( x \right)dx} \).
Lời giải chi tiết:
a) \(\int\limits_0^1 {{e^x}dx} = {e^x}\left| \begin{array}{l}1\\0\end{array} \right. = {e^1} - {e^0} = e - 1\);
b) \(\int\limits_1^e {\frac{1}{x}dx} = \ln \left| x \right|\left| \begin{array}{l}e\\1\end{array} \right. = \ln e - \ln 1 = 1\);
c) \(\int\limits_0^{\frac{\pi }{2}} {\sin xdx} = - \cos x\left| \begin{array}{l}\frac{\pi }{2}\\0\end{array} \right. = - \cos \frac{\pi }{2} + \cos 0 = 1\);
d) \(\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{3}} {\frac{{dx}}{{{{\sin }^2}x}}} = - \tan x\left| \begin{array}{l}\frac{\pi }{3}\\\frac{\pi }{6}\end{array} \right. = - \cot \frac{\pi }{3} + \cot \frac{\pi }{6} = - \frac{{\sqrt 3 }}{3} + \sqrt 3 = \frac{{2\sqrt 3 }}{3}\).
Trả lời câu hỏi Vận dụng 1 trang 16 SGK Toán 12 Kết nối tri thức
Giải quyết bài toán ở tình huống mở đầu.
Phương pháp giải:
Sử dụng kiến thức về định nghĩa tích phân để tính: Cho f(x) là hàm số liên tục trên đoạn [a; b]. Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a; b] thì hiệu số \(F\left( b \right) - F\left( a \right)\) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu \(\int\limits_a^b {f\left( x \right)dx} \)
Sử dụng kiến thức về quan hệ giữa hàm số vận tốc và hàm số quãng đường để tính: Hàm số quãng đường S(t) là một nguyên hàm của hàm số vận tốc v(t).
Lời giải chi tiết:
Lấy mốc thời gian là lúc ô tô bắt đầu được phanh. Gọi T là thời điểm ô tô dừng.
Xe dừng hẳn khi \(v\left( T \right) = 0.\) Do đó, \(0 = - 40T + 20\) nên \(T = \frac{1}{2}\). Như vậy, khoảng thời gian từ lúc đạp phanh đến khi dừng hẳn của ô tô là 0,5 giây.
Vì \(v\left( t \right) = S'\left( t \right)\) nên S(t) là một nguyên hàm của hàm vận tốc v(t).
Từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được số mét là:
Do đó, \(S\left( t \right) = \int\limits_0^{\frac{1}{2}} {v\left( t \right)dt} = \int\limits_0^{\frac{1}{2}} {\left( { - 40t + 20} \right)dt = \left( { - 20{t^2} + 20t} \right)\left| \begin{array}{l}\frac{1}{2}\\0\end{array} \right. = } - 20.{\left( {\frac{1}{2}} \right)^2} + 20.\frac{1}{2} = 5\left( m \right)\)
Vậy từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được 5m.
Trả lời câu hỏi Hoạt động 2 trang 13 SGK Toán 12 Kết nối tri thức
Xét hình thang cong giới hạn bởi đồ thị \(y = {x^2}\), trục hoành và hai đường thẳng \(x = 1,x = 2\). Ta muốn tính diện tích S của hình thang cong này.
a) Với mỗi \(x \in \left[ {1;2} \right]\), gọi S(x) là diện tích phần hình thang cong đã cho nằm giữa hai đường thẳng vuông góc với trục Ox tại điểm có hoành độ bằng 1 và x (H.4.5).
Cho \(h > 0\) sao cho \(x + h < 2\). So sánh hiệu \(S\left( {x + h} \right) - S\left( x \right)\) với diện tích hai hình chữ nhật MNPQ và MNEF (H.4.6). Từ đó suy ra: \(0 \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 2xh + {h^2}\).
b) Cho \(h < 0\) sao cho \(x + h > 1\). Tương tự phần a, đánh giá hiệu \(S\left( x \right) - S\left( {x + h} \right)\) và từ đó suy ra \(2xh + {h^2} \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 0\).
c) Từ kết quả phần a và phần b, suy ra với mọi \(h \ne 0\), ta có
\(\left| {\frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2}} \right| \le 2x\left| h \right| + {h^2}\).
Từ đó chứng minh \(S'\left( x \right) = {x^2},x \in \left( {1;2} \right)\). Người ta chứng minh được \(S'\left( 1 \right) = 1,S'\left( 2 \right) = 4\), tức là S(x) là một nguyên hàm của \({x^2}\) trên \(\left[ {1;2} \right]\).
d) Từ kết quả của phần c, ta có \(S\left( x \right) = \frac{{{x^3}}}{3} + C\). Sử dụng điều này với lưu ý \(S\left( 1 \right) = 0\) và diện tích cần tính \(S = S\left( 2 \right)\), hãy tính S.
Gọi F(x) là một nguyên hàm tùy ý của \(f\left( x \right) = {x^2}\) trên \(\left[ {1;2} \right]\). Hãy so sánh S và \(F\left( 2 \right) - F\left( 1 \right)\).
Phương pháp giải:
Sử dụng kiến thức về hình thang cong để tính: Hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\), trong đó f(x) là hàm liên tục không âm trên đoạn [a; b] gọi là một hình thang cong.
Lời giải chi tiết:
a) Với \(h > 0\) sao cho \(x + h < 2\), gọi \({S_{MNPQ}}\) và \({S_{MNEF}}\) lần lượt là diện tích các hình chữ nhật MNPQ và MNEF thì \({S_{MNPQ}} \le S\left( {x + h} \right) - S\left( x \right) \le {S_{MNEF}}\)
Diện tích hình chữ nhật MNPQ là: \({S_{MNPQ}} = MN.MQ = \left( {x + h - x} \right){x^2} = h{x^2}\)
Diện tích hình chữ nhật MNEF là: \({S_{MNEF}} = MN.NE = \left( {x + h - x} \right){\left( {x + h} \right)^2} = h{\left( {x + h} \right)^2}\)
Do đó, \(h{x^2} \le S\left( {x + h} \right) - S\left( x \right) \le h{\left( {x + h} \right)^2}\). Vậy \(0 \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 2xh + {h^2}\)
b)
Với \(h < 0\) sao cho \(x + h > 1\), gọi \({S_{MNPQ}}\) và \({S_{MNEF}}\) lần lượt là diện tích các hình chữ nhật MNPQ và MNEF thì \({S_{MNPQ}} \le S\left( x \right) - S\left( {x + h} \right) \le {S_{MNEF}}\)
Diện tích hình chữ nhật MNPQ là: \({S_{MNPQ}} = MN.MQ = - h{\left( {x + h} \right)^2} > 0\)
Diện tích hình chữ nhật MNEF là: \({S_{MNEF}} = MN.NE = - h{x^2}\)
Do đó, \( - h{\left( {x + h} \right)^2} \le S\left( {x + h} \right) - S\left( x \right) \le - h{x^2}\)
Vậy \(2xh + {h^2} \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 0\) (do \(h < 0\) nên \( - h > 0\))
c) Từ phần a và phần b, suy ra với mọi \(h \ne 0\), ta có: \(\left| {\frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2}} \right| \le 2x\left| h \right| + {h^2}\)
Do đó, \(S'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} = {x^2},x \in \left( {1;2} \right)\). Suy ra, \(S'\left( 1 \right) = 1,S'\left( 2 \right) = 4\).
Do đó, S(x) là một nguyên hàm của \({x^2}\) trên \(\left[ {1;2} \right]\).
d) Theo c ta có: \(S\left( x \right) = \frac{{{x^3}}}{3} + C\), \(S\left( 1 \right) = 0\) nên \(\frac{1}{3} + C = 0 \Leftrightarrow C = \frac{{ - 1}}{3}\).
Do đó, \(S\left( x \right) = \frac{{{x^3}}}{3} - \frac{1}{3}\)
Diện tích cần tính là: \(S = S\left( 2 \right) = \frac{{{2^3}}}{3} - \frac{1}{3} = \frac{7}{3}\)
Vì F(x) là một nguyên hàm tùy ý của \(f\left( x \right) = {x^2}\) trên \(\left[ {1;2} \right]\) nên \(F\left( x \right) = \frac{{{x^3}}}{3} + C,C \in \mathbb{R}\)
Ta có: \(F\left( 2 \right) - F\left( 1 \right) = \frac{7}{3} - 0 = \frac{7}{3} = S\). Do đó, \(S = F\left( 2 \right) - F\left( 1 \right)\)
Trả lời câu hỏi Hoạt động 1 trang 13 SGK Toán 12 Kết nối tri thức
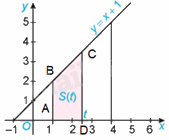
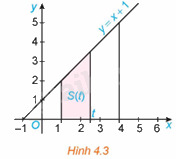
Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng \(y = x + 1\), trục hoành và hai đường thẳng \(x = 1,x = t\left( {1 \le t \le 4} \right)\) (H.4.3).
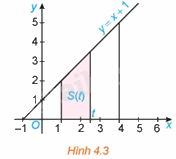
a) Tính diện tích S của T khi \(t = 4\).
b) Tính diện tích S(t) của T khi \(t \in \left[ {1;4} \right]\).
c) Chứng minh rằng S(t) là một nguyên hàm của hàm số \(f\left( t \right) = t + 1,t \in \left[ {1;4} \right]\) và diện tích \(S = S\left( 4 \right) - S\left( 1 \right)\).
Phương pháp giải:
Sử dụng kiến thức về diện tích hình thang để tính: Diện tích hình thang ABCD (AB//CD) là: \(S = \frac{{\left( {AB + CD} \right).h}}{2}\) với h là chiều cao của hình thang.
Lời giải chi tiết:
a) Gọi A, D lần lượt là giao điểm của các đường thẳng \(x = 1\), \(x = 4\) với trục hoành; B, C lần lượt là giao điểm của các đường thẳng \(x = 1\), \(x = 4\) với đường thẳng \(y = x + 1\).
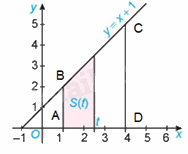
Khi đó, \(A\left( {1;0} \right),B\left( {1;2} \right),C\left( {4;5} \right),D\left( {4;0} \right)\). Do đó, \(AB = 2,CD = 5,AD = 3\)
Diện tích hình thang ABCD là: \(S = \frac{{\left( {AB + CD} \right).AD}}{2} = \frac{{\left( {2 + 5} \right).3}}{2} = \frac{{21}}{2}\)
b) Gọi A, D lần lượt là giao điểm của các đường thẳng \(x = 1\), \(x = t\) với trục hoành, B, C lần lượt là giao điểm của đường thẳng \(x = 1\), \(x = t\) với đường thẳng \(y = x + 1\).
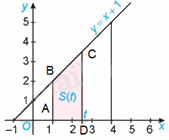
Khi đó, \(A\left( {1;0} \right),B\left( {1;2} \right),C\left( {t;t + 1} \right),D\left( {t;0} \right)\). Do đó, \(AB = 2,CD = t + 1,AD = t - 1\)
Diện tích hình thang ABCD là:
\(S\left( t \right) = \frac{{\left( {AB + CD} \right).AD}}{2} = \frac{{\left( {2 + t + 1} \right).\left( {t - 1} \right)}}{2} = \frac{{\left( {t + 3} \right)\left( {t - 1} \right)}}{2} = \frac{{{t^2} + 2t - 3}}{2}\)
c) Ta có: \(S'\left( t \right) = {\left( {\frac{{{t^2} + 2t - 3}}{2}} \right)'} = \frac{1}{2}\left( {2t + 2} \right) = t + 1 = f\left( t \right)\)
Do đó, S(t) là một nguyên hàm của hàm số \(f\left( t \right) = t + 1,t \in \left[ {1;4} \right]\).
Lại có: \(S\left( 4 \right) - S\left( 1 \right) = \frac{{{4^2} + 2.4 - 3}}{2} - \frac{{{1^2} + 2.1 - 3}}{2} = \frac{{21}}{2} - 0 = \frac{{21}}{2}\)
Suy ra: \(S = S\left( 4 \right) - S\left( 1 \right)\).
Trả lời câu hỏi Luyện tập 2 trang 16 SGK Toán 12 Kết nối tri thức
Sử dụng ý nghĩa hình học của tích phân, tính:
a) \(\int\limits_1^3 {\left( {2x + 1} \right)dx} \);
b) \(\int\limits_{ - 2}^2 {\sqrt {4 - {x^2}} dx} \).
Phương pháp giải:
Sử dụng kiến thức về ý nghĩa hình học của tích phân để tính: Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b], thì tích phân \(\int\limits_a^b {f\left( x \right)dx} \) là diện tích S của hình thang cong giới hạn bởi đồ thị \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\). Vậy \(S = \int\limits_a^b {f\left( x \right)dx} \).
Lời giải chi tiết:
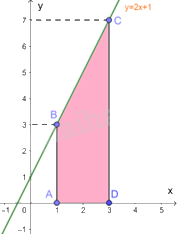
a) Tích phân cần tính là diện tích của hình thang vuông ABCD, có đáy nhỏ \(AB = 3,\) đáy lớn \(CD = 7\) và đường cao \(AD = 2\).
Do đó, \(\int\limits_1^3 {\left( {2x + 1} \right)dx} = {S_{ABCD}} = \frac{1}{2}\left( {AB + CD} \right)AD = \frac{1}{2}\left( {3 + 7} \right).2 = 10\)
b) Ta có \(y = \sqrt {4 - {x^2}} \) là phương trình nửa phía trên trục hoành của đường tròn tâm tại gốc tọa độ O và bán kính 2. Do đó, tích phân cần tính là diện tích nửa phía trên trục hoành của hình tròn tương ứng.
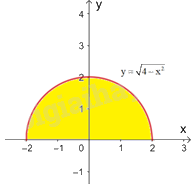
Vậy \(\int\limits_{ - 2}^2 {\sqrt {4 - {x^2}} dx} = 2\pi \)
Trả lời câu hỏi Hoạt động 1 trang 13 SGK Toán 12 Kết nối tri thức
Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng \(y = x + 1\), trục hoành và hai đường thẳng \(x = 1,x = t\left( {1 \le t \le 4} \right)\) (H.4.3).
a) Tính diện tích S của T khi \(t = 4\).
b) Tính diện tích S(t) của T khi \(t \in \left[ {1;4} \right]\).
c) Chứng minh rằng S(t) là một nguyên hàm của hàm số \(f\left( t \right) = t + 1,t \in \left[ {1;4} \right]\) và diện tích \(S = S\left( 4 \right) - S\left( 1 \right)\).
Phương pháp giải:
Sử dụng kiến thức về diện tích hình thang để tính: Diện tích hình thang ABCD (AB//CD) là: \(S = \frac{{\left( {AB + CD} \right).h}}{2}\) với h là chiều cao của hình thang.
Lời giải chi tiết:
a) Gọi A, D lần lượt là giao điểm của các đường thẳng \(x = 1\), \(x = 4\) với trục hoành; B, C lần lượt là giao điểm của các đường thẳng \(x = 1\), \(x = 4\) với đường thẳng \(y = x + 1\).
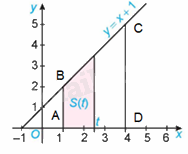
Khi đó, \(A\left( {1;0} \right),B\left( {1;2} \right),C\left( {4;5} \right),D\left( {4;0} \right)\). Do đó, \(AB = 2,CD = 5,AD = 3\)
Diện tích hình thang ABCD là: \(S = \frac{{\left( {AB + CD} \right).AD}}{2} = \frac{{\left( {2 + 5} \right).3}}{2} = \frac{{21}}{2}\)
b) Gọi A, D lần lượt là giao điểm của các đường thẳng \(x = 1\), \(x = t\) với trục hoành, B, C lần lượt là giao điểm của đường thẳng \(x = 1\), \(x = t\) với đường thẳng \(y = x + 1\).
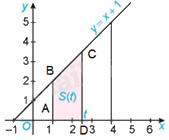
Khi đó, \(A\left( {1;0} \right),B\left( {1;2} \right),C\left( {t;t + 1} \right),D\left( {t;0} \right)\). Do đó, \(AB = 2,CD = t + 1,AD = t - 1\)
Diện tích hình thang ABCD là:
\(S\left( t \right) = \frac{{\left( {AB + CD} \right).AD}}{2} = \frac{{\left( {2 + t + 1} \right).\left( {t - 1} \right)}}{2} = \frac{{\left( {t + 3} \right)\left( {t - 1} \right)}}{2} = \frac{{{t^2} + 2t - 3}}{2}\)
c) Ta có: \(S'\left( t \right) = {\left( {\frac{{{t^2} + 2t - 3}}{2}} \right)'} = \frac{1}{2}\left( {2t + 2} \right) = t + 1 = f\left( t \right)\)
Do đó, S(t) là một nguyên hàm của hàm số \(f\left( t \right) = t + 1,t \in \left[ {1;4} \right]\).
Lại có: \(S\left( 4 \right) - S\left( 1 \right) = \frac{{{4^2} + 2.4 - 3}}{2} - \frac{{{1^2} + 2.1 - 3}}{2} = \frac{{21}}{2} - 0 = \frac{{21}}{2}\)
Suy ra: \(S = S\left( 4 \right) - S\left( 1 \right)\).
Trả lời câu hỏi Hoạt động 2 trang 13 SGK Toán 12 Kết nối tri thức
Xét hình thang cong giới hạn bởi đồ thị \(y = {x^2}\), trục hoành và hai đường thẳng \(x = 1,x = 2\). Ta muốn tính diện tích S của hình thang cong này.
a) Với mỗi \(x \in \left[ {1;2} \right]\), gọi S(x) là diện tích phần hình thang cong đã cho nằm giữa hai đường thẳng vuông góc với trục Ox tại điểm có hoành độ bằng 1 và x (H.4.5).
Cho \(h > 0\) sao cho \(x + h < 2\). So sánh hiệu \(S\left( {x + h} \right) - S\left( x \right)\) với diện tích hai hình chữ nhật MNPQ và MNEF (H.4.6). Từ đó suy ra: \(0 \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 2xh + {h^2}\).
b) Cho \(h < 0\) sao cho \(x + h > 1\). Tương tự phần a, đánh giá hiệu \(S\left( x \right) - S\left( {x + h} \right)\) và từ đó suy ra \(2xh + {h^2} \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 0\).
c) Từ kết quả phần a và phần b, suy ra với mọi \(h \ne 0\), ta có
\(\left| {\frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2}} \right| \le 2x\left| h \right| + {h^2}\).
Từ đó chứng minh \(S'\left( x \right) = {x^2},x \in \left( {1;2} \right)\). Người ta chứng minh được \(S'\left( 1 \right) = 1,S'\left( 2 \right) = 4\), tức là S(x) là một nguyên hàm của \({x^2}\) trên \(\left[ {1;2} \right]\).
d) Từ kết quả của phần c, ta có \(S\left( x \right) = \frac{{{x^3}}}{3} + C\). Sử dụng điều này với lưu ý \(S\left( 1 \right) = 0\) và diện tích cần tính \(S = S\left( 2 \right)\), hãy tính S.
Gọi F(x) là một nguyên hàm tùy ý của \(f\left( x \right) = {x^2}\) trên \(\left[ {1;2} \right]\). Hãy so sánh S và \(F\left( 2 \right) - F\left( 1 \right)\).
Phương pháp giải:
Sử dụng kiến thức về hình thang cong để tính: Hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\), trong đó f(x) là hàm liên tục không âm trên đoạn [a; b] gọi là một hình thang cong.
Lời giải chi tiết:
a) Với \(h > 0\) sao cho \(x + h < 2\), gọi \({S_{MNPQ}}\) và \({S_{MNEF}}\) lần lượt là diện tích các hình chữ nhật MNPQ và MNEF thì \({S_{MNPQ}} \le S\left( {x + h} \right) - S\left( x \right) \le {S_{MNEF}}\)
Diện tích hình chữ nhật MNPQ là: \({S_{MNPQ}} = MN.MQ = \left( {x + h - x} \right){x^2} = h{x^2}\)
Diện tích hình chữ nhật MNEF là: \({S_{MNEF}} = MN.NE = \left( {x + h - x} \right){\left( {x + h} \right)^2} = h{\left( {x + h} \right)^2}\)
Do đó, \(h{x^2} \le S\left( {x + h} \right) - S\left( x \right) \le h{\left( {x + h} \right)^2}\). Vậy \(0 \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 2xh + {h^2}\)
b)
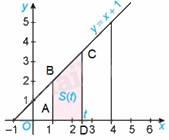
Với \(h < 0\) sao cho \(x + h > 1\), gọi \({S_{MNPQ}}\) và \({S_{MNEF}}\) lần lượt là diện tích các hình chữ nhật MNPQ và MNEF thì \({S_{MNPQ}} \le S\left( x \right) - S\left( {x + h} \right) \le {S_{MNEF}}\)
Diện tích hình chữ nhật MNPQ là: \({S_{MNPQ}} = MN.MQ = - h{\left( {x + h} \right)^2} > 0\)
Diện tích hình chữ nhật MNEF là: \({S_{MNEF}} = MN.NE = - h{x^2}\)
Do đó, \( - h{\left( {x + h} \right)^2} \le S\left( {x + h} \right) - S\left( x \right) \le - h{x^2}\)
Vậy \(2xh + {h^2} \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 0\) (do \(h < 0\) nên \( - h > 0\))
c) Từ phần a và phần b, suy ra với mọi \(h \ne 0\), ta có: \(\left| {\frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2}} \right| \le 2x\left| h \right| + {h^2}\)
Do đó, \(S'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} = {x^2},x \in \left( {1;2} \right)\). Suy ra, \(S'\left( 1 \right) = 1,S'\left( 2 \right) = 4\).
Do đó, S(x) là một nguyên hàm của \({x^2}\) trên \(\left[ {1;2} \right]\).
d) Theo c ta có: \(S\left( x \right) = \frac{{{x^3}}}{3} + C\), \(S\left( 1 \right) = 0\) nên \(\frac{1}{3} + C = 0 \Leftrightarrow C = \frac{{ - 1}}{3}\).
Do đó, \(S\left( x \right) = \frac{{{x^3}}}{3} - \frac{1}{3}\)
Diện tích cần tính là: \(S = S\left( 2 \right) = \frac{{{2^3}}}{3} - \frac{1}{3} = \frac{7}{3}\)
Vì F(x) là một nguyên hàm tùy ý của \(f\left( x \right) = {x^2}\) trên \(\left[ {1;2} \right]\) nên \(F\left( x \right) = \frac{{{x^3}}}{3} + C,C \in \mathbb{R}\)
Ta có: \(F\left( 2 \right) - F\left( 1 \right) = \frac{7}{3} - 0 = \frac{7}{3} = S\). Do đó, \(S = F\left( 2 \right) - F\left( 1 \right)\)
Trả lời câu hỏi Hoạt động 3 trang 14 SGK Toán 12 Kết nối tri thức
Giả sử f(x) là hàm số liên tục trên đoạn \(\left[ {a;b} \right]\), F(x) và G(x) là hai nguyên hàm tùy ý của f(x) trên đoạn \(\left[ {a;b} \right]\). Chứng minh rằng \(F\left( b \right) - F\left( a \right) = G\left( b \right) - G\left( a \right)\).
Phương pháp giải:
Sử dụng kiến thức về họ nguyên hàm của một hàm số để chứng minh: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.
Lời giải chi tiết:
Vì F(x) và G(x) là hai nguyên hàm tùy ý của f(x) trên đoạn \(\left[ {a;b} \right]\) nên tồn tại hằng số C sao cho \(F\left( x \right) = G\left( x \right) + C\).
Do đó, \(F\left( b \right) - F\left( a \right) = G\left( b \right) + C - G\left( a \right) - C = G\left( b \right) - G\left( a \right)\)
Trả lời câu hỏi Luyện tập 1 trang 15 SGK Toán 12 Kết nối tri thức
Tính:
a) \(\int\limits_0^1 {{e^x}dx} \);
b) \(\int\limits_1^e {\frac{1}{x}dx} \);
c) \(\int\limits_0^{\frac{\pi }{2}} {\sin xdx} \);
d) \(\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{3}} {\frac{{dx}}{{{{\sin }^2}x}}} \).
Phương pháp giải:
Sử dụng kiến thức về định nghĩa tích phân để tính: Cho f(x) là hàm số liên tục trên đoạn [a; b]. Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a; b] thì hiệu số \(F\left( b \right) - F\left( a \right)\) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu \(\int\limits_a^b {f\left( x \right)dx} \).
Lời giải chi tiết:
a) \(\int\limits_0^1 {{e^x}dx} = {e^x}\left| \begin{array}{l}1\\0\end{array} \right. = {e^1} - {e^0} = e - 1\);
b) \(\int\limits_1^e {\frac{1}{x}dx} = \ln \left| x \right|\left| \begin{array}{l}e\\1\end{array} \right. = \ln e - \ln 1 = 1\);
c) \(\int\limits_0^{\frac{\pi }{2}} {\sin xdx} = - \cos x\left| \begin{array}{l}\frac{\pi }{2}\\0\end{array} \right. = - \cos \frac{\pi }{2} + \cos 0 = 1\);
d) \(\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{3}} {\frac{{dx}}{{{{\sin }^2}x}}} = - \tan x\left| \begin{array}{l}\frac{\pi }{3}\\\frac{\pi }{6}\end{array} \right. = - \cot \frac{\pi }{3} + \cot \frac{\pi }{6} = - \frac{{\sqrt 3 }}{3} + \sqrt 3 = \frac{{2\sqrt 3 }}{3}\).
Trả lời câu hỏi Luyện tập 2 trang 16 SGK Toán 12 Kết nối tri thức
Sử dụng ý nghĩa hình học của tích phân, tính:
a) \(\int\limits_1^3 {\left( {2x + 1} \right)dx} \);
b) \(\int\limits_{ - 2}^2 {\sqrt {4 - {x^2}} dx} \).
Phương pháp giải:
Sử dụng kiến thức về ý nghĩa hình học của tích phân để tính: Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b], thì tích phân \(\int\limits_a^b {f\left( x \right)dx} \) là diện tích S của hình thang cong giới hạn bởi đồ thị \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\). Vậy \(S = \int\limits_a^b {f\left( x \right)dx} \).
Lời giải chi tiết:
a) Tích phân cần tính là diện tích của hình thang vuông ABCD, có đáy nhỏ \(AB = 3,\) đáy lớn \(CD = 7\) và đường cao \(AD = 2\).
Do đó, \(\int\limits_1^3 {\left( {2x + 1} \right)dx} = {S_{ABCD}} = \frac{1}{2}\left( {AB + CD} \right)AD = \frac{1}{2}\left( {3 + 7} \right).2 = 10\)
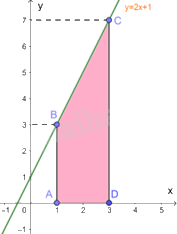
b) Ta có \(y = \sqrt {4 - {x^2}} \) là phương trình nửa phía trên trục hoành của đường tròn tâm tại gốc tọa độ O và bán kính 2. Do đó, tích phân cần tính là diện tích nửa phía trên trục hoành của hình tròn tương ứng.
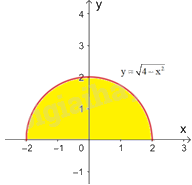
Vậy \(\int\limits_{ - 2}^2 {\sqrt {4 - {x^2}} dx} = 2\pi \)
Trả lời câu hỏi Vận dụng 1 trang 16 SGK Toán 12 Kết nối tri thức
Giải quyết bài toán ở tình huống mở đầu.
Phương pháp giải:
Sử dụng kiến thức về định nghĩa tích phân để tính: Cho f(x) là hàm số liên tục trên đoạn [a; b]. Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a; b] thì hiệu số \(F\left( b \right) - F\left( a \right)\) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu \(\int\limits_a^b {f\left( x \right)dx} \)
Sử dụng kiến thức về quan hệ giữa hàm số vận tốc và hàm số quãng đường để tính: Hàm số quãng đường S(t) là một nguyên hàm của hàm số vận tốc v(t).
Lời giải chi tiết:
Lấy mốc thời gian là lúc ô tô bắt đầu được phanh. Gọi T là thời điểm ô tô dừng.
Xe dừng hẳn khi \(v\left( T \right) = 0.\) Do đó, \(0 = - 40T + 20\) nên \(T = \frac{1}{2}\). Như vậy, khoảng thời gian từ lúc đạp phanh đến khi dừng hẳn của ô tô là 0,5 giây.
Vì \(v\left( t \right) = S'\left( t \right)\) nên S(t) là một nguyên hàm của hàm vận tốc v(t).
Từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được số mét là:
Do đó, \(S\left( t \right) = \int\limits_0^{\frac{1}{2}} {v\left( t \right)dt} = \int\limits_0^{\frac{1}{2}} {\left( { - 40t + 20} \right)dt = \left( { - 20{t^2} + 20t} \right)\left| \begin{array}{l}\frac{1}{2}\\0\end{array} \right. = } - 20.{\left( {\frac{1}{2}} \right)^2} + 20.\frac{1}{2} = 5\left( m \right)\)
Vậy từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được 5m.
Mục 1 của chương trình Toán 12 tập 2 - Kết nối tri thức thường tập trung vào một chủ đề quan trọng, đặt nền móng cho các kiến thức tiếp theo. Việc nắm vững nội dung và phương pháp giải các bài tập trong mục này là vô cùng cần thiết. Bài viết này sẽ đi sâu vào từng bài tập trang 12, 13, 14, cung cấp lời giải chi tiết, phân tích các bước thực hiện và giải thích các khái niệm liên quan.
Chúng ta sẽ bắt đầu với việc giải chi tiết các bài tập từ 1 đến hết trang 12. Đối với mỗi bài tập, chúng tôi sẽ:
Tiếp theo, chúng ta sẽ chuyển sang giải các bài tập trên trang 13. Các bài tập này có thể có độ khó cao hơn, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học. Chúng tôi sẽ cung cấp các lời giải chi tiết, kèm theo các lưu ý quan trọng để giúp các em hiểu rõ hơn về cách giải.
Cuối cùng, chúng ta sẽ giải các bài tập còn lại trên trang 14. Đây thường là các bài tập tổng hợp, yêu cầu học sinh phải kết hợp nhiều kiến thức khác nhau. Chúng tôi sẽ hướng dẫn các em cách tiếp cận và giải quyết các bài tập này một cách hiệu quả.
Trong quá trình giải các bài tập, chúng ta sẽ gặp một số kiến thức quan trọng sau:
Các kiến thức này không chỉ quan trọng trong chương trình Toán 12 mà còn là nền tảng cho các môn học khác và ứng dụng trong thực tế.
Để học tập và ôn thi môn Toán 12 hiệu quả, các em nên:
Hy vọng rằng bài viết này đã cung cấp cho các em những lời giải chi tiết và hữu ích cho các bài tập trong mục 1 trang 12, 13, 14 SGK Toán 12 tập 2 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Bài tập | Lời giải |
|---|---|
| Bài tập 1 (Trang 12) | [Link đến lời giải chi tiết] |
| Bài tập 2 (Trang 12) | [Link đến lời giải chi tiết] |
| ... | ... |