Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 1.25 trang 32 SGK Toán 12 tập 1 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
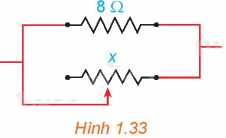
Trong Vật lí, ta biết rằng khi mắc song song hai điện trở \({R_1}\) và \({R_2}\) thì điện trở tương đương R của mạch điện được tính theo công thức \(R = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\) (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016). Giả sử một điện trở \(8\Omega \) được mắc song song với một biến trở như Hình 1.33. Nếu điện trở đó được kí hiệu là \(x\left( \Omega \right)\) thì điện trở tương đương R là hàm số của x. Vẽ đồ thị của hàm số \(y = R\left( x \right),x > 0\) và dựa vào đ
Đề bài
Trong Vật lí, ta biết rằng khi mắc song song hai điện trở \({R_1}\) và \({R_2}\) thì điện trở tương đương R của mạch điện được tính theo công thức \(R = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\) (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016).
Giả sử một điện trở \(8\Omega \) được mắc song song với một biến trở như Hình 1.33. Nếu điện trở đó được kí hiệu là \(x\left( \Omega \right)\) thì điện trở tương đương R là hàm số của x. Vẽ đồ thị của hàm số \(y = R\left( x \right),x > 0\) và dựa vào đồ thị đã vẽ, hãy cho biết:
a) Điện trở tương đương của mạch thay đổi thế nào khi x tăng.
b) Tại sao điện trở tương đương của mạch không bao giờ vượt quá \(8\Omega \).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về sơ đồ khảo sát hàm số phân thức để khảo sát và vẽ đồ thị hàm số:
Sơ đồ khảo sát hàm số phân thức
1. Tìm tập xác định của hàm số.
2. Khảo sát sự biến thiên của hàm số:
+ Tính đạo hàm y’. Tìm các điểm tại đó y’ bằng 0 hoặc đạo hàm không tồn tại.
+ Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số.
+ Tìm cực trị của hàm số.
+ Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số.
+ Lập bảng biến thiên của hàm số.
3. Vẽ đồ thị của hàm số dựa vào bảng biến thiên.
Lời giải chi tiết
Khi một điện trở \(8\Omega \) được mắc song song với một biến trở \(x\left( \Omega \right)\) thì điện trở tương đương của mạch là: \(R\left( x \right) = \frac{{8x}}{{x + 8}}\left( \Omega \right)\)
Vẽ đồ thị hàm số \(y = R\left( x \right) = \frac{{8x}}{{x + 8}}\) với \(x > 0\).
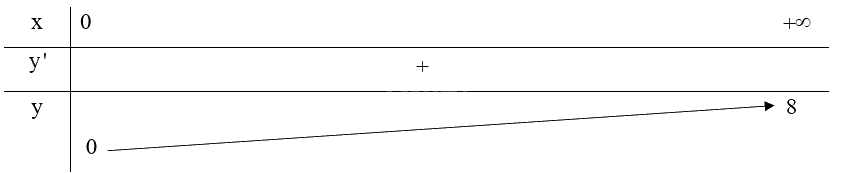
1. Tập xác định của hàm số: \(\left( {0; + \infty } \right)\)
2. Sự biến thiên:
\(R'\left( x \right) = \frac{{64}}{{{{\left( {x + 8} \right)}^2}}} > 0\forall x > 0\)
Hàm số đồng trên \(\left( {0; + \infty } \right)\).
Hàm số không có cực trị.
\(\mathop {\lim }\limits_{x \to + \infty } R\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{8x}}{{x + 8}} = 8\).
Do đó, đồ thị hàm số \(y = R\left( x \right) = \frac{{8x}}{{x + 8}}\) với \(x > 0\) nhận đường thẳng \(y = 8\) làm tiệm cận ngang (phần bên phải trục Oy).
Bảng biến thiên:
3. Đồ thị:
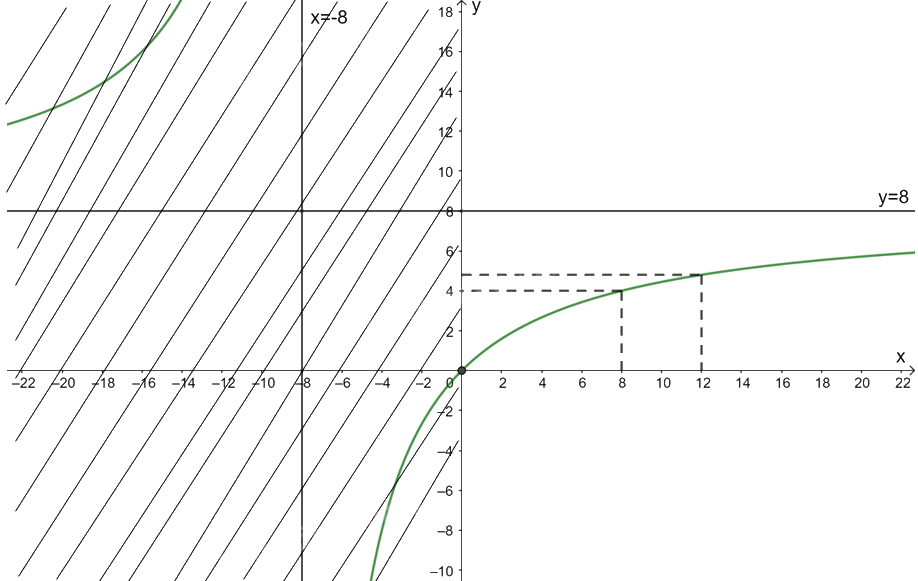
Giao điểm của đồ thị hàm số với trục tung là (0; 0).
Đồ thị hàm số \(y = R\left( x \right) = \frac{{8x}}{{x + 8}}\) đi qua các điểm (8; 4); \(\left( {12;\frac{{24}}{5}} \right)\).
a) Vì \(R'\left( x \right) = \frac{{64}}{{{{\left( {x + 8} \right)}^2}}} > 0\forall x > 0\) nên khi x tăng thì điện trở tương đương của mạch tăng.
b) Vì \(R'\left( x \right) = \frac{{64}}{{{{\left( {x + 8} \right)}^2}}} > 0\forall x > 0\) và \(\mathop {\lim }\limits_{x \to + \infty } R\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{8x}}{{x + 8}} = 8\) nên điện trở tương đương của mạch không bao giờ vượt quá \(8\Omega \).
Bài tập 1.25 trang 32 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương 1: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai, điều kiện xác định của hàm số và các phép biến đổi hàm số để giải quyết.
Bài tập 1.25 thường có dạng xác định tập xác định của hàm số, tìm tập giá trị của hàm số, hoặc xét tính đơn điệu của hàm số. Để giải quyết bài tập này, học sinh cần nắm vững các khái niệm cơ bản về hàm số bậc hai, bao gồm:
Để giải bài tập 1.25 trang 32 SGK Toán 12 tập 1 - Kết nối tri thức, bạn có thể áp dụng các phương pháp sau:
Bài tập: Tìm tập xác định của hàm số y = √(x2 - 4x + 3)
Lời giải:
Để hàm số y = √(x2 - 4x + 3) có nghĩa, điều kiện là x2 - 4x + 3 ≥ 0.
Ta phân tích đa thức x2 - 4x + 3 = (x - 1)(x - 3).
Để (x - 1)(x - 3) ≥ 0, ta xét các trường hợp:
Vậy tập xác định của hàm số là D = (-∞; 1] ∪ [3; +∞).
Khi giải bài tập 1.25, bạn cần chú ý các điểm sau:
Để củng cố kiến thức và kỹ năng giải bài tập 1.25, bạn có thể làm thêm các bài tập tương tự trong SGK Toán 12 tập 1 - Kết nối tri thức và các tài liệu tham khảo khác. Ngoài ra, bạn có thể tìm kiếm các bài giảng online hoặc tham gia các khóa học luyện thi Toán 12 để được hướng dẫn chi tiết hơn.
Bài tập 1.25 trang 32 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải quyết các bài toán liên quan đến hàm số. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn khi giải bài tập và đạt kết quả tốt trong môn Toán.