Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 2 trang 27 và 28 sách giáo khoa Toán 12 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là cung cấp cho các em những lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Khảo sát và vẽ đồ thị hàm số đa thức bậc 3
Đề bài
Trả lời câu hỏi Luyện tập 1 trang 28 SGK Toán 12 Kết nối tri thức
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = - 2{x^3} + 3{x^2} - 5x\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về sơ đồ khảo sát hàm số bậc ba để khảo sát và vẽ đồ thị hàm số:
Sơ đồ khảo sát hàm số bậc ba
1. Tìm tập xác định của hàm số.
2. Khảo sát sự biến thiên của hàm số:
+ Tính đạo hàm y’. Tìm các điểm tại đó y’ bằng 0 hoặc đạo hàm không tồn tại.
+ Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số.
+ Tìm cực trị của hàm số.
+ Tìm các giới hạn tại vô cực, giới hạn vô cực.
+ Lập bảng biến thiên của hàm số.
3. Vẽ đồ thị của hàm số dựa vào bảng biến thiên.
Lời giải chi tiết
1. Tập xác định: \(D = \mathbb{R}\)
2. Sự biến thiên:
Ta có: \(y' = - 6{x^2} + 6x - 5 = - 6{\left( {x - \frac{1}{2}} \right)^2} - \frac{7}{2} \le - \frac{7}{2}\) với mọi \(x \in \mathbb{R}\)
Hàm số nghịch biến trên \(\left( { - \infty ; + \infty } \right)\).
Hàm số không có cực trị.
Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( { - 2{x^3} + 3{x^2} - 5x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {{x^3}\left( { - 2 + \frac{3}{x} - \frac{3}{{{x^2}}}} \right)} \right] = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( { - 2{x^3} + 3{x^2} - 5x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {{x^3}\left( { - 2 + \frac{3}{x} - \frac{3}{{{x^2}}}} \right)} \right] = - \infty \)
Bảng biến thiên:
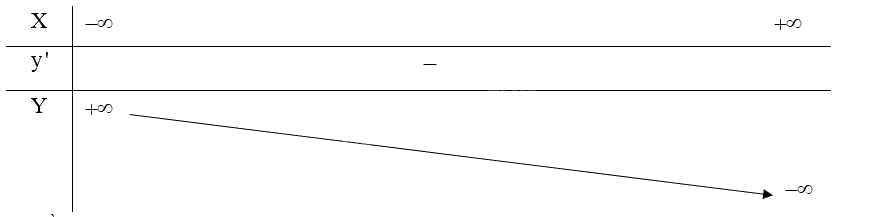
3. Đồ thị:
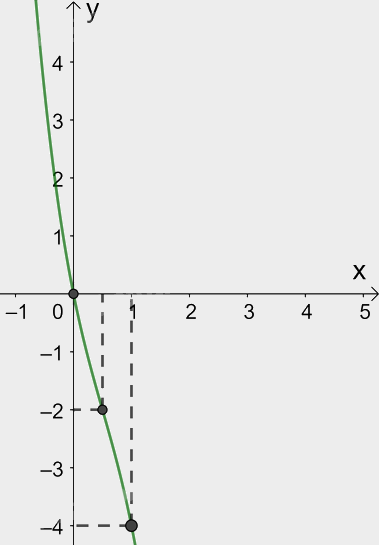
Giao điểm của đồ thị hàm số \(y = - 2{x^3} + 3{x^2} - 5x\) với trục tung là \(\left( {0;0} \right)\).
Ta có: \( - 2{x^3} + 3{x^2} - 5x = 0 \Leftrightarrow - x\left( {2{x^2} - 3x + 5} \right) = 0 \Leftrightarrow x = 0\). Do đó, giao điểm của đồ thị hàm số với trục hoành là điểm (0; 0).
Điểm \(\left( {1; - 4} \right)\) thuộc đồ thị hàm số \(y = - 2{x^3} + 3{x^2} - 5x\).
Đồ thị hàm số có tâm đối xứng là điểm \(\left( {\frac{1}{2}; - 2} \right)\).
Mục 2 của chương trình Toán 12 tập 1 Kết nối tri thức tập trung vào việc nghiên cứu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng, đóng vai trò then chốt trong việc hiểu và giải quyết các bài toán về đạo hàm, tích phân và các ứng dụng của chúng trong các lĩnh vực khác.
Mục 2 bao gồm các nội dung chính sau:
Dưới đây là lời giải chi tiết cho các bài tập trang 27 SGK Toán 12 tập 1 Kết nối tri thức:
Tiếp theo, chúng ta sẽ cùng giải chi tiết các bài tập trang 28 SGK Toán 12 tập 1 Kết nối tri thức:
Để giải tốt các bài tập về giới hạn, các em cần lưu ý những điều sau:
Ví dụ: Tìm tiệm cận đứng của hàm số y = (x+1)/(x-2). Giải: Giới hạn của hàm số khi x tiến tới 2 là vô cùng, do đó đường thẳng x = 2 là tiệm cận đứng của hàm số.
Để hiểu sâu hơn về giới hạn, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với những lời giải chi tiết và những lưu ý trên, các em sẽ tự tin hơn trong việc giải các bài tập về giới hạn của hàm số. Chúc các em học tập tốt!