Bài tập 2.23 trang 72 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 2.23, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
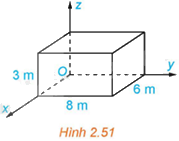
Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 8m, chiều rộng là 6m và chiều cao là 3m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục tọa độ Oxyz có gốc O trùng với một góc phòng và mặt phẳng (Oxy) trùng với mặt sàn, đơn vị đo được lấy theo mét (H.2.51). Hãy tìm tọa độ của điểm treo đèn.
Đề bài
Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 8m, chiều rộng là 6m và chiều cao là 3m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục tọa độ Oxyz có gốc O trùng với một góc phòng và mặt phẳng (Oxy) trùng với mặt sàn, đơn vị đo được lấy theo mét (H.2.51). Hãy tìm tọa độ của điểm treo đèn.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tọa độ trung điểm của đoạn thẳng để tính: Trong không gian Oxyz, cho hai điểm \(A\left( {{x_A};{y_A};{z_A}} \right)\) và \(B\left( {{x_B};{y_B};{z_B}} \right)\). Khi đó, tọa độ trung điểm của đoạn thẳng AB là: \(\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2}} \right)\).
Lời giải chi tiết
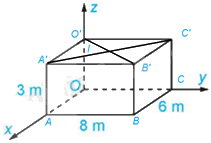
Đặt tên các điểm như hình vẽ.
Khi đó, \(O'\left( {0;0;3} \right),B'\left( {6;8;3} \right)\).
Vì phòng học thiết kế dạng hình hộp chữ nhật nên hình O’C’B’A’ là hình chữ nhật. Gọi là giao điểm của hai đường chéo O’B’ và A’C’ nên I là trung điểm của O’B’.
Vì đèn được treo tại chính giữa trần nhà của phòng học nên đèn trùng với I.
Do đó: \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_{O'}} + {x_{B'}}}}{2} = 3\\{y_I} = \frac{{{y_{O'}} + {y_{B'}}}}{2} = 4\\{z_I} = \frac{{{z_{O'}} + {z_{B'}}}}{2} = 3\end{array} \right.\). Suy ra, I(3; 4; 3). Vậy tọa độ của điểm treo đèn là (3; 4; 3).
Bài tập 2.23 trang 72 SGK Toán 12 tập 1 - Kết nối tri thức là một bài toán quan trọng trong chương trình học về đạo hàm. Bài toán này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
Bài tập 2.23 thường có dạng như sau: Cho hàm số f(x). Tìm đạo hàm f'(x) và sử dụng đạo hàm để giải quyết một bài toán cụ thể, ví dụ như tìm cực trị của hàm số, xét tính đơn điệu của hàm số, hoặc giải phương trình, bất phương trình.
Để giải bài tập 2.23 một cách hiệu quả, học sinh cần thực hiện các bước sau:
Ví dụ: Cho hàm số f(x) = x3 - 3x2 + 2. Tìm cực trị của hàm số.
Giải:
Khi giải bài tập về đạo hàm, học sinh cần lưu ý một số điểm sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Để học tốt về đạo hàm, học sinh có thể tham khảo các tài liệu sau:
Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải bài tập 2.23 trang 72 SGK Toán 12 tập 1 - Kết nối tri thức và các bài tập tương tự.