Bài tập 1.7 trang 14 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Kết nối tri thức, tập trung vào việc rèn luyện kỹ năng về giới hạn của hàm số. Bài tập này thường yêu cầu học sinh vận dụng các định nghĩa và tính chất của giới hạn để tính toán và chứng minh.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 1.7 trang 14 SGK Toán 12 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tìm cực trị của các hàm số sau: a) (y = 2{x^3} - 9{x^2} + 12x - 5);(y = {x^4} - 4{x^2} + 2) b) ; c) (y = frac{{{x^2} - 2x + 3}}{{x - 1}}); d) (y = sqrt {4x - 2{x^2}} ).
Đề bài
Tìm cực trị của các hàm số sau:a) \(y = 2{x^3} - 9{x^2} + 12x - 5\);b) \(y = {x^4} - 4{x^2} + 2\);c) \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\);d) \(y = \sqrt {4x - 2{x^2}} \).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về cách tìm cực trị của hàm số để tìm cực trị của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Lời giải chi tiết
a) Tập xác định: \(D = \mathbb{R}\).
\(y' = 6{x^2} - 18x + 12\), \(y' = 0 \Leftrightarrow 6{x^2} - 18x + 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\)
Bảng biến thiên:
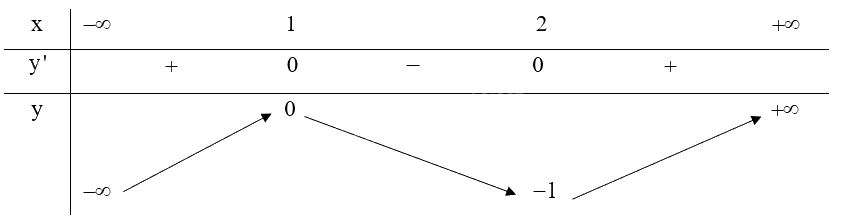
Từ bảng biến thiên ta có:
Hàm số \(y = 2{x^3} - 9{x^2} + 12x - 5\) có điểm cực đại là \(\left( {1;0} \right)\).
Hàm số \(y = 2{x^3} - 9{x^2} + 12x - 5\) có điểm cực tiểu là \(\left( {2; - 1} \right)\).
b) Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \(y' = 4{x^3} - 8x,y' = 0 \Leftrightarrow 4{x^3} - 8x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 2 \end{array} \right.\)
Bảng biến thiên:
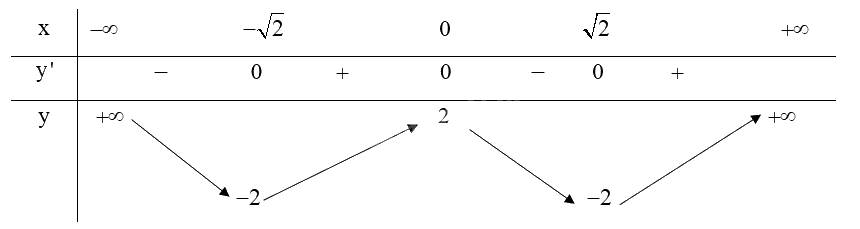
Từ bảng biến thiên ta có:
Hàm số \(y = {x^4} - 4{x^2} + 2\) đạt cực đại tại \(x = 0\) và \({y_{CĐ}} = 2\).
Hàm số \(y = {x^4} - 4{x^2} + 2\) đạt cực tiểu tại \(x = \pm \sqrt 2 \) và \({y_{CT}} = - 2\).
c) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).
Ta có: \(y' = \frac{{\left( {2x - 2} \right)\left( {x - 1} \right) - \left( {{x^2} - 2x + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}} = \frac{{{x^2} - 2x - 1}}{{{{\left( {x - 1} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 - \sqrt 2 \\x = 1 + \sqrt 2 \end{array} \right.\) (thỏa mãn)
Lập bảng biến thiên của hàm số:
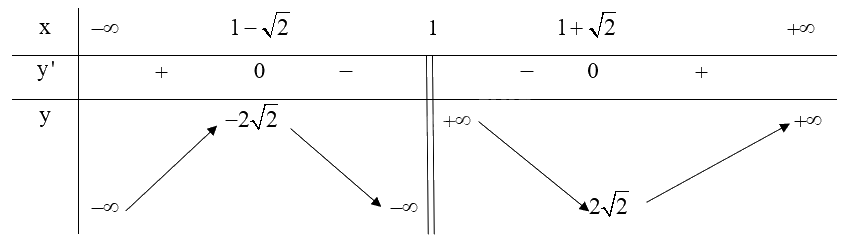
Từ bảng biến thiên ta có:
Hàm số \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\) đạt cực đại tại \(x = 1 - \sqrt 2 \) và \({y_{CĐ}} = -2\sqrt 2 \).
Hàm số \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\) đạt cực tiểu tại \(x = 1 + \sqrt 2 \) và \({y_{CT}} = 2\sqrt 2 \).
d) \(y = \sqrt {4x - 2{x^2}} \)
Tập xác định: \(D = \left[ {0;2} \right]\).
Ta có: \(y' = \frac{{\left( {4x - 2{x^2}} \right)'}}{{2\sqrt {4x - 2{x^2}} }} = \frac{2({ - x + 1})}{{\sqrt {4x - 2{x^2}} }},y' = 0 \Leftrightarrow x = 1\left( {tm} \right)\)
Ta có bảng biến thiên của hàm số:
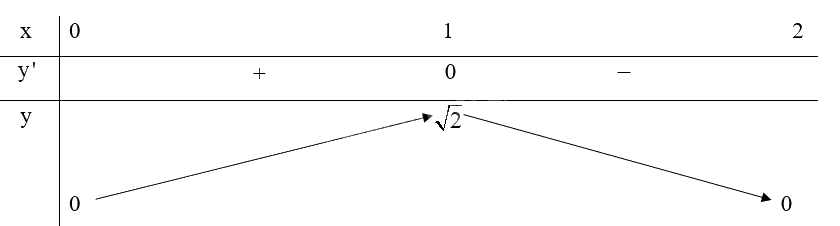
Do đó, hàm số đạt cực đại tại \(x = 1\), \({y_{CĐ}} = \sqrt 2 \), hàm số không có cực tiểu.
Bài tập 1.7 SGK Toán 12 tập 1 Kết nối tri thức yêu cầu tính các giới hạn sau:
Ta có thể phân tích tử thức:
x^2 - 3x + 2 = (x - 1)(x - 2)
Do đó:
lim (x→2) (x^2 - 3x + 2) / (x - 2) = lim (x→2) (x - 1)(x - 2) / (x - 2) = lim (x→2) (x - 1) = 2 - 1 = 1
Ta có thể phân tích tử thức:
x^3 + 1 = (x + 1)(x^2 - x + 1)
Do đó:
lim (x→-1) (x^3 + 1) / (x + 1) = lim (x→-1) (x + 1)(x^2 - x + 1) / (x + 1) = lim (x→-1) (x^2 - x + 1) = (-1)^2 - (-1) + 1 = 1 + 1 + 1 = 3
Để tính giới hạn này, ta sử dụng phương pháp nhân liên hợp:
lim (x→0) (√(x+1) - 1) / x = lim (x→0) [(√(x+1) - 1)(√(x+1) + 1)] / [x(√(x+1) + 1)]
= lim (x→0) (x + 1 - 1) / [x(√(x+1) + 1)] = lim (x→0) x / [x(√(x+1) + 1)] = lim (x→0) 1 / (√(x+1) + 1)
= 1 / (√(0+1) + 1) = 1 / (1 + 1) = 1/2
Vậy, kết quả của các giới hạn là:
Để hiểu rõ hơn về giới hạn hàm số, các em có thể tham khảo thêm các kiến thức sau:
Các em có thể tự luyện tập thêm các bài tập tương tự để củng cố kiến thức:
Khi tính giới hạn, cần chú ý đến các dạng vô định và sử dụng các phương pháp phù hợp để khử dạng vô định. Việc nắm vững các định nghĩa và tính chất của giới hạn là rất quan trọng để giải quyết các bài tập một cách chính xác và hiệu quả.