Bài tập 3.14 trang 86 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Kết nối tri thức, là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng và kiến thức đã học. Bài tập này thường liên quan đến các khái niệm về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 3.14 trang 86 SGK Toán 12 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Để đánh giá chất lượng một loại pin điện thoại mới, người ta ghi lại thời gian nghe nhạc liên tục của điện thoại được sạc đầy pin cho đến khi hết pin cho kết quả như sau: Tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
Đề bài
Để đánh giá chất lượng một loại pin điện thoại mới, người ta ghi lại thời gian nghe nhạc liên tục của điện thoại được sạc đầy pin cho đến khi hết pin cho kết quả như sau:
Tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về khoảng biến thiên của mẫu số liệu ghép nhóm để tính:
Cho mẫu số liệu ghép nhóm:
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: \(R = {a_{k + 1}} - {a_1}\).
+Sử dụng kiến thức về tính chất về nhóm chứa tứ phân vị của mẫu số liệu để tính: Ta có thể xác định nhóm chứa tứ phân vị thứ r nhờ tính chất: có khoảng \(\left( {\frac{{r.n}}{4}} \right)\) giá trị nhỏ hơn tứ phân vị này.
+ Sử dụng kiến thức về khoảng tứ phân vị của mẫu số liệu ghép nhóm để tính: Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu là \({\Delta _Q}\), là hiệu số giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).
+ Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm, kí hiệu là \({s^2}\), là một số được tính theo công thức sau: \({s^2} = \frac{1}{n}\left( {{m_1}x_1^2 + ... + {m_k}x_k^2} \right) - {\left( {\overline x } \right)^2}\), trong đó \(n = {m_1} + ... + {m_k}\) với \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm.
+ Sử dụng kiến thức độ lệch chuẩn của mẫu số liệu ghép nhóm để tính: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \).
Lời giải chi tiết
Khoảng biến thiên: \(R = 7,5 - 5 = 2,5\)
Cỡ mẫu: \(n = 2 + 8 + 15 + 10 + 5 = 40\)
Tứ phân vị thứ nhất của mẫu số liệu là: \(\frac{{{x_{10}} + {x_{11}}}}{2}\), vì \({x_{10}} \in \left[ {5,5;6} \right),{x_{11}} \in \left[ {6;6,5} \right)\) nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 6\).
Tứ phân vị thứ ba của mẫu số liệu là: \(\frac{{{x_{30}} + {x_{31}}}}{2}\) thuộc nhóm \(\left[ {6,5;7} \right)\) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 6,5 + \frac{{\frac{{3.40}}{4} - \left( {2 + 8 + 15} \right)}}{{10}}.0,5 = 6,75\).
Khoảng biến thiên: \({\Delta _Q} = {Q_3} - {Q_1} = 6,75 - 6 = 0,75\)
Chọn giá trị đại diện cho các nhóm số liệu, ta có: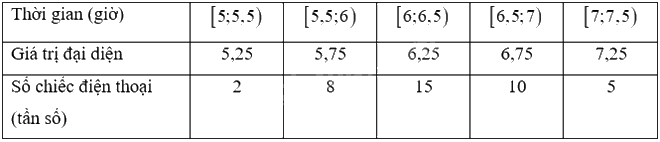
Thời gian trung bình nghe nhạc liên tục của điện thoại là: \(\overline x = \frac{1}{{40}}\left( {5,25.2 + 5,75.8 + 6,25.15 + 6,75.10 + 7,25.5} \right) = 6,35\)
Phương sai của mẫu số liệu là:
\({s^2} = \frac{1}{{40}}\left( {5,{{25}^2}.2 + 5,{{75}^2}.8 + 6,{{25}^2}.15 + 6,{{75}^2}.10 + 7,{{25}^2}.5} \right) - 6,{35^2} = 0,2775\)
Độ lệch chuẩn của mẫu số liệu là: \(\sqrt {0,2775} = \frac{{\sqrt {111} }}{{20}} \approx 0,53\)
Bài tập 3.14 trang 86 SGK Toán 12 tập 1 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các bước sau:
Bài toán 3.14 trang 86 SGK Toán 12 tập 1 thường liên quan đến việc tối ưu hóa một đại lượng nào đó, ví dụ như diện tích, thể tích, chi phí, lợi nhuận,… bằng cách sử dụng đạo hàm để tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số biểu diễn đại lượng đó.
Để giải quyết bài toán này, chúng ta cần:
Giả sử bài toán yêu cầu tìm kích thước của một hình chữ nhật có diện tích lớn nhất với chu vi bằng một giá trị cho trước. Chúng ta có thể giải bài toán này bằng cách:
Khi giải bài tập 3.14 trang 86 SGK Toán 12 tập 1 - Kết nối tri thức, cần lưu ý những điều sau:
Để học tập và ôn luyện kiến thức về đạo hàm và ứng dụng của đạo hàm, các em học sinh có thể tham khảo các tài liệu sau:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài tập 3.14 trang 86 SGK Toán 12 tập 1 - Kết nối tri thức một cách hiệu quả.