Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 70, 71 sách giáo khoa Toán 12 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
Vận dụng tọa độ của vectơ trong một số bài toán có liên quan đến thực tiễn
Trả lời câu hỏi Luyện tập 5 trang 76SGK Toán 12 Kết nối tri thức
Với các giả thiết như trong Ví dụ 5, hãy xác định tọa độ của các chiếc máy bay sau 10 phút tiếp theo (tính từ thời điểm máy bay ở điểm B).
Phương pháp giải:
Sử dụng kiến thức về tọa độ của vectơ theo tọa độ hai đầu mút để tìm tọa độ: Trong không gian Oxyz, cho hai điểm \(M\left( {{x_M},{y_M},{z_M}} \right)\) và \(N\left( {{x_N};{y_N};{z_N}} \right)\).
Khi đó, \(\overrightarrow {MN} = \left( {{x_N} - {x_M};{y_N} - {y_M};{z_N} - {z_M}} \right)\).
Lời giải chi tiết:
Gọi D(x; y; z) là vị trí của máy bay sau 10 phút bay tiếp theo (tính từ thời điểm máy bay ở điểm B). Vì hướng của máy bay không đổi nên \(\overrightarrow {AB} \) và \(\overrightarrow {BD} \) cùng hướng. Do vận tốc máy bay không đổi và thời gian bay từ A đến B bằng thời gian bay từ B đến D nên \(AB = BD\). Do đó, \(\overrightarrow {BD} = \overrightarrow {AB} = \left( {140;50;1} \right)\).
Mặt khác: \(\overrightarrow {BD} = \left( {x - 940;y - 550;z - 8} \right)\) nên \(\left\{ \begin{array}{l}x - 940 = 140\\y - 550 = 50\\z - 8 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\;080\\y = 600\\z = 9\end{array} \right.\)
Vậy D(1 080; 600; 9). Vậy tọa độ của máy bay trong 10 phút tiếp theo là (1 080; 600; 9).
Trả lời câu hỏi Luyện tập 7 trang 72 SGK Toán 12 Kết nối tri thức
Trong Ví dụ 7, khinh khí cầu thứ nhất hay thứ hai ở xa điểm xuất phát hơn? Giải thích vì sao.
Phương pháp giải:
Sử dụng kiến thức về tính độ dài của vectơ trong không gian: Trong không gian Oxyz, cho \(A\left( {{x_A};{y_A};{z_A}} \right),B\left( {{x_B};{y_B};{z_B}} \right)\) thì \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \)
Lời giải chi tiết:
Theo Ví dụ 7 ta có, khinh khí cầu thứ nhất có tọa độ là A(2; 1; 0,5), khinh khí cầu thứ hai có tọa độ là \(B\left( { - 1; - 1,5;0,8} \right)\).
Ta có: \(OA = \sqrt {{2^2} + {1^2} + 0,{5^2}} = \frac{{\sqrt {21} }}{2}km\), \(OB = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 1,5} \right)}^2} + 0,{8^2}} = \frac{{\sqrt {389} }}{{10}}km\).
Vì gốc O đặt tại điểm xuất phát và \(OA > OB\) nên khinh khí cầu thứ hai gần điểm xuất phát hơn.
Trả lời câu hỏi Luyện tập 6 trang 71SGK Toán 12 Kết nối tri thức
Trong tình huống mở đầu, hãy tính độ lớn của góc \(\alpha \).
Phương pháp giải:
Sử dụng kiến thức về cosin góc của 2 vectơ trong không gian để tính: Nếu \(\overrightarrow a = \left( {x;y;z} \right)\) và \(\overrightarrow b = \left( {x';y';z'} \right)\) là hai vectơ khác \(\overrightarrow 0 \) thì \(\cos \left( {\overrightarrow a ;\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{xx' + yy' + zz'}}{{\sqrt {{x^2} + {y^2} + {z^2}} .\sqrt {x{'^2} + y{'^2} + z{'^2}} }}\)
Lời giải chi tiết:
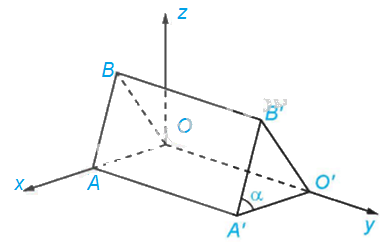
Theo Ví dụ 6 ta có: \(\overrightarrow {A'B'} = \left( { - 120;0;300} \right);\left| {\overrightarrow {A'B'} } \right| = 60\sqrt {29} cm,O'\left( {0;450;0} \right),\)\(A'\left( {240;450;0} \right)\)
Do đó, \(\overrightarrow {A'O'} = \left( { - 240;0;0} \right) \Rightarrow \left| {\overrightarrow {A'O'} } \right| = 240cm\)
Ta có: \(\cos \left( {\overrightarrow {A'B'} ;\overrightarrow {A'O'} } \right) = \frac{{\overrightarrow {A'B'} .\overrightarrow {A'O'} }}{{\left| {\overrightarrow {A'B'} } \right|.\left| {\overrightarrow {A'O'} } \right|}} = \frac{{\left( { - 120} \right)\left( { - 240} \right) + 0.0 + 300.0}}{{60\sqrt {29} .240}} = \frac{{2\sqrt {29} }}{{29}}\)
\( \Rightarrow \widehat {B'A'O'} \approx {68^0}\). Vậy \(\alpha \approx {68^0}\)
Trả lời câu hỏi Luyện tập 5 trang 76SGK Toán 12 Kết nối tri thức
Với các giả thiết như trong Ví dụ 5, hãy xác định tọa độ của các chiếc máy bay sau 10 phút tiếp theo (tính từ thời điểm máy bay ở điểm B).
Phương pháp giải:
Sử dụng kiến thức về tọa độ của vectơ theo tọa độ hai đầu mút để tìm tọa độ: Trong không gian Oxyz, cho hai điểm \(M\left( {{x_M},{y_M},{z_M}} \right)\) và \(N\left( {{x_N};{y_N};{z_N}} \right)\).
Khi đó, \(\overrightarrow {MN} = \left( {{x_N} - {x_M};{y_N} - {y_M};{z_N} - {z_M}} \right)\).
Lời giải chi tiết:
Gọi D(x; y; z) là vị trí của máy bay sau 10 phút bay tiếp theo (tính từ thời điểm máy bay ở điểm B). Vì hướng của máy bay không đổi nên \(\overrightarrow {AB} \) và \(\overrightarrow {BD} \) cùng hướng. Do vận tốc máy bay không đổi và thời gian bay từ A đến B bằng thời gian bay từ B đến D nên \(AB = BD\). Do đó, \(\overrightarrow {BD} = \overrightarrow {AB} = \left( {140;50;1} \right)\).
Mặt khác: \(\overrightarrow {BD} = \left( {x - 940;y - 550;z - 8} \right)\) nên \(\left\{ \begin{array}{l}x - 940 = 140\\y - 550 = 50\\z - 8 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\;080\\y = 600\\z = 9\end{array} \right.\)
Vậy D(1 080; 600; 9). Vậy tọa độ của máy bay trong 10 phút tiếp theo là (1 080; 600; 9).
Trả lời câu hỏi Luyện tập 6 trang 71SGK Toán 12 Kết nối tri thức
Trong tình huống mở đầu, hãy tính độ lớn của góc \(\alpha \).
Phương pháp giải:
Sử dụng kiến thức về cosin góc của 2 vectơ trong không gian để tính: Nếu \(\overrightarrow a = \left( {x;y;z} \right)\) và \(\overrightarrow b = \left( {x';y';z'} \right)\) là hai vectơ khác \(\overrightarrow 0 \) thì \(\cos \left( {\overrightarrow a ;\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{xx' + yy' + zz'}}{{\sqrt {{x^2} + {y^2} + {z^2}} .\sqrt {x{'^2} + y{'^2} + z{'^2}} }}\)
Lời giải chi tiết:
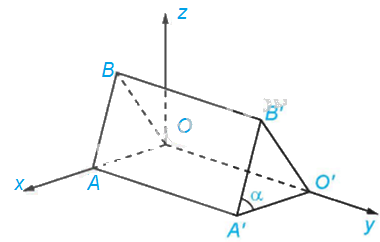
Theo Ví dụ 6 ta có: \(\overrightarrow {A'B'} = \left( { - 120;0;300} \right);\left| {\overrightarrow {A'B'} } \right| = 60\sqrt {29} cm,O'\left( {0;450;0} \right),\)\(A'\left( {240;450;0} \right)\)
Do đó, \(\overrightarrow {A'O'} = \left( { - 240;0;0} \right) \Rightarrow \left| {\overrightarrow {A'O'} } \right| = 240cm\)
Ta có: \(\cos \left( {\overrightarrow {A'B'} ;\overrightarrow {A'O'} } \right) = \frac{{\overrightarrow {A'B'} .\overrightarrow {A'O'} }}{{\left| {\overrightarrow {A'B'} } \right|.\left| {\overrightarrow {A'O'} } \right|}} = \frac{{\left( { - 120} \right)\left( { - 240} \right) + 0.0 + 300.0}}{{60\sqrt {29} .240}} = \frac{{2\sqrt {29} }}{{29}}\)
\( \Rightarrow \widehat {B'A'O'} \approx {68^0}\). Vậy \(\alpha \approx {68^0}\)
Trả lời câu hỏi Luyện tập 7 trang 72 SGK Toán 12 Kết nối tri thức
Trong Ví dụ 7, khinh khí cầu thứ nhất hay thứ hai ở xa điểm xuất phát hơn? Giải thích vì sao.
Phương pháp giải:
Sử dụng kiến thức về tính độ dài của vectơ trong không gian: Trong không gian Oxyz, cho \(A\left( {{x_A};{y_A};{z_A}} \right),B\left( {{x_B};{y_B};{z_B}} \right)\) thì \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \)
Lời giải chi tiết:
Theo Ví dụ 7 ta có, khinh khí cầu thứ nhất có tọa độ là A(2; 1; 0,5), khinh khí cầu thứ hai có tọa độ là \(B\left( { - 1; - 1,5;0,8} \right)\).
Ta có: \(OA = \sqrt {{2^2} + {1^2} + 0,{5^2}} = \frac{{\sqrt {21} }}{2}km\), \(OB = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 1,5} \right)}^2} + 0,{8^2}} = \frac{{\sqrt {389} }}{{10}}km\).
Vì gốc O đặt tại điểm xuất phát và \(OA > OB\) nên khinh khí cầu thứ hai gần điểm xuất phát hơn.
Mục 3 trong SGK Toán 12 tập 1 Kết nối tri thức tập trung vào việc nghiên cứu về đạo hàm của hàm số. Đây là một phần kiến thức nền tảng và quan trọng trong chương trình Toán học lớp 12, đóng vai trò then chốt trong việc giải quyết nhiều bài toán liên quan đến cực trị, đơn điệu và ứng dụng của đạo hàm.
Mục 3 bao gồm các nội dung chính sau:
Để giải tốt các bài tập trong Mục 3, các em cần nắm vững các kiến thức sau:
Bài 1: Tính đạo hàm của các hàm số sau:
f(x) = x3 + 2x2 - 5x + 1
Lời giải: f'(x) = 3x2 + 4x - 5
g(x) = sin(x) + cos(x)
Lời giải: g'(x) = cos(x) - sin(x)
Bài 2: Tìm đạo hàm của hàm số y = (x2 + 1)(x - 2)
Lời giải: y' = (2x)(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
Bài 3: Cho hàm số f(x) = x4 - 4x3 + 6x2 - 4x + 1. Tính f'(x).
Lời giải: f'(x) = 4x3 - 12x2 + 12x - 4
Bài 4: Tìm đạo hàm của hàm số y = √x + 1/x
Lời giải: y' = 1/(2√x) - 1/x2
Đạo hàm có rất nhiều ứng dụng trong giải toán, đặc biệt là trong các bài toán liên quan đến:
Hy vọng với những kiến thức và lời giải chi tiết trên, các em sẽ hiểu rõ hơn về Mục 3 trang 70, 71 SGK Toán 12 tập 1 Kết nối tri thức và tự tin giải quyết các bài tập liên quan. Chúc các em học tập tốt!