Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 20, 21 sách giáo khoa Toán 12 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
Đường tiệm cận ngang
Trả lời câu hỏi Luyện tập 1 trang 21 SGK Toán 12 Kết nối tri thức
Tìm tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x - 1}}{{x - 1}}\).
Phương pháp giải:
Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\).
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 - \frac{1}{x}}}{{1 - \frac{1}{x}}} = 2;\mathop {\lim }\limits_{x \to - \infty } \frac{{2x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{2 - \frac{1}{x}}}{{1 - \frac{1}{x}}} = 2\).
Do đó, tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x - 1}}{{x - 1}}\) là \(y = 2\).
Trả lời câu hỏi Hoạt động 1 trang 20 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{x}\) có đồ thị (C). Với \(x > 0\), xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng \(y = 2\) (H.1.19).
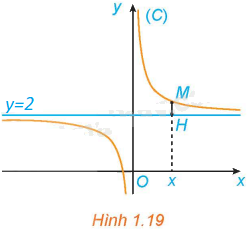
a) Tính khoảng cách MH.
b) Có nhận xét gì về khoảng cách MH khi \(x \to + \infty \)?
Phương pháp giải:
Sử dụng kiến thức về giới hạn của hàm số để tính.
Lời giải chi tiết:
a) Ta có: \(M\left( {x;\frac{{2x + 1}}{x}} \right)\); \(H\left( {x;2} \right)\).
Do đó, \(MH = \sqrt {{{\left( {x - x} \right)}^2} + {{\left( {2 - \frac{{2x + 1}}{x}} \right)}^2}} = \sqrt {{{\left( {\frac{{2x - 2x - 1}}{x}} \right)}^2}} = \frac{1}{x}\) (do \(x > 0\))
b) Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 0\). Do đó, khi \(x \to + \infty \) thì \(MH \to 0\).
Trả lời câu hỏi Vận dụng 1 trang 21 SGK Toán 12 Kết nối tri thức
Giải bài toán trong tình huống mở đầu.
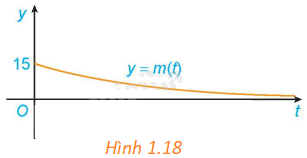
Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số \(m\left( t \right) = 15{e^{ - 0,012t}}\). Khối lượng m(t) thay đổi ra sao khi \(t \to + \infty \)? Điều này thể hiện trên Hình 1.18 như thế nào?
Phương pháp giải:
Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\).
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{t \to + \infty } m\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } 15{e^{ - 0,012t}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{15}}{{{e^{0,012t}}}} = 0\)
Do đó, \(m\left( t \right) \to 0\) khi \(t \to + \infty \).
Trong hình 1.18, khi \(t \to + \infty \) thì m(t) càng gần trục hoành Ot (nhưng không chạm trục Ot).
Trả lời câu hỏi Hoạt động 1 trang 20 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{x}\) có đồ thị (C). Với \(x > 0\), xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng \(y = 2\) (H.1.19).
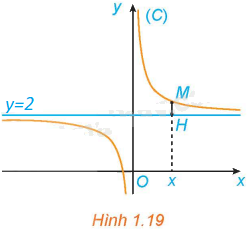
a) Tính khoảng cách MH.
b) Có nhận xét gì về khoảng cách MH khi \(x \to + \infty \)?
Phương pháp giải:
Sử dụng kiến thức về giới hạn của hàm số để tính.
Lời giải chi tiết:
a) Ta có: \(M\left( {x;\frac{{2x + 1}}{x}} \right)\); \(H\left( {x;2} \right)\).
Do đó, \(MH = \sqrt {{{\left( {x - x} \right)}^2} + {{\left( {2 - \frac{{2x + 1}}{x}} \right)}^2}} = \sqrt {{{\left( {\frac{{2x - 2x - 1}}{x}} \right)}^2}} = \frac{1}{x}\) (do \(x > 0\))
b) Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 0\). Do đó, khi \(x \to + \infty \) thì \(MH \to 0\).
Trả lời câu hỏi Luyện tập 1 trang 21 SGK Toán 12 Kết nối tri thức
Tìm tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x - 1}}{{x - 1}}\).
Phương pháp giải:
Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\).
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 - \frac{1}{x}}}{{1 - \frac{1}{x}}} = 2;\mathop {\lim }\limits_{x \to - \infty } \frac{{2x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{2 - \frac{1}{x}}}{{1 - \frac{1}{x}}} = 2\).
Do đó, tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x - 1}}{{x - 1}}\) là \(y = 2\).
Trả lời câu hỏi Vận dụng 1 trang 21 SGK Toán 12 Kết nối tri thức
Giải bài toán trong tình huống mở đầu.
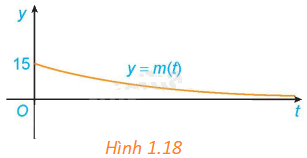
Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số \(m\left( t \right) = 15{e^{ - 0,012t}}\). Khối lượng m(t) thay đổi ra sao khi \(t \to + \infty \)? Điều này thể hiện trên Hình 1.18 như thế nào?
Phương pháp giải:
Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\).
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{t \to + \infty } m\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } 15{e^{ - 0,012t}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{15}}{{{e^{0,012t}}}} = 0\)
Do đó, \(m\left( t \right) \to 0\) khi \(t \to + \infty \).
Trong hình 1.18, khi \(t \to + \infty \) thì m(t) càng gần trục hoành Ot (nhưng không chạm trục Ot).
Mục 1 của chương trình Toán 12 tập 1 Kết nối tri thức tập trung vào việc ôn tập và mở rộng kiến thức về hàm số và đồ thị. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và phân tích.
Bài tập này yêu cầu học sinh ôn lại các kiến thức cơ bản về hàm số bậc hai, bao gồm:
Để giải bài tập này, học sinh cần nắm vững các công thức và định lý liên quan đến hàm số bậc hai. Ngoài ra, học sinh cũng cần rèn luyện kỹ năng vẽ đồ thị hàm số và phân tích các yếu tố ảnh hưởng đến đồ thị.
Bài tập này yêu cầu học sinh ôn lại các kiến thức cơ bản về hàm số mũ và hàm số logarit, bao gồm:
Để giải bài tập này, học sinh cần nắm vững các công thức và định lý liên quan đến hàm số mũ và hàm số logarit. Ngoài ra, học sinh cũng cần rèn luyện kỹ năng vẽ đồ thị hàm số và phân tích các yếu tố ảnh hưởng đến đồ thị.
Bài tập này yêu cầu học sinh vận dụng các kiến thức về hàm số mũ và hàm số logarit để giải quyết các bài toán thực tế, chẳng hạn như:
Để giải bài tập này, học sinh cần hiểu rõ bản chất của các bài toán và vận dụng các công thức phù hợp. Ngoài ra, học sinh cũng cần rèn luyện kỹ năng giải quyết vấn đề và tư duy logic.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 20, 21 SGK Toán 12 tập 1 Kết nối tri thức:
Bài 1: (Giải thích chi tiết từng bước giải, kèm theo hình ảnh minh họa nếu cần thiết)
Bài 2: (Giải thích chi tiết từng bước giải, kèm theo hình ảnh minh họa nếu cần thiết)
Bài 3: (Giải thích chi tiết từng bước giải, kèm theo hình ảnh minh họa nếu cần thiết)
Để giải nhanh các bài tập trong mục này, học sinh có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và rèn luyện kỹ năng, học sinh có thể làm thêm các bài tập sau:
Hy vọng rằng với lời giải chi tiết và các mẹo giải nhanh trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 20, 21 SGK Toán 12 tập 1 Kết nối tri thức. Chúc các em học tập tốt!